Linear Equations
A linear equation is an algebraic equation that forms a straight line when graphed. Each term is either a constant, or the product of a constant and a single variable.
A linear equation can have one or more dependent variables. For example, the following equation expresses the total cost of buying \(a\) apples at $0.50 each and \(b\) bananas for $0.30 each. \( \text{Cost } = a \times $0.50 + b \times $0.30. \) The total cost is dependent, and will vary if \(a\) or \(b\) is changed.
The following concepts must be understood to manipulate and use linear equations: linear rate of change, slope, points, and intercepts. Once these are mastered, they can be used in various ways to define a line when information is missing.
Contents
Linear Rate of Change
A linear rate of change means that the value being discussed changes by a fixed amount in a given unit of time. This means that the slope of the equation will be a constant value and that a graph of the relationship will be a straight line.
When relationships involve a linear rate of change, it is usually simplest to represent them as a linear equation in slope-intercept form:
\[ y = mx+ b. \]
In this formula, \( y \) represents our final amount, \( m \) is the rate of change or the slope of the line, \( x \) is the time elapsed (in the same units as \(m\)), and \( b \) is the amount we started with at time \( x=0\).
Tom makes \($9\) per hour. How much does Tom earn if he works \(20\) hours?
Solution 1:
The amount of money Tom earns can be represented by the equation \[ y = 9x + 0.\] The slope is \( 9\) and the \(y\)-intercept is \(0 \) because Tom earns \($9\) per hour and starts out with \($0.\) Evaluating \( y \) when \( x = 20 \) yields \[ y = 20 \times 9 = 180. \] Thus, Tom earns \($180\) after working \(20\) hours. \(_\square\)Solution 2:
Since Tom earns \($9\) per hour and worked \(20\) hours, we can see that his wages are \[ 20 \times $9 = $180.\ _\square\]
The library loses 100 books every week. If they currently have 10,000 books, how many weeks will it be before they have only 8400 books?
The number of books the library possesses can be expressed as the equation \[ y = -100x + 10000.\] To solve the problem, the value of \( x \) that corresponds to \( y = 8400 \) must be found: \[\begin{align} 8400 &= -100x + 10000 \\ -1600 &= -100x \\ x &= 16 . \end{align}\] Thus, the answer is \(16\) weeks. \(_\square\)
Finding the Slope of a Line
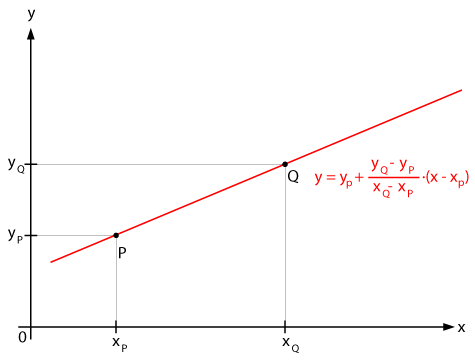
The slope-intercept formula of a line is given by \( y = mx + b, \) where \(m\) and \(b\) are fixed numbers. The set of points satisfying this equation describes a straight line in the \(xy\)-plane.
The slope of a line is the ratio between the change of \(y\) and the change of \(x\). For example, for two different points on a line, \( p_1= (x_1, y_1) \) and \( p_2 = (x_2, y_2) \), the slope is equal to the ratio \( \frac{ y_2 - y_1 } { x_2 - x_1} \). This is also known as the rate of change of \(y\) with respect to \(x\).
Slope is sometimes expressed as rise over run. Students who forget which component is the numerator might want to visualize determining slope as walking up a flight of stairs. The vertical change comes first (is the numerator), and is followed by the horizontal change (the denominator).
For the line \(y=mx+b\), the rate of change of \(y\) with respect to \(x\) is always equal to the slope \(m\) for any pair of distinct points on the line, which can be calculated as follows:
\[ \frac{ y_2 - y_1 } { x_2 - x_1 } = \frac{ (mx_2 + b) - (mx_1 + b) } { x_2 - x_1} = \frac{ m (x_2 - x_1) } { x_2 - x_1} = m. \]
Note: An exception to this rule occurs for lines of the form:
- \( x = k \) for some constant \(k\). In this case, the slope is undefined.
- \( y = k \) for some constant \(k\). In this case, the slope is \(0.\)
By solving the equation of the line when \(x=0\), we obtain \(y = m \cdot 0 + b,\) so \((0,b)\) is a point on the line. Since this point lies on the \(y\)-axis, it is the \(y\)-intercept of the line. This explains the name slope-intercept form for the line \( y = mx + b, \) where \(m\) is the slope and \(b\) is the \(y\)-intercept.
Find the slope and the \(y\)-intercept of the line \( x = 2 y + 6 .\)
At a quick glance, you might be tempted to say the slope of the line is \(2.\) However, the given equation is not in slope-intercept form. In order to convert the equation into slope-intercept form, make \(y\) the subject, which gives \( y = \frac{x}{2} - 3\). Hence, the slope is \( \frac{1}{2} \) and the \(y\)-intercept is \(-3\). \(_\square\)
Let \((a-3)x-y+b-5=0\) be the equation of a line that forms a \(45^\circ\) angle with the positive side of the \(x\)-axis. If the \(y\)-intercept is \(-2,\) what is \(a-b?\)
Rewriting the equation gives:\[\begin{align} (a-3)x-y+b-5&=0\\ y&=(a-3)x+(b-5)\\ a-3&=\tan 45^\circ, \quad b-5=-2\\ a&=4, \quad b=3\\ \Rightarrow a-b&=4-3\\ &=1. \ _\square \end{align}\]
Finding Points on a Line
If we want to find a point on the line, we simply substitute the coordinates into the equation, and solve the resulting linear equation. Typically, we are given either the \(x\)-coordinate, or the \(y\)-coordinate, and asked to find the other. We could also be given the coordinates of the actual point, and asked to determine the slope or \(y\)-intercept.
If the point \(P = (a, 5) \) lies on the line \( y = 3x + 2 \), what is the value of \(a\)?
Substituting the coordinates of the point into the line, \( 5 = 3 \times a + 2 \), which implies \( a = 1 \). \(_\square\)
If the point \( P = (1, 3) \) lies on the line \( y = mx - 4 \), what is the value of \(m\)?
Substituting the coordinates of the point into the line, \( 3 = m \times 1 - 4 \), which implies \( m = 7 \). \(_\square\)
Finding Intercepts of a Line
The \(y\)-intercept is the point where the line crosses the \(y\)-axis. Since the \(y\)-axis corresponds to points which satisfy \( x = 0 \), the \(y\)-intercept is obtained by setting \( x = 0 \), which gives the standard form \( y = m \times 0 + b = b\). The \(y\)-intercept is \( (0, b ) \).
The \(x\)-intercept is the point where the line crosses the \(x\)-axis. Since the \(x\)-axis corresponds to the point that satisfies \( y= 0 \), the \(x\)-intercept is obtained by setting \( y = 0 \), which gives us \( 0 = m \times x + b \), or \( x = - \frac{ b}{m}\).
Note: A common mistake is to switch the definitions of the \(x\)- and \(y\)-intercepts. It can be helpful to draw some examples to ensure the definitions are clear.
What are the \(x\) and \(y\) intercepts of the line \( 2x + 3y = 12 \)?
To find the \(y\)-intercept, we set \( x = 0 \), which give us \( 2 \times 0 + 3 \times y = 12\), or \( y = 4\). Hence, the \(y\)-intercept is \( (0, 4) \).
To find the \(x\)-intercept, set \( y = 0\), which gives \( 2 \times x + 3 \times 0 = 12 \), or \(x = 6 \). Hence, the \(x\)-intercept is \( (6,0) \). \(_\square\)
Linear Equations Word Problems
Sunni has \(300\) bricks on his wall on Monday and \(425\) bricks on his wall on Thursday. If he works at a constant rate every day, how many bricks would we expect him to have on Sunday?
If Sunni is working at a constant rate, the number of bricks will increase linearly. The difference between Thursday and Monday is 3 days, and the difference between \(425\) and \(300\) is \(125,\) making the rate of increase \( \dfrac{125 \text{ bricks}}{3 \text{ days}} \). After another three days, Sunni will have added an additional \(125\) bricks, which makes \( 425 + 125 = 550 \) bricks.Thus, the answer is \(550\) bricks. \(_\square\)
Henry has $125 in his pocket, but he is spending $20 per hour at the arcade. If he leaves in 2.5 hours, how much money will he have left?
Henry's money can be represented by \( y = -20x + 125 \), where \(y\) is the amount of money left and \(x\) is the time (in hours) spent in the arcade. The problem requires evaluating this expression when \( x = 2.5 \), which gives\[ y = -20 (2.5) + 125 = 125-50 = 75. \]
Henry will have \($75\) left when he leaves. \(_\square\)
Linear Equations - Problem Solving
What is the equation of the line that passes through \( (1,5) \) and has a \(y\)-intercept of \(6?\)
Since the slope through \( (1,5) \) and \( (0,6) \) is \( m = \dfrac{5-6}{1-0}=-1 \), and the \(y\)-intercept is 6, the equation of the line is\[ y = -x+6.\ _\square \]
Let \(\sqrt{3}x+ay+b=0\) be the equation of a line passing through the point \((1, 3)\) and forming a \(60^\circ\) angle with the positive side of the \(x\)-axis. What is \(a+b?\)
Rewriting the given equation, we have\[\begin{align} \sqrt{3}x+ay+b&=0\\ y&=-\frac{\sqrt{3}}{a}x-\frac{b}{a} \qquad (1) \\ -\frac{\sqrt{3}}{a}&=\tan 60^\circ\\ &=\sqrt{3}\\ \Rightarrow a&=-1. \end{align}\]
Then \((1)\) becomes \(y=\sqrt{3}x+b.\) Now, substituting in the coordinates \((1, 3)\) gives \(3=\sqrt{3}+b \Rightarrow b=3-\sqrt{3}.\) Therefore,
\[a+b=-1+(3-\sqrt{3})=2-\sqrt{3}.\ _\square \]
What is the length of the line segment that lies in the second quadrant of the \(xy\)-plane and is part of the line passing through the two points \((-3, -1)\) and \((4, 6)?\)
The equation of the line passing through the two points \((-3, -1)\) and \((4, 6)\) is\[\begin{align} y-(-1)&=\frac{6-(-1)}{4-(-3)}(x-(-3))\\ \Rightarrow y&=x+2. \end{align}\]
Now, the \(x\)-intercept of the line is \((-2, 0).\) Similarly, the \(y\)-intercept of the line is \((0, 2).\) Therefore, the length of the line segment that lies in the second quadrant is the length between these two points, which is
\[\sqrt{(0+2)^2+(2-0)^2}=2\sqrt{2}.\ _\square \]
Find all the values of \(k\) such that the three points below lie on a straight line:
\[(2, 0), \quad (6, k-1), \quad (-3+k, 3).\]
Observe that the slope of the line passing through \((2, 0)\) and \((6, k-1)\) is the same as the slope of the line passing through \((6, k-1)\) and \((-3+k, 3).\)
\[\begin{align} \frac{(k-1)-0}{6-2}&=\frac{3-(k-1)}{(-3+k)-6}\\ (k-1)(k-9)&=4(-k+4)\\ k^2-6k-7&=0\\ (k+1)(k-7)&=0. \end{align}\]
Then the values of \(k\) such that \((2, 0), (6, k-1)\) and \((-3+k, 3)\) lie on a straight line are \(k=-1\) and \(k=7.\) \(_\square\)