Linear Time Invariant Systems

Linear time-invariant systems (LTI systems) are a class of systems used in signals and systems that are both linear and time-invariant. Linear systems are systems whose outputs for a linear combination of inputs are the same as a linear combination of individual responses to those inputs. Time-invariant systems are systems where the output does not depend on when an input was applied. These properties make LTI systems easy to represent and understand graphically.

LTI systems are superior to simple state machines for representation because they have more memory. LTI systems, unlike state machines, have a memory of past states and have the ability to predict the future. LTI systems are used to predict long-term behavior in a system. So, they are often used to model systems like power plants. Another important application of LTI systems is electrical circuits. These circuits, made up of inductors, transistors, and resistors, are the basis upon which modern technology is built.

LTI systems are those that are both linear and time-invariant.

Linear systems have the property that the output is linearly related to the input. Changing the input in a linear way will change the output in the same linear way. So if the input $x_1(t)$ produces the output $y_1(t)$ and the input $x_2(t)$ produces the output $y_2(t)$, then linear combinations of those inputs will produce linear combinations of those outputs. The input $\big(x_1(t) + x_2(t)\big)$ will produce the output $\big(y_1(t) + y_2(t)\big)$. Further, the input $\big(a_1 \cdot x_1(t) + a_2 \cdot x_2(t)\big)$ will produce the output $(a_1 \cdot y_1(t) + a_2 \cdot y_2(t))$ for some constants $a_1$ and $a_2$.

In other words, for a system $T$ over time $t$, composed of signals $x_1(t)$ and $x_2(t)$ with outputs $y_1(t)$ and $y_2(t)$,

$$T\big[a_1x_1(t) + a_2x_2(t)\big] = a_1T\big[x_1(t)\big] + a_2T\big[x_2(t)\big] = a_1y_1(t) + a_2y_2(t),$$

where $a_1$ and $a_2$ are constants.

Further, the output of a linear system for an input of 0 is also 0.

Time-invariant systems are systems where the output for a particular input does not change depending on when that input was applied. A time-invariant systems that takes in signal $x(t)$ and produces output $y(t)$ will also, when excited by signal $x(t + \sigma)$, produce the time-shifted output $y(t + \sigma)$.

Thus, the entirety of an LTI system can be described by a single function called its impulse response. This function exists in the time domain of the system. For an arbitrary input, the output of an LTI system is the convolution of the input signal with the system's impulse response.

Conversely, the LTI system can also be described by its transfer function. The transfer function is the Laplace transform of the impulse response. This transformation changes the function from the time domain to the frequency domain. This transformation is important because it turns differential equations into algebraic equations, and turns convolution into multiplication. In the frequency domain, the output is the product of the transfer function with the transformed input. The shift from time to frequency is illustrated in the following image:

Shifting from the time to the frequency domain^[1]

In addition to linear and time-invariant, LTI systems are also memory systems, invertible, casual, real, and stable. That means they have memory, they can be inverted, they depend only on current and past events, they have fully real inputs and outputs, and they produce bounded output for bounded input.

Because of the properties of LTI systems, the general form of an LTI system with output $y[n]$ and input $x[n]$ at time $n$, and constants $c_k$ and $d_j$ is defined a

$$y[n] = c_0y[n-1] + c_1y[n-2] + ... + c_{k-1}y[n-k] + d_0x[n] + d_1x[n-1] + ... + d_jx[n-j] .$$

The state of this system depends on the previous $k$ output values and $j$ input values. Because of the linearity property, the output at time $n$ is just a linear combination of the previous outputs, previous inputs, and current input.

Further, if a string of LTI systems are cascaded together, the output of that new system does not depend on the order in which the systems were cascaded. This property follows from the associative property and the commutative property.

We can take the general form of the LTI system, and write it as an operator equation, and with some manipulation we can turn it into a useful formula:

$$\begin{aligned} Y &= c_0\mathcal{R}Y + c_1\mathcal{R}^2Y + \cdots + c_{k-1}\mathcal{R}^{k}Y + d_0X + d_1\mathcal{R}X + \cdots + d_j\mathcal{R}^jX \\ &= Y\big(c_0\mathcal{R} + c_1\mathcal{R}^2 + \cdots + c_{k-1}\mathcal{R}^{k}\big) + X\big(d_0 + d_1\mathcal{R} + \cdots + d_j\mathcal{R}^j\big). \end{aligned}$$

This is the same equation as

$$Y\big(1 - c_0\mathcal{R} - c_1\mathcal{R}^2 - ... - c_{k-1}\mathcal{R}^{k}\big) = X\big(d_0 + d_1\mathcal{R} + \cdots + d_j\mathcal{R}^j\big) .$$

We can then do some division to create an equation that describes the quotient of the output signal and the input signal:

$$\frac{Y}{X} = \frac{d_0 + d_1\mathcal{R} + \cdots + d_j\mathcal{R}^j}{1 - c_0\mathcal{R} - c_1\mathcal{R}^2 - ... - c_{k-1}\mathcal{R}^{k}} .$$

This is the system function of the LTI system, and it is typically written as the polynomial

$$\frac{Y}{X} = \frac{b_0 + b_1\mathcal{R} + b_2\mathcal{R}^2 + \cdots}{a_0 + a_1\mathcal{R} + a_2\mathcal{R}^2 + \cdots} .$$

Note that both the numerator and the denominator are polynomials in $\mathcal{R}$, the delay variable. Understanding the different roles that the numerator and denominator play is important.

1. In a feedforward system, what will be the value of the denominator in the system function?

Show Answer

A feedforward system has no dependence whatsoever on previous values of $Y$. So, the denominator will be equal to 1.

The impulse response is an especially important property of any LTI system. We can use it to describe an LTI system and predict its output for any input. To understand the impulse response, we need to use the unit impulse signal, one of the signals described in the Signals and Systems wiki. It has many important applications in sampling. The unit impulse signal is simply a signal that produces a signal of 1 at time = 0. It is zero everywhere else. With that in mind, an LTI system's impulse function is defined as follows:

The impulse response for an LTI system is the output, $y(t)$, when the input is the unit impulse signal, $\sigma(t)$. In other words,

$$\mbox{when}\ \ x(t) = \sigma(t) ,\ \ h(t) = y(t) .$$

Essentially, the impulse function for an LTI system basically asks this: If we introduce a unit impulse signal at a certain time, what will be the output of the system at a later time? Sometimes, we can even find the impulse response by doing just that: introducing an impulse signal and seeing what happens.

Convolution is a representation of signals as a linear combination of delayed input signals. In other words, we're just breaking down a signal into the inputs that were used to create it. However, it is used differently between discrete time signals and continuous time signals because of their underlying properties. Discrete time signals are simply linear combinations of discrete impulses, so they can be represented using the convolution sum. Continuous signals, on the other hand, are continuous. Much like calculating the area under the curve of a continuous function, these signals require the convolution integral.

Convolution Sum

$$y[n] = \sum_{k = -\infty}^{\infty}x[k]\, h[n - k]$$

Convolution Integral

$$y(t) = \int_{-\infty}^{\infty}h(\tau)x(t-\tau)\,d\tau = x(t) \ast h(t)$$

Note: $\ast$ is the mathematical convolution symbol.

All LTI systems can be described using this integral or sum, for a suitable function $h()$. $h()$ is the impulse function for the signal. The output of any LTI system can be calculated using the input and the impulse function for that system.

Convolution has many important properties:

1. Commutativity: $x(t) \ast h(t) = h(t) \ast x(t)$
2. Associativity: $\big[x(t) \ast h_1(t)\big] \ast h_2(t) = x(t) \ast \big[h_1(t) \ast h_2(t)\big]$
3. Distributivity of Addition: $x(t) \ast \big[h_1(t) + h_2(t)\big] = x(t) \ast h_1(t) + x(t) \ast h_2(t)$
4. Identity Element: $x(t) \ast h(t) = h(t)$

The transfer function of an LTI system is given by the Laplace transform of the impulse response of the system and it gives valuable information of the system's behavior and can greatly simplify the computation of the output response.

Transfer function

If the impulse response of a system $y(t)$ is given by $h(t)$ then the transfer function of that system is given by $H(S) = \mathcal{L}(h(t))$

The equation describing a causal LTI system is given by: $$\ddot{y(t)} + \dot{y(t)} = x(t)$$

We can compute the impulse response by replacing $x(t)$ with $\sigma(t)$ and solve it using the Laplace transform which will give us:

$$y(t) = h(t) = \mathcal{L}^{-1}(\frac{1}{s^2 + s}) = u(t) - e^{-t}$$

For this differential equation, the transfer function is given by:

$$H(S) = \frac{1}{s^2 + s}$$

We've seen previously that an LTI system can be written as

$$\frac{Y}{X} = \frac{b_0 + b_1\mathcal{R} + b_2\mathcal{R}^2 + \cdots}{a_0 + a_1\mathcal{R} + a_2\mathcal{R}^2 + \cdots} .$$

The transfer function of any (causal) LTI can then be given by:

$$\frac{Y(S)}{X(S)} = \frac{a_0 + a_1\mathcal{S} + a_2\mathcal{S}^2 + \cdots}{b_0 + b_1\mathcal{S} + b_2\mathcal{S}^2 + \cdots} .$$

An LTI system can be represented by:

$$b_n\mathcal{R}^nY + b_{n-1}\mathcal{R}^{n-1}Y \cdots b_0Y = a_m\mathcal{R}^mX + a_{m-1}\mathcal{R}^{m-1}X a_m\mathcal{R}^mX \cdots a_0X$$

Given that $\mathcal{L}\big\{f^{(n)}\big\}=s^n\mathcal{L}\{f\}-\displaystyle\sum_{i=1}^{n}s^{n-i}f^{(i-1)}(0).$ and that in a causal system $f^{(n)}(0) = 0$ , taking the Laplace transform of the previous equation will yield:

$$b_n\mathcal{S}^nY(S) + b_{n-1}\mathcal{S}^{n-1}Y(S) \cdots b_0Y(S) = a_m\mathcal{S}^mX(S) + a_{m-1}\mathcal{S}^{m-1}X(S) a_m\mathcal{S)}^mX(S) \cdots a_0X(S)$$

$$Y(S)(b_n\mathcal{S}^n + b_{n-1}\mathcal{S}^{n-1} \cdots b_0) = X(S)(a_m\mathcal{S}^m + a_{m-1}\mathcal{S}^{m-1} a_m\mathcal{S)}^m \cdots a_0$$

$$\frac{Y(S)}{X(S)} = \frac{a_0 + a_1\mathcal{S} + a_2\mathcal{S}^2 + \cdots}{b_0 + b_1\mathcal{S} + b_2\mathcal{S}^2 + \cdots} .$$

Since $x(t) = \sigma(t)$ and:

$$\mathcal{L}\{\sigma(t)\} = 1$$

$$H(S) = \frac{a_0 + a_1\mathcal{S} + a_2\mathcal{S}^2 + \cdots}{b_0 + b_1\mathcal{S} + b_2\mathcal{S}^2 + \cdots} .$$

Transfer function and the output

We know that the output of an LTI system will be given by the convolution of the signal with the impulse response. Since the convolution in the time domain is equivalent to a multiplication in the Laplace domain, the output $Y(S)$ of a system with the transfer function $H(S)$ to the input $X(S)$ will be given by:

$$Y(S) = H(S)X(S)$$

One can easily calculate the output in the time domain by $y(t) = \mathcal{L}^{-1}(Y(S))$

What is the output of the system described by $\ddot{y(t)} + \dot{y(t)} = x(t)$ when $x(t) = e^t$?

We know from previously that: $$H(S) = \frac{1}{s^2 + s}$$

Since $X(S) = \mathcal{L}\{x(t)\} = \frac{1}{S-1}$, so: $$Y(S) = X(S)H(S) = \frac{1}{S(S+1)(S-1)}$$

The output is then given by: $$y(t) = \mathcal{L}^{-1}\{Y(S)\} = \mathcal{L}^{-1}\{\frac{1}{S(S+1)(S-1)}\} = 0.5e^{t} + 0.5e^{-t} - u(t)$$

Poles and Zeros

Since the transfer function is described by the division of two polinomials, we can factor those polinomials into:

$$H(S) = \frac{(S + z_0)(S + z_1)(S + z_2)\cdots}{(S + p_0)(S + p_1)(S + p_2)\cdots}$$

Where $z_0, z_1, z_2 \cdots$ are the complex zeros of the system and $p_0, p_1, p_2 \cdots$ are the complex poles. They give interesting information on the system's behaviour and can be seing in more detailed on the wiki Predicting System Behavior.

Discrete time signals are simply a collection of individual signals. These discrete signals can be a product of sampling a continuous time signal, or it can be a product of truly discrete phenomena. These discrete signals can be represented in a graph with individual points connected to the $x$-axis, as in the graphic below.

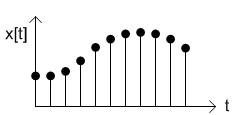Discrete Time Signal^[2]

Here, time is on the $x$-axis and the signal is on the $y$-axis. It is discretized, meaning the signal function is not continuous. So, as mentioned earlier, a sum is needed to calculate its output at any given time.

We have a discrete LTI system. Given the following input function and impulse response function, calculate the output of the system at time $n$. Note that $u[n]$ is the unit step function.

Solve for $x[n] \ast h[n]$:

$$\begin{aligned} u[n] &= \begin{cases} 1 & \mbox{if } n \geq 0 \\ 0 & \mbox{if } n \lt 0\end{cases}\\ x[n] &= u[n] \\ h[n] &= 2^nu[n]. \end{aligned}$$

Show Answer

We have

$$y[n] = \sum_{k=-\infty}^{\infty}x[k]\, h[n-k] = \sum_{k=-\infty}^{\infty}u[k]2^{n-k}u[n-k] = 2^n\sum_{k=-\infty}^{\infty}2^{-k}u[k]\, u[n-k] .$$

Now, we need to analyze the limits of this sum. When $k \lt 0$, $x[k]\, k[n-k] = 0$, so we can ignore any value of $k$ that is less than 0. When $k \geq 0$, the two functions overlap only in the range $\{0, n\}.$ So, those are the limits we need to use. Therefore, the equation reduces to

$$\begin{aligned} y[n] &= 2^n\sum_{k=0}^{n}2^{-k} \\ &= 2^n\frac{1 - \frac{1}{2}^{n+1}}{1-\frac{1}{2}} \\ &= \frac{1 - 2^{n+1}}{1 - 2} \\ &= 2^{n+1} - 1.\ _\square \end{aligned}$$

Continuous LTI systems have signals that are defined at all possible time values. So, we need to use integrals to properly understand this type of system.

Let's say that we have an LTI system with an impulse response function $h(t)$. We want to figure out how an input, $x(t)$, will affect this system. To do so, we need convolution! Assume for this problem that $t$ is greater than zero (if it wasn't, the answer would always be zero!).

Try convolving the following two functions. Solve for $x(t) \ast h(t)$. $u(t)$ is the unit step function:

$$\begin{aligned} u(t) &= \begin{cases} 1 & \mbox{if } t \geq 0 \\ 0 & \mbox{if } t \lt 0\end{cases}\\ x(t) &= u(t) \\ h(t) &= e^{-3t}u(t). \end{aligned}$$

Show Answer

So, $x(t) \ast h(t)$ is equal to

$$\int_{-\infty}^{\infty}h(\tau)u(t - \tau)\, d\tau.$$

To understand these integral bounds, it's useful to think about the functions and where there are non-zero. $h(\tau)$ is zero to the left of the $y$-axis, or for all negative numbers. $u(t - \tau)$ is zero for all values greater than $\tau$. So, our bounds are $\{0, \tau\}.$ The inside of our integral is the product of two signals, and we're really just calculating the area under the curve. So, now we have

$$\int_{0}^{t}e^{-3\tau}d\tau = \frac{1}{-3}\left. e^{-3\tau} \right|^{t}_{0} = \frac{1}{-3}\left[e^{-3t} - 1\right].\ _\square$$

1. Calvert, J. Time and Frequency Domains. Retrieved April 10, 2016, from http://mysite.du.edu/~etuttle/electron/elect6.htm
2. Ho Ahn, S. Feedforward. Retrieved June 16, 2016, from http://www.songho.ca/dsp/signal/signals.html