Lists
A list is an abstract data type used for storing sequential items. They are an important concept in the Lisp family of programming languages and in functional programming languages in general. It's more common to use arrays, queues, and stacks for similar tasks in imperative languages.
Contents
Characteristics of a List
The power of lists comes from their definition of head and tail:
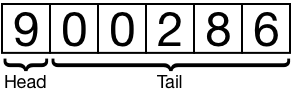
The head is the first item in the list; the tail is all remaining items. The tail is itself a list, having its own head and tail:

This can be repeated for every tail:
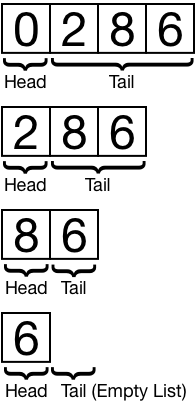
Exploiting this property allows for operations to be defined on lists using recursion with minimal code.
Minimal Required Functionalities
Function Name* \(\hspace{15mm}\) Provided Functionality newCreates an empty list. appendAdds an item to the end of the list. prependAdds an item to the beginning of the list. headReturns the item at the beginning of the list. tailReturns all items except the head. If the list only has 1 item, returns an empty list. is_emptyReturns a bool indicating whether or not the list contains any items. *Exact names are not required. In fact, some functionality may be provided by a given language directly via special syntax.
Sample Python Implementation Using a Linked List
Note that Python has a built-in type that it calls list. It doesn't specifically define the required API to be used as a list ADT (abstract data type), but it does provide built-in syntax for array slicing. Since the tail function of the list ADT could be considered a specific case of slicing, the argument could be made that the Python list does fulfill the requirements of the list ADT API in a roundabout fashion.
This sample implements a linked list in an object-oriented style and includes the minimum functionality of a list ADT. The list class only has a reference to the head node, so the append operation has to walk through all the nodes to find the last node, making it an \(O(n)\) operation.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | |
Try out append and prepend:
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
1 2 3 4 5 6 | |
Now try out head and tail:
1 2 | |
1 2 | |
Example: Summing All Values in a List
Using the Python implementation from above:
def sum_list(the_list): if not the_list.is_empty(): return the_list.head() + sum_list(the_list.tail()) else: return 0 some_numbers = List() some_numbers.prepend(3) some_numbers.prepend(3) some_numbers.prepend(4) some_numbers.prepend(1) some_numbers.prepend(7) some_numbers.prepend(7) some_numbers.prepend(1) some_numbers.prepend(4) some_numbers.prepend(5) some_numbers.prepend(7) print(sum_list(some_numbers))
142
Using the Haskell built-in list:
sumList :: (Num a) => [a] -> a sumList [] = 0 sumList x = head x + sumList(tail x) main = print(sumList [7,5,4,1,7,7,1,4,3,3])
142
Example: Implement Right Fold
Generalizing upon the previous example, a right fold takes any arbitrary function and cumulatively applies it to the entire list.
Using the Python implementation from above:
def special_add(x, y): return x + 2 * y # specifically, this is a right fold def fold_list(the_function, the_list): if the_list.tail().is_empty(): return the_list.head() else: return the_function(the_list.head(), fold_list(the_function, the_list.tail())) some_numbers = List() some_numbers.prepend(3) some_numbers.prepend(3) some_numbers.prepend(4) some_numbers.prepend(1) some_numbers.prepend(7) some_numbers.prepend(7) some_numbers.prepend(1) some_numbers.prepend(4) some_numbers.prepend(5) some_numbers.prepend(7) print(fold_list(special_add, some_numbers))
13257
Using the Haskell built-in list:
specialAdd :: (Num a) => a -> a -> a specialAdd x y = x + 2 * y -- specifically, this is a right fold foldList :: (a -> a -> a) -> [a] -> a foldList f [x] = x foldList f l = f (head l) (foldList f (tail l)) main = print(foldList specialAdd [7,5,4,1,7,7,1,4,3,3])
13257
Try It Yourself: Implement Map
Map is a function which takes another function and applies it to each item in a list, returning the new list.
1 2 3 | |
Using only head and tail as defined by the List ADT, implement map.
Use your implementation of map to apply the function
1 2 | |
to the list \([32, 57, 16, 8, 38]\).