Queues
Queues are abstract data types that, like the stack, have restrictions on where elements can be added or removed. These restrictions mandate FIFO (first-In, first-out) removal of elements, and that the order of elements in the line be retained.
One can think of a queue like a cafeteria line: the person at the front is served first, and people are added to the line at the back. Thus, the first person to enter the queue is the first to be served, and the most recent person to enter the queue is served after everyone else (FIFO).
In queues, a main focus is on the head, where elements are removed, and the tail of the queue, where they are added.
Contents
Minimal Required Functionalities
There are two basic operations related to the queue:
Function Name* Provided Functionality enqueue(i)Insert element i at the tail of the queue. dequeue()Remove the element at the head of the queue. Additionally, queues are often implemented with the following operations to save computation:
Function Name* Provided Functionality size()returns the current size of the queue peek()returns the element at the head of the queue without changing the queue *Exact names are not required. In fact, some functionality may be provided by a given language directly via special syntax.
Sample Python Implementation Using a List
The following is an implementation of a queue in Python. This implementation uses a Python list as its data structure.
Here, the head is at the lowest possible index of the array (on the left), and the tail is at the highest possible index (on the right).
Note: Queues are already implemented for you in Python using their list type and a few functions. This is a re-implementation.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | |
Example: Adding and Removing Items in a Queue
The following demonstration uses the above implementation of a queue using Python.
Instantiating the queue:
>>> queue = Queue()
>>> queue.size()
0
Adding three people to the queue:
>>> queue.enqueue('Alice')
>>> queue.enqueue('Bob')
>>> queue.enqueue('Charlie')
>>> queue.size()
3
The queue currently looks like this (remember, the head is on the left):
>>> queue.qlist
['Alice', 'Bob', 'Charlie']
Dequeueing the queue:
>>> queue.dequeue()
'Alice'
>>> queue.qlist
['Bob', 'Charlie']
>>> queue.dequeue()
'Bob'
>>> queue.qlist
['Charlie']
>>> queue.dequeue()
'Charlie'
>>>queue.qlist
[]
Now the queue is empty and no dequeueing or peeking can be done:
>>> queue.dequeue()
queue underflow
>>> queue.peek()
queue is empty
Time Complexity
The time complexity of queues depends on the type of the data structure used and the specific implementation built. Below is the complexity analysis of some data structures and their enqueues and their dequeues:
\[\begin{array} &&\text{Linked list queue enqueue - O(1),} &\text{Array queue enqueue - O(1),} \\ &\text{Linked list queue dequeue - O(1),} &\text{Array queue dequeue - O(n).}\end{array}\]
Although the concept may be simple, programming a queue isn't as simple as programming a stack. The cafeteria line example again serves to explain why a linked list is much faster than an array when it comes to dequeueing:
One person leaves the cafeteria line. Everyone behind this person must step forward. In an array, this process happens one at a time, only one person can move at a time. The first person leaves. Then the second person steps forward to fill the space left by the first person, then the third person steps forward to fill the space left by the second person, and so on. The line will move very slowly indeed.
In the best and worst case scenario, every single person has to move forward by 1. This takes \(\text{O(n)}\) time because the number of movements depends on the number of people in line.
However, in the case of the linked list, only 1 person has to move. This would be like a cafeteria line where the order taker steps forward, not the whole line itself. Once the linked list dequeues the person at the front of the line, the next person becomes the new front of the line. They, and the rest of the people in line, do not have to step forward. Because this operation does not depend on how big the line is, it takes \(\text{O(1)},\) or constant, time.
Example Question
Consider a line of 10 people waiting to buy food at a fast food restaurant. Imagine this line is represented by a queue.
- Where is the head of this queue, the person in front or the person in the back?
- If the person in front buys their food and leaves, how many people need to move (not including the person who left)?
- Is this O(n) time or O(1) time? Is this queue implemented using an array or a linked list?
A1. The head of the queue is the person at the front of the line.
A2. 9 people have to move (10 people minus the 1 who left).
A3. This is O(n) time because it is dependent on the number of people in the line (in this case, 10). This queue is implemented using an array.
Standard Applications
Queues are most often used to implement a list in such a way that items can be retrieved in the same order in which they arrive. They offer a lot of practical applications in various fields, such as in operating systems, mail services, CPU scheduling, elevators, and keyboard buffering.
Queues are very useful in networks, especially for the Internet. For example, when you send two texts to the same person, your phone might say "Sending 1 of 2." The network has used a queue to store your texts so that they arrive in the same order you sent them. Or, when you send data to a website, you want to make sure that the data gets there in the right order. So, the website has a queue where it collects your data as it waits for it to be processed.
Circular Queues
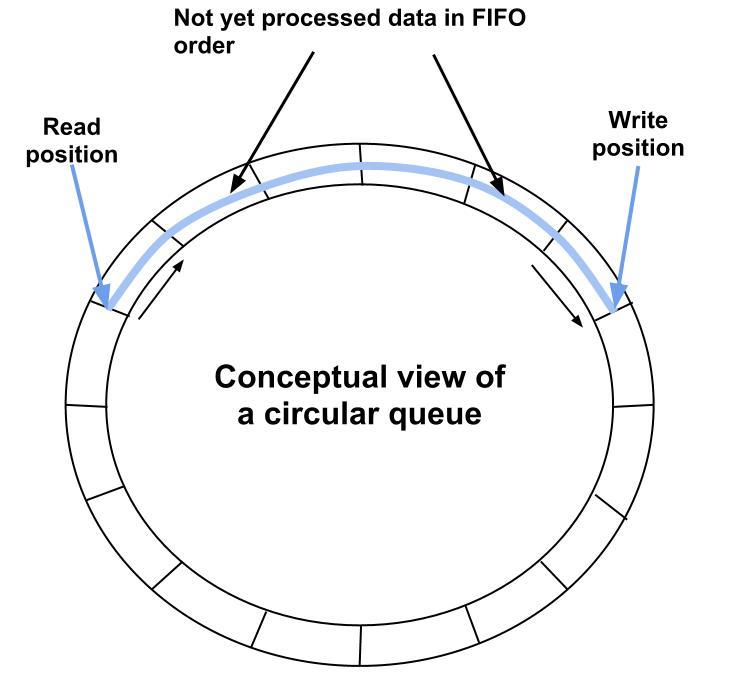 Circular Queue
Circular Queue
There are a couple of basic ways to implement a queue. The first is to just make an array and shift all the elements to accommodate enqueues and dequeues. This, as we saw above, is slow.
The slowness of the previous method is that with many elements, the shifting takes time. Thus another method to implement queues is to shift the enqueue and dequeue points. In the aforementioned cafeteria line example, if the line continually moves backward as each person leaves the line, then the people don't need to step forward or backward, thereby saving time.
However, this introduces one important invariant for circular queues--they must have a maximum capacity! Otherwise, there would be no way of knowing if you've reached the end of the queue, and the benefit would be lost.
In this implementation, placeholders are used in the queue. This is so that the queue does not lose its place if it were to empty itself in the middle. This also uses a list as its data structure. The following code demonstrates the usage of circular queues:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | |
To understand this circular implementation, think of the array as a circle. When an element is dequeued, the queue doesn't shift all of the elements forward to the start of the queue. Instead, the class shifts the start of the queue back. Eventually, the start of the queue will have shifted so far that the queue will extend beyond the end of the array. This is where the circle comes in. When the queue reaches the end of the array, it wraps around to the beginning of the array. We do this wrapping by using modulo math on the head and the tail of the queue.