Merkle Tree
A Merkle tree is a hash-based data structure that is a generalization of the hash list. It is a tree structure in which each leaf node is a hash of a block of data, and each non-leaf node is a hash of its children. Typically, Merkle trees have a branching factor of 2, meaning that each node has up to 2 children.
Merkle trees are used in distributed systems for efficient data verification. They are efficient because they use hashes instead of full files. Hashes are ways of encoding files that are much smaller than the actual file itself. Currently, their main uses are in peer-to-peer networks such as Tor, Bitcoin, and Git.
Overview
Merkle trees are typically implemented as binary trees, as shown in the following image. However, a Merkle tree can be created as an \(n\)-nary tree, with \(n\) children per node.
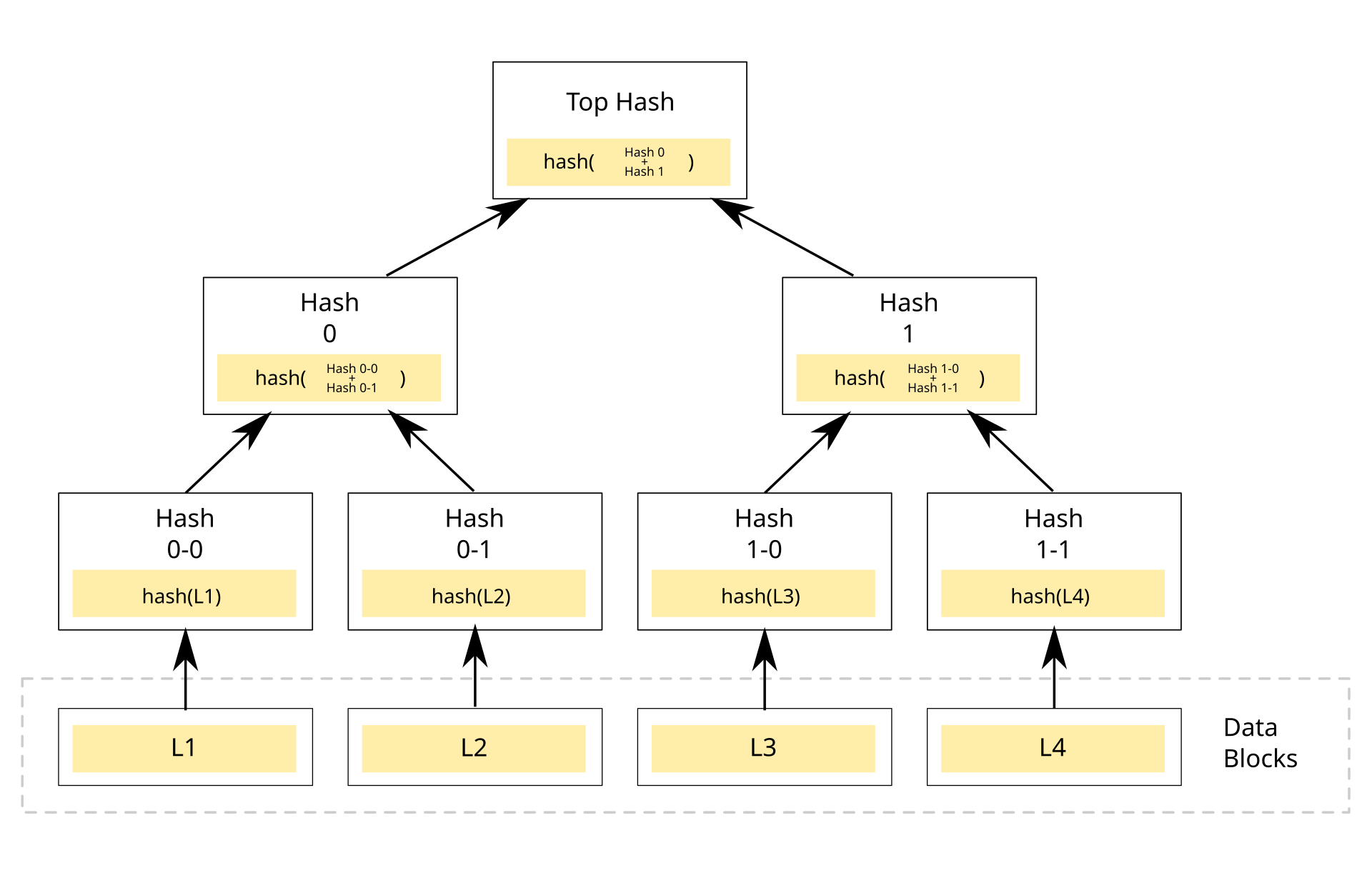 Binary Merkle Tree [1]
Binary Merkle Tree [1]
In this image, we see an input of data broken up into blocks labeled L1 though L4. Each of these blocks are hashed using some hash function. Then each pair of nodes are recursively hashed until we reach the root node, which is a hash of all nodes below it.
Benefits and Protocol
In various distributed and peer-to-peer systems, data verification is very important. This is because the same data exists in multiple locations. So, if a piece of data is changed in one location, it's important that data is changed everywhere. Data verification is used to make sure data is the same everywhere.
However, it is time-consuming and computationally expensive to check the entirety of each file whenever a system wants to verify data. So, this is why Merkle trees are used. Basically, we want to limit the amount of data being sent over a network (like the Internet) as much as possible. So, instead of sending an entire file over the network, we just send a hash of the file to see if it matches. The protocol goes like this:
- Computer A sends a hash of the file to computer B.
- Computer B checks that hash against the root of the Merkle tree.
- If there is no difference, we're done! Otherwise, go to step 4.
- If there is a difference in a single hash, computer B will request the roots of the two subtrees of that hash.
- Computer A creates the necessary hashes and sends them back to computer B.
- Repeat steps 4 and 5 until you've found the data blocks(s) that are inconsistent. It's possible to find more than one data block that is wrong because there might be more than one error in the data.
Note that each time a hash is found to match, we need \(n\) more comparisons at the next level, where \(n\) is the branching factor of the tree.
This algorithm is predicated on the assumption that network I/O takes longer than local I/O to perform hashes. This is especially true because computers can run in parallel, calculating multiple hashes at once.
Because the computers are only sending hashes over the network (not the entire file), this process can go very quickly. Plus, if an inconsistent piece of data is found, it's much easier to insert a small chunk of fixed data than to completely rewrite the entire file to fix the issue.
The reason that Merkle trees are useful in distributed systems is that it is inefficient to check the entirety of file to check for issues. The reason that Merkle trees are useful in peer-to-peer systems is that they help you verify information, even if some of it come from an untrusted source (which is a concern in peer-to-peer systems).
The way that Merkle trees can be helpful in a peer-to-peer system has to do with trust. Before you download a file from a peer-to-peer source—like Tor—the root hash is obtained from a trusted source. After that, you can obtain lower nodes of the Merkle tree from untrusted peers. All of these nodes exist in the same tree-like structure described above, and they all are partial representations of the same data. The nodes from untrusted sources are checked against the trusted hash. If they match the trusted source (meaning they fit into the same Merkle tree), they are accepted and the process continues. If they are no good, they are discarded and searched for again from a different source.
Use Cases
As stated above, Merkle trees are especially useful in distributed, peer-to-peer systems where the same data should exist in multiple places. These systems use Merkle trees or variants on the Merkle tree in their implementation.
Git is a popular version control system mainly used by programmers. All of the saved files are saved on every user's computer at all times. So, it's very important to check that these changes are consistent across everyone's computer.
Bitcoin is a popular online, anonymous currency. All transactions in bitcoin are stored in blocks on what is called the blockchain. This blockchain exists on every bitcoin user's computer. Leaves of the Merkle tree used in bitcoin are typically hashes of single blocks. Every time someone wants to alter the blockchain (for example by adding transactions), this change needs to be reflected everywhere.
Merkle trees can be used to check for inconsitencies in more than just files and basic data structures like the blockchain. Apache Cassandra and other NoSQL systems use Merkle trees to detect inconsistencies between replicas of entire databases. Imagine a website that people use all over the world. That website probably needs databases and servers all over the world so that load times are good. If one of those databases gets altered, then every single other database needs to be altered in the same way. Hashes can be made of chunks of the databases, and Merkle trees can detect inconsistencies.
Complexity
Merkle trees have very little overhead when compared with hash lists. Binary Merkle trees, like the one pictured above, operate similarly to binary search trees in that their depth is bounded by their branching factor, 2. Included below is worst-case analysis for a Merkle tree with a branching factor of \(k\).
| Average | Worst | |
| Space | \(O(n)\) | \(O(n)\) |
| Search | \(O\big(\log_2(n)\big)\) | \(O\big(\log_k(n)\big)\) |
| Traversal | *\(O(n)\) | *\(O(n)\) |
| Insert | \(O\big(\log_2(n)\big)\) | \(O\big(\log_k(n)\big)\) |
| Delete | \(O\big(\log_2(n)\big)\) | \(O\big(\log_k(n)\big)\) |
However, a very important aspect of Merkle trees (and their biggest use case) is in the synchronization of data. In the typical case, this synchronization will be a \(\log_2(n)\) operation because it is based on traversal and search. However, there is a worst-case situation where there are no nodes in common. In this scenario, synchronization is akin to making a complete copy of the file, which will be a \(O(n)\) operation.
| Average | Worst | |
| Synchronization | \(O\big(\log_2(n)\big)\) | \(O(n)\) |
References
- zaghal, A. Wikipedia Merkle Tree. Retrieved April 27, 2016, from https://en.wikipedia.org/wiki/Merkle_tree