This wiki shows the first problem of the Open Problems Group, sometimes called Knights and Kings. There is currently no known answer to the question. Feel free to add results here!

This is an open question. There is currently no known answer.

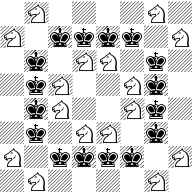
On a chessboard of any size, is there a configuration of kings and knights such that each king attacks exactly 2 kings and 2 knights, and each knight attacks exactly 2 kings and 2 knights?

(Sub-problem -- if it is possible, what's the smallest board needed?)

Source.

Details: Kings can attack any adjacent square, including diagonally. Knights move in an L shape as shown below.

From João Areias:

We know that we can divide the board into 2x2 boards. All the possible configurations for Kings on 2x2 boards are shown below, ignoring rotations and reflections: \(\)

• 1
• 2
• 3
• 4
• 5

Now, we can discard the configuration 5 since all the kings are attacking 3 other kings. Configuration 4 is already complete by itself, all the kings are attacking 2 other kings, it is one solution as well as combining it with other solutions such that no king on this configuration attacks a king on the other solution is also a solution. Configuration 1 will only form a solution if connected with the others such that the king is adjacent to another king, which can be broken down on one of the other configurations as shown in the following image: \(\)

Configuration 1 \(\)

The other two configurations, 2 and 3, are a bit more interesting. On both of them, there are 2 kings that each needs to attack 1 more king. One can concatenate another of those pieces to make it attack another of those kings, this will satisfy the conditions to one of the previous kings and one of the added kings, leaving us in the same situation as before. The only way to satisfy the conditions for all kings one a finite board then is if the added piece attacks the previous pieces on 2 different points closing a loop like the images shown here : \(\)

• 2x2
• 3x3
• 4x3
• 4x4
• 5x5
• 6x5
• 6x6
• 8x7

One condition I found is that for any 2x2 grid on your pattern, the configuration 4 cannot appear on the loop, for example, loop 1 is invalid. \(\)

loop

Here another more complicated pattern just following these rules. \(\)

pattern

From Jon Haussmann:

From Novak Radivojević:

pattern No.1 pattern No.2 pattern No.3

From Andrew Wang:

From Stefan van der Waal:

If some smallest, finite board exists that fulfils the requirements, we know the following of that board:

• The board has edges
• Every edge has at least one piece on it

In the boards, I’m going to use black pawns to mark squares that have to be empty, and white pawns to mark squares that need to have either a king or a knight, but it’s not yet clear which of the two.

The piece on the edge can be either a king, or a knight, which means at least one of the following 20 formations (or a vertical reflection of one of those) has to be somewhere on the board:

- King 1 (impossible) - King 2 (impossible) - King 3 (impossible) - King 4 (impossible) - King 5 (impossible) - King 6 (impossible) - King 7 (still plausible) - King 8 (still plausible) - King 9 (impossible) - King 10 (still plausible) - King 11 (still plausible) - King 12 (impossible) - King 13 (impossible) - King 14 (impossible) - King 15 (impossible) - King 16 (still plausible) - Knight 1 (still plausible) - Knight 2 (still plausible) - Knight 3 (still plausible) - Knight 4 (still plausible)

If it’s possible to prove all of these 20 formations are impossible, it’s proven no piece can be on the edge. That would contradict the idea a finite, smallest board exists, which in turn would prove there is no finite, valid board.

So far I’ve been able to prove that 11 of these 20 formations are impossible. I tried to prove the others to be impossible as well, but I was unable to do it. I suspect there's no short and simple proof for any of those.

Below are the proofs why the other 11 formations are impossible. All of these boards only have an edge on the left. The edges on the top, right, and bottom are only there to make the images fit on the screen.

The king on a6 already attacks 3 pieces, so the fourth piece it will attack has to be on either a7 or b7. The king on b6 also already attacks 3 pieces. We also know one more piece has to be on either a7 or b7, so c7, c6, and c5 all have to be empty. The piece that has to go on either a7 or b7 is a knight. It can’t go on a7, because it would then attack the squares b5, c6, c8, and b9. But c6 is empty. Therefore a7 has to be empty, and b7 needs to have the knight. The knight on b5 now attacks only 4 non-empty squares, so a3, c3, d4, and d6 all need to have some piece. Let’s look at square c4. If it has a knight, it would attack 2 knights and the unknown pieces on a3 and d6, so those two need to be knights. But if that’s the case the knight on d6 would attack 3 knights: b7, b5, and c3. Therefore c4 isn’t allowed to have a knight.

Then how about a king? That king would then attack 2 knights, and the unknown pieces on c3 and d4. D3 and d5 would then have to be empty. However, the knight on b4 would then only be able to attack 3 non-empty squares. Therefore c4 has to be empty.

If the unknown piece on a3 would be a knight, it would attack 3 non-empty squares, so it has to be a king. That king on a3 attacks only 4 non-empty squares, so a2, b2, and b3 need to have 2 kings and 1 knight on them. The piece on b3 isn’t allowed to be one of the kings because it would then attack 5 pieces. Therefore the knight has to go on b3, and a2 and b2 are kings. We’ve now reached a contradiction. The king on b2 attacks 4 pieces, so a1 and b1 have to be empty. However, the king on a2 is only attacking 3 pieces, so either a1 or b1 needs to have a knight. Therefore the formation king 1 isn’t allowed.

The knight on a3 attacks only 4 squares, so c4, c2, and b1 need to have some piece. The king on b5 now attacks 4 pieces, so a6 and b6 have to be empty. However, the king on a5 needs a knight on either a6 or b6. Therefore formation king 2 isn’t allowed.

The king on a5 attacks 4 non-empty squares, so a6 and b6 have to be knights. The king on b5 now attacks 4 shapes, so c4, c5, and c6 have to be empty. However, the knight on a3 needs to attack some shape on c4. Therefore formation king 3 isn’t allowed.

The king on b3 already attacks 4 shapes, so c4, c3, and c2 have to be empty. The king on a4 already attacks 2 kings and 1 knight, so the last knight has to go on either a5 or b5. On a5 that knight would only attack 3 non-empty squares, so the knight has to go on b5. Now look closely at the area a5, b5, a4, b4, a3, b3. It’s the vertical reflection of the formation king 1, and we’ve already proven above that the formation king 1 isn’t allowed, so king 4 also isn’t allowed. (can somebody give me feedback on the rigorousness of this argument? It makes sense in my head, but I’m not sure if it’s rigorous enough)

The king on b3 already attacks 4 shapes, so c4, c3, and c2 have to be empty. However, the knight on a2 has to attack some shape on c3. Therefore the formation king 5 isn’t allowed.

The knight on a2 can only attack 3 non-empty squares. Therefore formation king 6 isn’t allowed.

The knight on a2 can only attack 3 non-empty squares. Therefore formation king 9 isn’t allowed.

The king on b3 already attacks 4 shapes, so c4, c3, and c2 have to be empty. However, the knight on a2 needs c3 to have some shape. Therefore king 12 is not allowed.

The king on b3 already attacks 4 shapes, so c4, c3, and c2 have to be empty. However, the knight on a4 needs c3 to have some shape. Therefore king 13 is not allowed.

The king on b3 already attacks 4 shapes, so c4, c3, and c2 have to be empty. However, the knight on a2 needs c3 to have some shape. Therefore king 14 is not allowed.

The knight on a2 needs to attack both c3 and c1. However, the king on b2 already attacks 3 shapes, so either c3 or c1 needs to be empty.

Below is an image of the corner of a chessboard.

If a finite chessboard exists, the squares with a 1, 2, 3, and 4 have to be empty. Below are the proofs.

Square 1 isn't allowed to have a knight, because a knight would attack only 2 squares, which is less than the minimum of 4 that's required.

Square 1 also can't have a king, because a king on square 1 would attack only 3 squares, which is less than the minimum of 4 that's required.

Since square 1 can have neither a knight, nor a king, it has to be empty.

Every knight must attack at least 4 squares to attack 2 kings, and 2 knight, so square 2 isn’t allowed to have a knight.

To figure out if a king may go in the square, assume it does and extrapolate that decision until either a complete board is created that satisfies the conditions, or a contradiction is detected.

The king attacks 5 squares, and exactly 2 of those squares must be knights and 2 must be kings.

Square a8 has to be empty, as explained above under 'Square 1'.

Square b8 isn’t allowed to have a knight for the same reason a7 wasn’t allowed to have a knight, so it has to have a king. We now have the following setup (I use black pawns to visualize which squares have to be empty):

We now need to place 1 more king and 2 knight in the squares b7, a6, and b6. There are three ways to do that.

1: Place the king on b7

This formation isn’t possible. The king on b7 already attacks 2 kings and 2 knights. Therefore c7 has to be empty. However, the knight on a6 attacks only 4 squares, including c7, which means c7 is not allowed to be empty.

2: Place the king on b6

This formation also isn’t possible. The knight on a6 attacks 4 squares, including c7 and c5, so both squares need to have a piece. However, the king on b6 already attacks 3 pieces, so at least 1 of the squares c7 and c5 has to be empty.

3: Place the king on a6

The king on b8 has to attack one more king, and one more knight. Using the same logic we used at #2: Place the king on b6, we can deduce that the king has to go on c8, and the knight on c7.

The knight on b7 attacks only 4 squares, so a5, c5, d6, and d8 all must have some piece (I use white pawns to visualize squares that must have either a king or a knight, but it’s not yet clear which of the two it is).

The king on a6 already attacks 1 king and 2 knights, so a5 has to be a king, and b5 has to be empty. Similar logic is used to determine d8 must have a king, and d7 has to be empty. The knight on b7 now attacks 2 kings, so the remaining 2 squares it attacks should both be knights.

The kings on a5 and d8 already attack 1 king, 1 knight, and 1 empty square, so a4, b4, e8, and e7 must all have some piece. The knight on b6 attacks 1 king, 1 empty square, and 3 other squares, so d5 and c4 have to have some piece as well. Similar logic with the knight on c7 can get used to prove e6 must have some piece.

The knights on c5 and d6 now attack 4 pieces, so the squares f7, f5, e4, d3, and b3 have to be empty.

The squares a4, and e8 can no longer be kings, because those would attack only 3 squares. Therefore a4, and e8 have to be knights, and b4, and e7 have to be kings.

The kings on b4 and e7 now attack 1 king, 2 knights, and 1 unknown piece, so the squares c4, and e6 have to be kings, and the squares a3, c3, f6, and f8 have to be empty.

We’ve now reached a contradiction. The knight on a4 attacks only 4 squares, so c3 has to have some piece. However, that square is currently empty. Therefore our initial assumption that a king on a7 was a valid start was false.

Since a knight is not allowed to go on a7, and placing a king on a7 will result in a contradiction, the square next to the corner has to be empty. Therefore the correct answer is 'The square can neither have a knight, nor a king'.

This proof is quite long, a little confusing, and hasn't been reviewed properly yet, so it might have mistakes.

The squares with a 3 can't have a knight, because it would then attack 4 squares, of which one is a square with a 2. Above has been proven that square has to be empty. Therefore a knight would attack only 3 non-empty squares, which isn't enough.

To figure out if a king may go in the square, assume it does and extrapolate that decision until either a complete board is created that satisfies the conditions, or a contradiction is detected.

The king on a7 attacks only 4 squares, so they must all have some piece. The piece on b7 can't be a king, because it's not allowed to place 2 kings next to each other like that (see Two Kings Near the Edge). We now have the following board:

Two of the pawns must become kings. If the kings go on a6, and b6, we get two kings next to each other, which isn't allowed. If the kings go on b8 and b6, we get the formation King 15, which isn't allowed (see earlier in this wiki). Therefore the kings have to go on the squares b8 and a6. The knight has to go on b6.

It's now required to place a king on either a5 or b5.

Case 1: The king goes on b5

The knight on b7 attacks only 4 squares, so c9, d8, d6, and c5 must all have some piece. The piece on c9 can't be a knight, because it would attack only 3 squares. Therefore it has to be a king.

The king on c9 attacks only 4 non-empty squares, so c8 and d9 also need to have some piece. Using similar logic as from before, it can get shown the piece on c8 has to be a knight, the piece on d9 has to be a king, and the piece on d8 has to be a knight.

The knight on b6 attacks 5 non-empty squares, of which two are a4 and c4. Therefore at least 1 of those squares must have some piece. The king on b5 already attacks 3 pieces, so the squares a4, b4, c4, and c6 may have at most 1 piece. Combining these facts, and we can conclude that the squares d7 and d5 must have some piece. Furthermore, the squares b4 and c6 must be empty.

The knight on d8 attacks exactly 4 non-empty squares, so the squares e6, f7, and f9 must have some piece. The king on b8 already attacks 4 pieces, so c7 must be empty.

The king on d9 already attacks 1 king and 2 knights, so either e9 or e8 must be a king. e8 isn't allowed to have a king, because it would then attack 5 pieces. Therefore the king must go on e9, and e8 must be empty.

The piece on d7 isn't allowed to be a knight, because it would then attack 3 kings. Therefore it must be a king. Then the pieces on d6, and e6 must also be kings.

A contradiction has been reached. The knight on c8 now attacks 3 kings. Therefore 'Case 1: The king goes on b5' must be false.

Case 2: the king goes on a5

The king on a5 needs to attack one more king and one more knight. There are two ways to place those:

Case 1: the knight goes on a4 and the king on b4

The knight on a4 attacks 4 squares, so c5, c3, and b2 must have some piece. The king on b4 now attacks 4 pieces, so c4, b3, and a3 must be empty.

The knight on b6 attacks 4 non-empty squares, so c8, d7, and d5 must have some piece.

Let's now look at the piece on c8. It can be either a king or a knight.

Case 1, sub-case 1: c8 is a king The king on b8 now attacks 2 kings and 1 knight. The remaining knight can't go on c9, because it would then attack only 3 non-empty squares. Therefore c9 must be empty, and c7 must have a knight.

The king on c8 now attacks 4 pieces, so the squares d9 and d8 must be empty. However, the knight on b7 would then only attack 3 non-empty squares. Therefore case 1, sub-case 1 isn't allowed.

Case 1, sub-case 2: c8 is a knight The knight on b6 now attacks 2 knights and 2 unknown pieces, therefore the pieces on d5 and d7 must be kings.

The king on b8 needs to attack 1 more king. The king can't go on c7, because it would then attack 3 knights. Therefore the king must go on c9, and c7 must be empty.

The king on c9 needs to attack 1 more king and 1 more knight. The knight can't go on d9, because it would then attack only 3 non-empty squares. Therefore the knight must go on d8 and the king on d9.

The knight on c7 attacks 2 kings, 1 knight and 1 unknown piece, so the piece on c5 must be a knight, and d6 must be empty. The new knight on c5 already attacks 2 kings and 2 knights, so the squares e6, e4, and d3 must be empty as well.

c6 isn't allowed to have a knight, because it would attack 4 kings. It's also not allowed to have a knight, because it would attack 4 kings. Therefore c6 must be empty. However, after that the king on d5 would attack only 3 non-empty squares. That's a contradiction, which means 'Case 1: the knight goes on a4 and the king on b4' must be invalid.

Case 2: the knight goes on b4 and the king on a4

The king on a4 needs to attack 1 more king and 1 more knight. The knight isn't allowed to go on a3, so it has to go on b3 and the king must go on a3.

Let's look at square c5. It could either have a king, a knight, or be empty.

Case 1: c5 is a king In this case, the knight on b7 attacks 2 kings and needs to attack 2 more knight. No knight may go on c9, because it would attack only 3 non-empty squares. No knight may go on d6, because then the king on c5 would attack 3 knights. Therefore c5 isn't allowed to be a king.

Case 2: c5 is a knight The knight on c5 already attacks 2 kings and 2 knights, so the squares d7, e6, e4, and d3 must be empty.

The knight on b6 now attacks only 4 non-empty squares, so the squares c8, d5, and c4 must have some piece. c4 isn't allowed to be a king, because it would attack 3 knights, so it must be a knight.

The square c6 can't have a king, because it would attack 3 knights. It also can't have a knight, because it would attack 3 kings. Therefore c6 must be empty. The knight on b4 now attacks only 4 non-empty squares, so the squares a2 and c2 must have some piece.

The king on a3 already attacks 2 knights, so the piece on a2 must be a king, and b2 must be empty. The knight on b4 now attacks 2 kings, and 2 unknown pieces, so the pieces on c3 and d5 must be knights.

The knight on b6 already attacks 2 knights, so the unknown piece on c8 must be a king. The king on b8 now attacks 2 kings and needs to attack 1 more knight. It can't go on c9, so it must go on c7 and c9 must be empty. However, the knight on d5 now attacks 3 knights. Therefore c5 wasn't allowed to get a knight.

Case 3: c5 is empty

The knight on b7 attacks only 4 non-empty squares, so c9, d8, and d6 must have some piece. c9 isn't allowed to be a knight, so it must be a king. The knight on b7 now attacks 2 kings and 2 unknown pieces, so d8 and d6 must be knights.

c8 isn't allowed to have a king, because of the 'no two kings next to each other like that near the edge' rule already mentioned a few times before. So d9 must be the king and c8 must be the knight.

The square c6 isn't allowed to have a king, because it would attack 3 knights. It's also not allowed to have a knight, because it would attack 3 kings. Therefore c6 must be empty.

The knight on d8 now attacks only 4 non-empty squares, so e6, f7, and f9 must have some piece. The knight on d6 already attacks 2 knights, so the piece on f7 must be a king.

The king on b8 already attacks 4 pieces, so c7 must be empty.

Square e8 isn't allowed to have a knight, because then the knight on d6 would attack 3 knights. If e8 has a king, the squares e9 and e7 must be empty. Then the knight on c8 would only attack 3 non-empty squares. Therefore e8 must be empty.

e9 then has to be a king to make sure the king on d9 attacks 2 kings.

d7 isn't allowed to be a knight, because it would attack 3 kings. It's also not allowed to be a king, because it would attack 3 knights. Therefore d7 has to be empty.

The knight on b6 now attacks only 4 non-empty squares, so d5 and c4 must have some piece.

The knight on d6 now attacks 2 knights, 1 king, and 1 unknown piece. So c4 must be a king, e4 must be empty, and f5 must be empty.

The king on c4 already attacks 2 knights, so the piece on d5 must be a king. However, the knight on b4 would then attack 3 kings. This is a contradiction.

All possible cases have been explored, and every path leads to a contradiction. Therefore, square 3 has to be empty.

From Theo Elliott:

Advancing from that list of facts know about the theoretical finite board: 3. Approaching each corner must be a piece who is the last (or possibly only in the case of a knight) piece on that edge.

Given 3 and Stefan's Edge positions above we have 7 cases for that last piece (King 8 and 16 are effectively specific variants of the knight positions, for last piece purposes, and Kings 1, 4, 12, 13 and 15 have been proven impossible by Stefan already.)

King 7 with the black pawn continued down the left edge. King 7

2 Variants of Knight 1 Knight 1a Knight 1b

2 Variants of Knight 2 Knight 2a Knight 2b

Restricted Knight 3

Restricted Knight 4

If all these can be disproved, no finite board exists.

It is worth noting that I think that a theoretical finite board would likely miss the corners by a fair distance.

From Stefan van der Waal:

A program in Python 3.6 that takes in a board with some pieces, and tries to add as many pieces to it as possible.

Link to the Python code

From Ahmed Amrani:

A program in Prolog that tests if there exists a 5x5 chessboard that would work and that can easily get tweaked to work on larger boards:

Link to the Prolog code

• Bishops and Knights

• Knights and Knights

• Knights and Kings unlimited!

• In the Corner

• Two Kings Near the Edge