Option Greeks - Gamma
This is an advanced topic in Option Theory. Please refer to this Options Glossary if you do not understand any of the terms.
Gamma is one of the Option Greeks, and it measures the rate of change of the Delta of the option with respect to a move in the underlying asset. Specifically, the gamma of an option tells us by how much the delta of an option would increase by when the underlying moves by $1. Since delta is a first derivative, thus gamma is a second derivative of the price of the option.
Gamma is represented by \( \gamma \).
The gamma of an option is the second derivative of the option value with respect to the change in the underlying. It is also equal to the rate of change of the delta.
\[ \gamma = \frac{ \partial ^ 2 V } { \partial S ^ 2 } = \frac{ \partial \Delta_ C } { \partial S } \]
As with other option greeks, the unit of Gamma is often ignored. It has a unit of \( 1 / $ \).
Contents
Gamma of Option
The gamma of an option tells us how much the delta of an option would increase when the underlying increases by $1. It allows us to make predictions about how much the delta will change as the underlying changes. This in turn allows us to predict how much the option value would change as the underlying changes.
When the stock is trading at $115, the put option on the $113 strike with 30 days to expiry is worth $1.34. It has a delta of -0.3357 and a gamma of 0.062.
What is the delta of this option when the stock is trading at $117?
The stock has gone up by \( $117 - $115 = $2 \). Since the gamma is \( 0.062 \), hence our best guess of the delta is that it has changed by \( 2 \times 0.062 = 0.124 \). Thus, the delta of the option would be \( -0.3357 + 0.124 = -0.212 \).
The above example shows how knowing the gamma of an option allows us to calculate the delta change which results from a move in the underlying. In turn, we can use that to find the price change from this move. By considering the Taylor series about the current stock price \(S\), the price (in a small neighbourhood about \(S\)) is
\[ V_s \approx V_S + \Delta ( s - S) + \frac{1}{2} \gamma ( s-S)^2. \]
Implications of Put-Call Parity on Delta
The Put-Call Parity states that \( C - P = S - K e ^ { -rt} \). Recall that differentiating it once gives us
\[ \Delta_C - \Delta_P = 1. \]
Let's differentiate this again with respect to the underlying, an we obtain
\[ \gamma_C - \gamma _ P = 0 \Rightarrow \gamma_C = \gamma_P. \]
As such, when we talk about the gamma of an option, we often do not need to specify whether it's the put or the call. We can consider either scenario, and it often easier to consider call options which have a positive delta.
Graph of Gamma
The best way to understand the graph of gamma, is to take the graph of delta and differentiate it point-wise. We take the delta graph (red), find the tangent at each point (blue line), whose slope gives us the value of gamma (blue circle), which we then connect up to get the gamma curve (yellow).
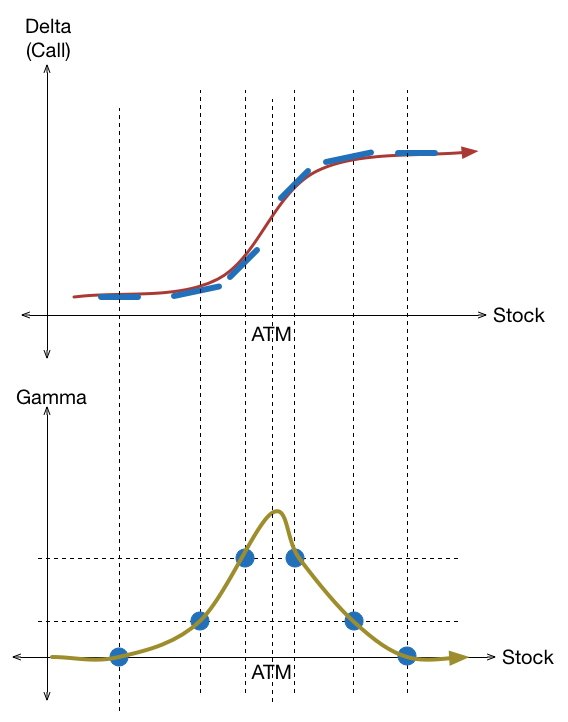
There are several conclusions that we can draw from the above:
- The gamma graph (for constant volatility) looks like a (log-)normal distribution.
- For a given expiry, the gamma of the ATM options is the highest.
Gamma changes over time and volatility
Just as we understood the graph of Gamma from the graph of Delta, we should look at the effect of Delta changes over time and volatility.
As time decreases and volatility decreases, the Delta curve starts to look more like the step function, and thus the Gamma curve starts to look like a normal distribution with lower variance.
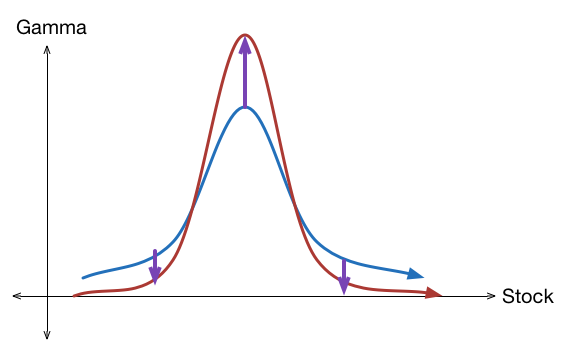
What happens to gamma of an ATM option as volatility increases?
Interpretation of Gamma
Since \( \gamma = \frac{ \partial \Delta_C } { \partial S } \), we can apply the Fundamental Theorem of Calculus to show that
\[ \int_0 ^ \infty \gamma \, dS = [ \Delta_C ]_0 ^ { \infty } = \Delta|_{S = \infty } - \Delta|_{ S = 0 } = 1 - 0 = 1 . \]
A probabilistic interpretation of this result is that delta is the cdf that the strike will be ITM, while gamma is the pdf that the strike is in the money.
The gamma of an option is always positive. We can show this by considering the case of a call option. As the underlying increases, we know that the delta increases, since it is more likely to be ITM. Hence, this tells us that gamma, which is the rate of change of delta, is positive.