Option Greeks - Delta
This is an advanced topic in Option Theory. Please refer to this Options Glossary if you do not understand any of the terms.
Delta is one of the Option Greeks, and it measures the rate of change of the price of the option with respect to a move in the underlying asset. Specifically, the Delta of an option tells us by how much the price of an option would increase by when the underlying moves by $1
Delta is represented by \( \Delta \).
The delta of an option is the rate of change of the price with respect to changes in the price of the underlying.
\[ \Delta = \frac{ \partial V } { \partial S} . \]
Delta is unitless, as it is of the form \( $ / $ \).
Contents
Delta of Option
The delta of an option tells us how much the price of an option would increase when the underlying increases by $1. It allows us to make predictions about how much the option value would change as the underlying changes.
When the stock is trading at $125, the call option on the $140 strike with 80 days to expiry is worth $7.90. If the delta of the option is 0.39, what would be the price of the option when the stock is trading at $127?
The stock has gone up by \( $ 127 - $125 = $2 \). Since the delta of the option is 0.39, our best guess of the option value is that it has increased by \( 2 \times 0.39 = 0.78 \). Thus, the option will be worth \($7.90 + $0.78 = $8.68 \).
The above example shows how knowing the delta of an option allows us to calculate the price change which results from a move in the underlying. This would be accurate as a first-order approximation, and can be further improved if we knew the second order derivative, which is Gamma. When gamma is small, delta can be a sufficient approximation for small moves.
The delta of a call option is positive, which is to be expected, since an increase in the stock price would make the call worth more. A deep In-The-Money call behaves as if one is long the underlying, and hence the corresponding delta is 1. A deep Out-of-The-Money call would have very little change in price as the underlying moves, hence the delta is 0. The range of delta for a call is \( [ 0, 1 ] \).
Similarly, the delta of a put option is negative, since a decrease in the stock price would make the put worth more. A deep ITM delta behaves as if one is short the underlying, and hence the corresponding delta is -1. A deep OTM put would have very little change in price as the underlying moves, hence the delta is 0. The range of delta for a put is \( [-1, 0 ] \).
Often, the delta is expressed as a percentage, instead of a decimal. Thus, people will talk about a delta 50 call instead of a delta 0.5 call. This is easy to differentiate since the delta value is bounded. The main case of confusion could arise when talking about a delta 1 call, in which case it would have to be inferred through context.
An ITM call will approach a delta of 1 as it gets closer to expiry, since the extrinsic value is minimal, and the intrinsic value has a delta of 1. Likewise, an OTM call will approach a delta of 0 as it gets close to expiry, since the intrinsic value has a delta of 0. Conversely, the further out to expiry, the close the delta of a call will get to 0.5. This is because we are less certain if the call will be ITM or OTM. This effect is known as charm.
As the strike increases, the delta of a call decreases. One interpretation of this is that for the same move in the underlying, the price of the upside call is not going to be worth more. Another interpretation is that the upside call is less likely to end up in the money, hence has a lower delta.
Note: Given the limitation of the usefulness of delta to a small move in the underlying, a common usage is to calculate the delta change on a 1 % move. This is given by
\[ \Delta_{1\%} = \Delta \times 1 \% \times S. \]
Implications of Put-Call Parity on Delta
The Put-Call Parity states that \( C - P = S - K e^{-rt } \). Let us differentiate this equation with respect to the stock price S.
On the LHS, we get \( \frac{ \partial } { \partial S } ( C - P ) = \Delta_C - \Delta_P \), which is the delta of the call minus the delta of the put.
On the RHS, we get \( \frac{ \partial}{\partial S} ( S - K e ^ { -rt } ) \). Clearly, the differential of \(S \) with respect to itself is 1. Since \(K \) is a constant, the differential is 0.
Thus, we obtain
\[ \Delta_C - \Delta_ P = 1. \]
This gives us a simple way to calculate the delta of a call when we are given the delta of the put (or vice versa).
Graph of delta
The easiest way to graph the delta of a call, would be to consider what happens to the Option Value as the stock increases.
We get that the graph of delta as the underlying moves is:

We can do the same to graph the delta of the put, or use the relationship that \( \Delta_P = \Delta C - 1 \). Hence,

Note that the delta of the ATM call is just slightly over 0.5. For most purposes, it is close enough to 0.5 that we use that as the approximate value. In actual fact, the delta of the ATM-forward call will be equal to 0.5. Since ATM < ATM-forward, hence the delta will be slightly over 0.5.
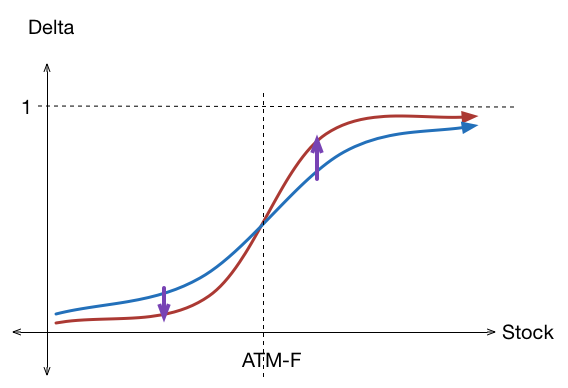
Delta changes over time and volatility
The effect of delta changes over time is more thoroughly explored in Charm.
The effect of delta changes as volatility changes is more thoroughly explored in Vanna.
The following graph is the effect of a decrease in time or volatility on Delta. The blue curve represents an option with more time to expiry (or volatility), and the red curve represents an option on the same strike with less time to expiry (or volatility). As time passes, the Delta curve starts to look more like the step function, and is equal to the step function on expiration.
Interpretations of Delta
The delta of the call has several different interpretations / approximations:
- By definition, \( \Delta = \frac{ \partial V } { \partial S} \).
- Hedge ratio required to remain delta neutral.
- Probability that the Call will end up in the money. This is known as the dual delta, and is a close approximation.
- The negative of the rate of change in the price of the call as the strike increase. \( \Delta \approx - \frac{ \partial V } { \partial X } \).
Which of the following is not a good approximation for delta of a call option?
See Also
* Gamma
* Charm
* Vanna
* Delta correction factor