Option Greeks - Vega
This is an advanced topic in option theory. Please refer to this wiki Options Glossary if you do not understand any of the terms.
Vega is one of the option Greeks, and it measures the rate of change of the price of the option with respect to volatility. Specifically, the vega of an option tells us by how much the price of an option would increase when volatility increases by 1%.
Note that vega isn't an actual greek letter. It is often represented by nu \( (\nu) \), which looks like a "v".
The vega of an option is the sensitivity of the option to a change in volatility:
\[ \nu = \frac{ \partial V } { \partial \sigma }, \]
where
- \( \nu \) is the vega of the option,
- \(V\) is the price of the option, and
- \( \sigma \) is the symbol for volatility.
As with the other Greeks, the units of vega are often ignored/unstated. It has a unit of \( \frac{$}{\sigma}\).
Contents
Vega of Option
The vega of an option tells us how much the price of an option would increase by when volatility increases by 1%. It allows us to make predictions about how much the option value would change as volatility changes.
When the stock is trading at $45, the call option on the $45 strike with 25 days to expiry is worth $3.48 at an implied volatility of 62. If the vega of the option is 0.056, what would be the price of the option when implied volatility is 70?
The volatility has increased by \( 70 - 62 = 8 \) vol points. Since the vega of the option is 0.056, our best guess of the option value is that it has increased by \( 8 \times 0.056 = 0.448 \). Thus, the option will be worth \( $3.48 + $0.448 = $3.93.\ _\square \)
The above example shows how knowing the vega of an option allows us to calculate the price change which results from a volatility change. This would be accurate as a first-order approximation. In the above example, because the vega of an ATM option is mostly constant, the approximation is extremely accurate.
The call option on the 49 strike is currently worth $4.50 and has a vega of 0.11.
How much would the call option be worth if volatility increases by 5%?
The vega of an option is always positive. We know that this is instinctively true, since when volatility goes up, we should be increasing the price of protection/insurance which the options offer.
 As volatility increases, what happens to the price of an option?
As volatility increases, what happens to the price of an option?
Implications of Put-Call Parity on Vega
The put-call parity states that \( C - P = S - K e^{-rt} \). Let us differentiate this equation with respect to volatility:
- On the LHS, we get \( \frac { \partial } { \partial \sigma } ( C - P ) = \nu_C - \nu_P \), which is the vega of the call minus the vega of the put.
- On the RHS, we get \( \frac{ \partial } { \partial \sigma} ( S - K e^{-rt} ) \).
Since the underlying price \(S \) and the present value of the strike \( K e^{-rt} \) are independent of volatility, the RHS is 0. Thus, we obtain
\[ \nu_C - \nu_P = 0 \Longrightarrow \nu_C = \nu_P. \]
This tells us that the vega of the call and the put on the same strike and expiration is the same. Thus, to know the vega of an option on a strike, we can consider either the call or the put option, or even consider the case of the straddle!
For example, let's consider the vega of a straddle. As volatility increases, we are likely to see larger moves in the underlying, which will result in a higher payoff as the underlying moves away from the strike. Thus, the vega of the straddle is positive, which implies that the vega of the individual options is positive. This backs up the observation made in the previous section.
If the vega of the call on the 30 strike is 0.2, what is the vega of the put on the 30 strike of the same expiry?
Graph of Vega
To better understand how vega changes with respect to the underlying, see the wiki Vanna.
Let's consider the graph of vega against the underlying:
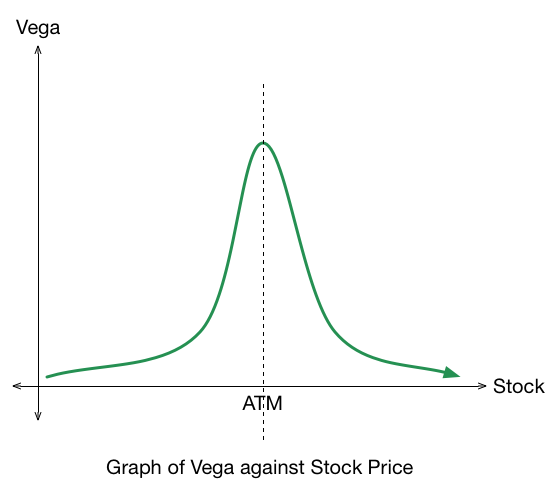
Which of the following options (on the same expiry) has the largest vega when the stock is trading at 100?
Explanation for characteristics of the above graph:
- To think about the vega of an option, we look at the option value. Since the intrinsic value is constant as volatility changes, we should focus on the extrinsic value.
- When the stock is far away from the strike, the extrinsic value is low and an increase in volatility would not affect the payoffs by much. Hence the extrinsic value will not increase significantly, so the vega is low.
- When the stock is near the strike, an increase in volatility has a direct effect on the payoffs. Hence the extrinsic value will increase significantly, so the vega is higher.
Vega Changes over Volatility
Let's consider the graph of vega against volatility:

Explanation for characteristics of the above graph:
- Differentiating the straddle approximation formula with respect to volatility, we see that the ATM vega is pretty constant. (Actually, it is slowly decreasing as volatility increases, but not noticeably so). This is represented by the red line above.
- For the other options, when volatility is 0, the extrinsic value is clearly 0. As volatility increases slightly but not sufficiently enough to affect the payoff which is far away, there would be little change in the extrinsic value, hence a low vega. After a while when the stock is volatile enough to result in a payoff, the extrinsic value would start to increase and thus vega becomes larger.
- Of course, the further away an option is from ATM, the higher the volatility will have to be before this effect takes place. This explains the difference between the green and blue curves.
- For a given volatility, the ATM option has the largest vega, and this sets a maximum limit on the vega of other options.
The stock is trading at 50. For the 55 strike, suppose that we are given the graph of option's vega against volatility. The option has a volatility of 10.
What is the price of the 55 put?
Vega Changes over Time
Let's consider how vega changes over time:
The blue curve represents an option with more time to expiry, and the red curve represents an option on the same strike with less time to expiry.

Explanation for characteristics of the above graph:
- By the straddle approximation formula, the ATM vega is equal to \( \frac{ S \sqrt{t} }{2000} \). Hence, as the time to expiry decreases, the ATM vega decreases.
- A similar effect happens in the wings, since the underlying has less time to move and thus is less likely to affect the extrinsic value.
When the stock is trading at 100, which of the following options have the largest vega?