Partial Derivatives
The partial derivative of a function of multiple variables is the instantaneous rate of change or slope of the function in one of the coordinate directions. Computationally, partial differentiation works the same way as single-variable differentiation with all other variables treated as constant.
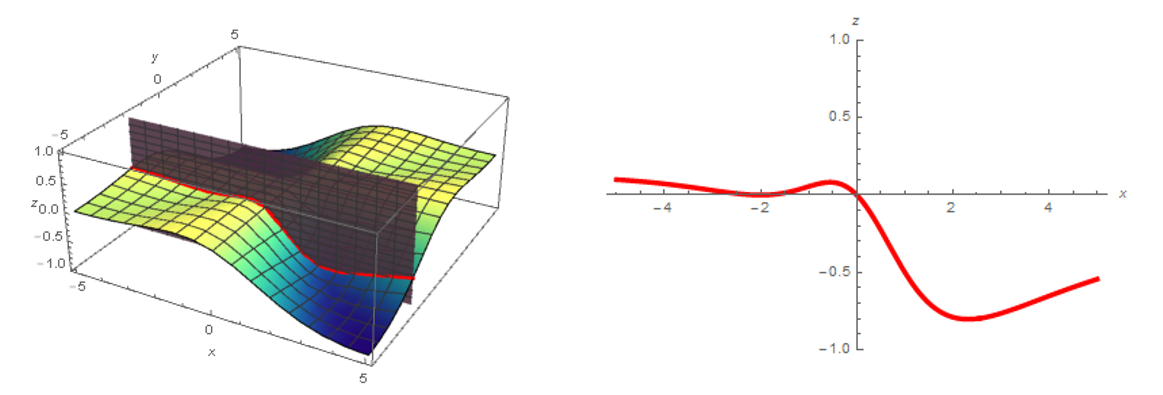 The partial derivative of a function \(f(x,y)\) in the \(x\)-direction can be considered as the usual derivative of the single-variable function \(f(x)\) formed by intersecting \(f\) with the plane of constant \(y\) at any given point. One particular plane of constant \(y\) and the resulting single-variable function (in red) are shown above.
The partial derivative of a function \(f(x,y)\) in the \(x\)-direction can be considered as the usual derivative of the single-variable function \(f(x)\) formed by intersecting \(f\) with the plane of constant \(y\) at any given point. One particular plane of constant \(y\) and the resulting single-variable function (in red) are shown above.
Partial derivatives are ubiquitous throughout equations in fields of higher-level physics and engineering including quantum mechanics, general relativity, thermodynamics and statistical mechanics, electromagnetism, fluid dynamics, and more. Often, they appear in partial differential equations, which are differential equations containing more than one partial derivative.
Contents
Definition
The definition of the partial derivative in the \(x\)-direction of a function \(f\) of two variables \(x\) and \(y\) is
\[\frac{\partial f}{\partial x} = \lim_{h \to 0} \frac{f(x+h,y) - f(x,y)}{h}.\]
Extending this definition to more than two variables is straightforward: all variables besides the variable in the derivative are held fixed in the definition above. The same holds true for partial derivatives in directions other than the \(x\)-direction: for instance, for the partial derivative in the \(y\)-direction the first term in the numerator above is taken to be \(f(x,y+h)\). Note that this definition is the usual difference quotient defining the slope of a tangent line, except with the extra variables held fixed.
Notation for the partial derivative varies significantly depending on context. A frequently used shorthand notation in physics for the left-hand side above includes \(\partial_x f\), while mathematicians will often write \(f_x\) (although this can be ambiguous). In contexts where \(f(x,t)\) is a function of space \(x\) and time \(t\), the dot derivative \(\dot{f}\) will typically denote the partial derivative with respect to time \(\partial_t\) while the prime derivative \(f^{\prime}\) will typically denote the partial derivative with respect to space \(\partial_x\).
All of the usual rules for the ordinary single-variable derivative carry over in the case of partial derivatives:
- Linearity: \(\partial_x (af + bg) = a\partial_x f + b \partial_x g,\) where \(a,b\) are constants and \(f,g\) are functions.
- Product Rule: \(\partial_x (fg) = f\partial_x g + g\partial_x f\).
- Chain Rule: \(\partial_x f\big(g(x)\big) = \frac{\partial f}{\partial g}\frac{\partial g}{\partial x}\).
Since the quotient rule and other rules, such as the power rule, rules for differentiating logarithms and trig functions, etc., can be derived from the above using Taylor series, they are not listed separately, but all such rules still hold.
Compute the partial derivative in the \(y\)-direction of
\[f(x,y) = \sin (xy),\]
first directly from the definition and second by treating the partial derivative as an ordinary derivative with all other variables held constant.
Plugging \(f(x,y) = \sin (xy)\) into the definition gives
\[\frac{\partial f}{\partial y} = \lim_{h \to 0} \frac{f(x,y+h)-f(xy)}{h} = \lim_{h \to 0} \frac{\sin\big(x(y+h)\big) - \sin(xy)}{h} =\frac{\sin(xy + hx) - \sin(xy)}{h} .\]
Now, using the trigonometric identity for the sum, the right-hand side above can be rewritten as
\[\frac{\partial f}{\partial y} =\frac{\sin(xy + hx) - \sin(xy)}{h} = \lim_{h \to 0} \frac{ \sin (xy) \big(\cos (hx) -1\big) + \cos (xy) \sin (hx)}{h}.\]
Evaluating the limits on the right-hand side with L'Hopital's rule, one finds
\[\frac{\partial f}{\partial y} = \lim_{h \to 0} \big(-x \sin(xy) \sin (hx) + x\cos (xy) \cos(hx)\big) = x \cos (xy).\]
Computing the partial derivative instead by treating the \(x\)-variable as a constant, the chain rule gives
\[\frac{\partial f}{\partial y} = \frac{\partial}{\partial y} \big(\sin (xy)\big) = x\cos (xy)\]
in agreement with the first approach. This example demonstrates that the second approach (treating all variables not involved in the derivative as constant) is typically more expedient than computing the partial derivative directly from the definition. \(_\square\)
The original function \(f(x,y) = \sin (xy)\) and its partial derivative \(\partial_y f\) are graphed below for illustration:
Left: the graph of \(f(x,y) = \sin (xy)\). Right: the graph of the partial derivative \(\partial_y f = x\cos (xy)\).
What is the partial derivative in the \(x\)-direction of the function \(f(x,y) = x^2 y^2\) evaluated at the point \((1,1)?\)
The partial derivative everywhere is given by
\[\partial_x f = \partial_x \big(x^2 y^2\big) = 2xy^2.\]
Evaluating at \((x,y) = (1,1)\) gives
\[\partial_x f \bigr|_{(1,1)} = 2(1)(1)^2 = 2.\ _\square\]
Vector Calculus and Higher-order Derivatives
Since there is one partial derivative operator for each coordinate, the partial derivatives of a function can be arranged as a vector, called the gradient and denoted \(\vec{\nabla} f\):
\[\vec{\nabla} f = \left \langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right \rangle.\]
The definition above is written for the three-dimensional case, but the generalization to arbitrary dimensions (including only two dimensions) is straightforward; each component of the vector is a partial derivative in an independent coordinate direction. The operator \(\vec{\nabla}\) is often called the gradient operator or the del operator. It can be treated as a vector of derivative operators:
\[\vec{\nabla} = \left \langle \frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z} \right \rangle.\]
By using the del operator in vector operations like the cross product and dot product, new types of derivative-like objects called the curl \(\vec{\nabla} \times \vec{F}\) and divergence \(\vec{\nabla} \cdot \vec{F}\) can be defined on vector fields \(\vec{F} = \big\langle F_1 (x,y,z) , F_2(x,y,z), \ldots \big\rangle\) in multivariable calculus.
Find the divergence of the vector field \(\vec{F} = \left \langle \frac{x}{x^2+y^2}, \frac{y}{x^2+y^2}\right \rangle \) everywhere outside the origin.
Treating the del operator as a vector, the divergence is given by the dot product
\[ \begin{align} \vec{\nabla} \cdot \vec{F} &= \left \langle \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right \rangle \cdot \left \langle \frac{x}{x^2+y^2}, \frac{y}{x^2+y^2}\right \rangle \\ &= \frac{\partial}{\partial x} \left(\frac{x}{x^2+y^2}\right) + \frac{\partial}{\partial y} \left( \frac{y}{x^2+y^2}\right)\\ &= \frac{2}{x^2+y^2} + \frac{-x(2x)}{\big(x^2+y^2\big)^2} + \frac{-y(2y)}{\big(x^2+y^2\big)^2} \\ &= 0.\ _\square \end{align}\]
Computing higher-order partial derivatives also works the same way as in single-variable calculus; simply apply the derivative operator multiple times:
\[\frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x}\frac{\partial f}{\partial x} = \partial^2_{xx} f = f_{xx},\]
where the rightmost expression is another way of writing the second partial derivative with respect to \(x\). If the two derivative operators are not the same, the higher-order partial derivative is called a mixed partial derivative:
\[\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial}{\partial x}\frac{\partial f}{\partial y} = \partial^2_{xy} f = f_{xy}.\]
Typically (but not always!) the partial derivatives in different directions commute:
\[\partial^2_{xy} f = \partial^2_{yx} f.\]
This is true as long as both of the mixed partial derivatives are continuous.
Show that the mixed partial derivatives of the function
\[f(x,y) = \begin{cases} \dfrac{xy(x^2-y^2)}{x^2+y^2} \quad &(x,y) \neq (0,0) \\\\ 0\quad &(x,y) = (0,0) \end{cases}\]
at the origin are not equal, i.e. the partial derivatives in the \(x\)- and \(y\)-directions do not commute [1].
Consider the restrictions of the partial derivatives of \(f\) to the \(x\)- and \(y\)-axes. Restricted to the \(x\)-axis \((y=0)\) outside the origin, \(\partial_y f\) looks like
\[\partial_y f = \frac{x^5-4 x^3 y^2-x y^4}{(x^2+y^2)^2}\Biggr|_{y=0} = x, \]
and restricted to the \(y\)-axis \((x=0)\) outside the origin, \(\partial_x f\) similarly looks like
\[\partial_x f =\frac{x^4 y+4 x^2 y^3-y^5}{(x^2+y^2)^2} = -y.\]
At the origin, \(\partial^2_{xy} f\) corresponds to \(\partial_x\) of \(\partial_y f\), i.e. a derivative of \(\partial_y f\) taken along the \(x\)-axis. Similarly, \(\partial^2_{yx} f\) corresponds to \(\partial_y\) of \(\partial_x f\), i.e. a derivative of \(\partial_x f\) taken along the \(y\)-axis. Since only the restrictions of the first derivatives to the coordinate axes matter for computation of the second derivatives at the origin, the expressions above suffice. The mixed partial derivatives are therefore
\[\partial^2_{xy} = 1 \neq \partial^2_{yx} = -1,\]
so the partial derivatives in the \(x\)- and \(y\)-directions do not commute.
This follows as a consequence of the failure of the mixed partial derivatives to be continuous can be seen from the graph of \(\partial^2_{xy} f:\)
The different values of the mixed second partial derivatives correspond to the different limits of the expression for the mixed second partial derivative when approaching the origin from different directions.
Just as the first-order partial derivatives could be arranged to form a vector (the gradient), the second-order partial derivatives can be arranged as a matrix called the Hessian matrix:
\[H(f) = \begin{pmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\ \frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2} \end{pmatrix}.\]
The determinant of the Hessian is important in characterizing the stability of critical points where one of the first-order partial derivatives vanish, similar to the use of the second derivative test in single-variable calculus.
Total Derivatives and Fixed Quantities
When dealing with functions of multiple variables, one often sees derivatives written with \(d\) instead of \(\partial\). These derivatives are called total derivatives and are distinct from partial derivatives. For instance, consider a function \(f(x,t)\) where \(x(t)\) is itself some time-dependent position. Since \(x\) itself is time-dependent, the time-dependence of \(f\) depends not only on the explicit form of \(f(x,t)\) but also on the path \(x(t)\). This fact is captured by the total derivative
\[\frac{df}{dt} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial t}.\]
The first term gives the implicit dependence of \(f\) on \(t\) through the time-dependence of \(x\) via the chain rule, while the second term represents the explicit dependence of \(f\) on \(t\).
Compute the total derivative with respect to \(t\) of
\[f(x,t) = x^2 + t^2,\]
where \(x\) represents the path parameterized by \(x(t) = \sin(t)\).
The implicit dependence of \(f\) on \(t\) is
\[\frac{\partial f}{\partial x}\frac{\partial x}{\partial t} = 2x \cos t = \sin (2t).\]
The explicit dependence of \(f\) on \(t\) is
\[\frac{\partial f}{\partial t} = 2t.\]
So the total derivative is
\[\frac{df}{dt} = \sin(2t) + 2t.\]
There is an additional \(\sin (2t)\) term from the time-dependence of \(x\) that is not present in just the partial derivative with respect to \(t\). \(_\square\)
Usually, when computing partial derivatives, it is assumed that all coordinate directions but one are held fixed. However, in some cases (especially in thermodynamics), the quantity that is held fixed for a partial derivative is some combination of the other coordinate variables (like the entropy of an ideal gas, which is a function of temperature and volume). The notation for a partial derivative of a function \(f\) with respect to the coordinate \(x\) holding the quantity \(y\) fixed is
\[\left( \frac{\partial f}{\partial x} \right)_y \quad \text{or} \quad \frac{\partial f}{\partial x} \biggr|_y .\]
Using this notation, one can write a convenient identity called the triple product identity for partial derivatives:
\[\left(\frac{\partial x}{\partial y}\right)_z \left(\frac{\partial y}{\partial z}\right)_x \left(\frac{\partial z}{\partial x}\right)_y = -1.\]
This identity generalizes to cyclic products of \(n\) partial derivatives, with the right-hand side given by \((-1)^n\).
The heat capacity of an ideal gas is defined as the partial derivative of heat input with respect to temperature change. That is, the heat capacity quantifies how responsive the temperature of an ideal gas is to addition of heat. However, depending on how the system is externally maintained, the heat capacity may take different values. Two standard definitions are the heat capacity at constant volume \(C_V\) and the heat capacity at constant pressure \(C_P\), defined by
\[C_V = \left(\frac{\partial Q}{\partial T}\right)_V, \quad C_P= \left(\frac{\partial Q}{\partial T}\right)_P.\]
An extensive derivation shows that the difference between the two heat capacities is given by
\[C_V - C_P = -\frac{T \left(\frac{\partial V}{\partial T} \right)_P^2}{\left(\frac{\partial V}{\partial P}\right)_T}.\]
For an ideal gas \((PV = nRT),\) compute the difference between heat capacities explicitly in terms of the number of moles of gas \(n\) and the gas constant \(R\).
Computing each of the partial derivatives in the given formula using the ideal gas law,
\[ \begin{align} \left(\frac{\partial V}{\partial T} \right)_P &= \frac{\partial}{\partial T} \left(\frac{nRT}P\right) = \frac{nR}{P} \\ \left(\frac{\partial V}{\partial P} \right)_T &= \frac{\partial}{\partial P} \left(\frac{nrT}P\right) = -\frac{nrT}{P^2}. \end{align} \]
Plugging into the given formula, the difference of heat capacities is
\[C_V - C_P = -\frac{T \left(\frac{\partial V}{\partial T} \right)_P^2}{\left(\frac{\partial V}{\partial P}\right)_T} = -\frac{T\left(\frac{nR}P\right)^2}{-\left(\frac{nRT}{P^2}\right)} = nR .\]
This result provides concrete physical proof that the quantity held fixed in computing a partial derivative matters. \(_\square\)
Partial Differential Equations
Partial derivatives in mathematics and the physical sciences are often seen in partial differential equations, differential equations containing more than one partial derivative. Just as ordinary differential equations typically arise by modeling small changes in a system over a small interval of time or space, partial differential equations commonly arise by modeling small changes in a system over both time and space, especially when the change in time affects the change in space and vice versa. A few particularly important partial differential equations are listed below along with a description of the contexts in which each arises, illustrating that partial derivatives are essential for understanding various phenomena throughout the physical sciences:
Wave Equation: \(\displaystyle \frac{1}{v^2} \partial_t^2 u= \partial_x^2 u\)
The wave equation describes the propagation of oscillations of amplitude \(u(x,t)\) of some object, including light waves, pressure waves (sound), and oscillations of physical objects like ropes. Solutions can generically be written as linear combinations of functions \(f(x+vt)\) and \(f(x-vt)\) describing the propagation of a wave to the left or right in time with velocity \(v\).Schrödinger Equation: \(\displaystyle i\hbar\partial_t \psi = -\frac{\hbar^2}{2m} \partial_x^2 \psi + V \psi\)
The Schrödinger equation governs the evolution of wavefunctions \(\psi (x,t)\) in quantum mechanics describing particles of mass \(m\) moving in a potential \(V(x)\). It says that the "velocity" of the probability distribution for the location of a particle is proportional to the curvature of the wavefunction. Localizing a particle in space gives the wavefunction enormous curvature in a small region, so the probability distribution will want to move outward rapidly from this region, in a manifestation of the Heisenberg uncertainty principle.Heat Equation: \(\displaystyle \partial_t T = \alpha \partial_x^2 T\)
The heat equation is similar to the Schrödinger equation with \(V\) set equal to zero. It describes the diffusion of temperature. Similar to the Schrödinger case, the rate at which heat expands outward is proportional to the second derivative or "curvature," where large curvature corresponds to a lot of heat being confined in a small region.Navier-Stokes Equations: \(\displaystyle \big(\partial_t + u_j \partial_{x_j} - \nu \partial^2_{x_j x_j}\big) u_i = - \partial_{x_i} w + g_i\)
The Navier-Stokes equations are extremely important in fluid dynamics, for they constrain the velocity \(u_j\) of a flowing liquid in the \(j^\text{th}\) coordinate direction, \(x_j\). The constant \(\nu\) defines the viscosity, \(w\) defines the work supplied to the system, and \(g_i\) represents applied accelerations to the system in the \(i^\text{th}\) coordinate direction (e.g. from gravity).Einstein Field Equations: \(\displaystyle R_{\mu \nu} - \frac12 R g_{\mu \nu} = \frac{8 \pi G}{c^4} T_{\mu \nu}\)
The Einstein field equations are a set of many coupled partial differential equations that solve for the geometry of spacetime in general relativity in terms of the matter/energy \(T_{\mu \nu}\) that is present in spacetime. The left-hand side above includes the expressions \(R_{\mu \nu}\) and \(R\), which are defined via a complicated combination of partial derivatives of the metric of spacetime \(g_{\mu \nu}\) that governs how distances are measured.Black-Scholes Equation: \(\displaystyle \partial_t V + \frac12 \sigma^2 S^2 \partial_S^2 V + rS \partial_S V - rV = 0\)
The Black-Scholes equation is a well-known application of partial differential equations in finance. It models the price \(V\) of a derivative investment in terms of variables that describe the value of the option: the standard deviation \(\sigma\) of the stock's returns, the price \(S\) of the stock, and the risk-free interest rate \(r\).
References
[1] Weisstein, Eric W. Partial Derivative. From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PartialDerivative.html.