Poynting Vector

The Poynting vector represents the direction of propagation of an electromagnetic wave as well as the energy flux density, or intensity.

Since an electromagnetic wave is composed of an electric field $\big(\vec{E}\big)$ and magnetic field $\big(\vec{B}\big)$ oscillating perpendicular to one another and mutually perpendicular to the direction of the propagation of the wave, the Poynting vector is defined in terms of the cross product of the two fields. The constant in front serves to provide the correct magnitude for the intensity:

$$\vec{S}=\frac{1}{\mu_0}\vec{E}\times\vec{B}.$$

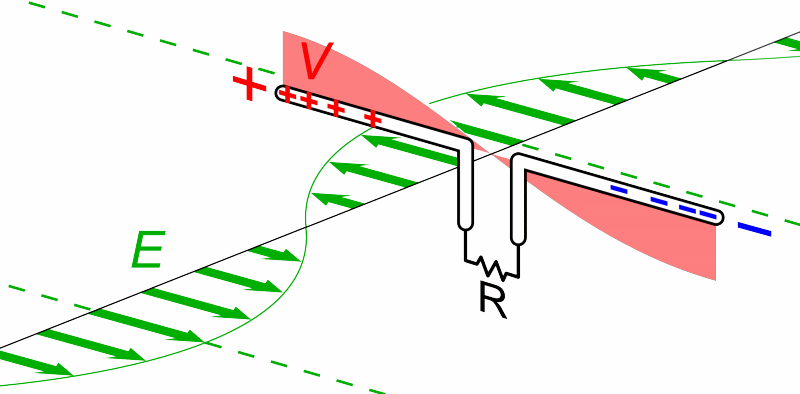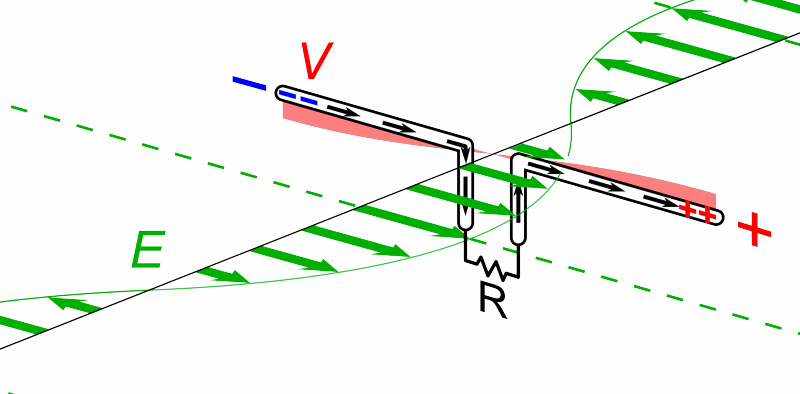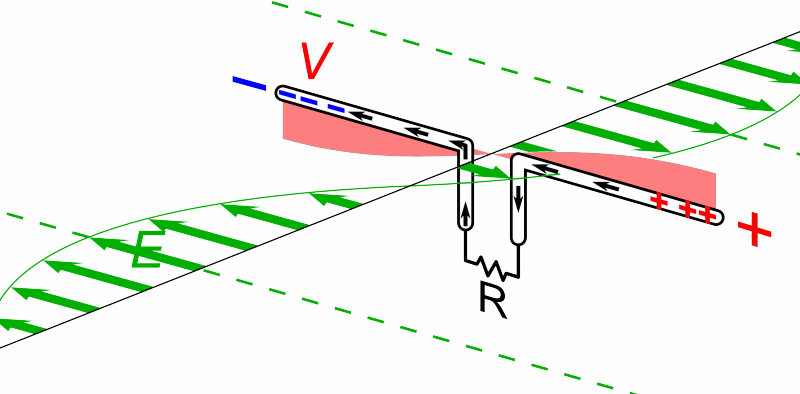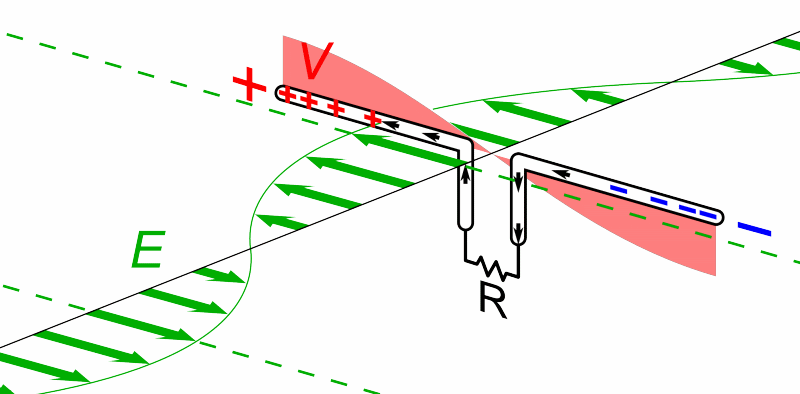This antenna is aligned with the electric field component of an electromagnetic wave in order to capture a signal.

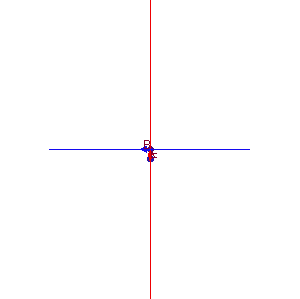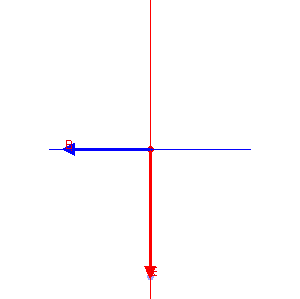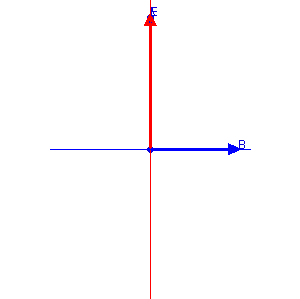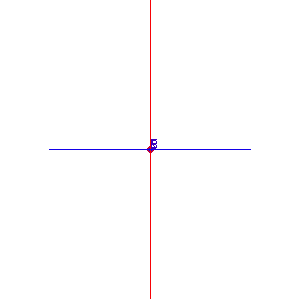The cross product of these oscillating E and B fields at any time indicates the wave is traveling into the page.

If a wave equation is given for an EM wave, the direction of the Poynting vector can be read off. Recall that the general equation for the perpendicular displacement of a point on a string along which a transverse wave is traveling in the $+x$ direction is

$$y(x,t) = y_m\sin(kx-\omega t).$$

Variations within the argument of the sine function account for different directions of propagation.

What is the direction of propagation of the wave described by $$y(x,t) = y_m\sin(kx+\omega t)?$$

---

Changing the $-$ sign in the argument of the sine function to a $+$ sign indicates the direction of propagation is flipped. So, this wave travels in the $-x$ direction. $_\square$

What is the direction of propagation of the wave described by $$x(y,t) = y_m\sin(ky-\omega t)?$$

---

Changing the independent distance variable from $x$ to $y$ indicates the wave travels not in the $x$ direction but in the $y$ direction. $_\square$

By definition, the direction of the Poynting vector must be mutually perpendicular to both the electric and magnetic fields. This relationship is expressed in terms of the cross product of the two fields:

$$\vec{S}=\frac{1}{\mu_0}\vec{E}\times\vec{B}.$$

In practice, this equation is generally only used to find the direction of one of the three, so it helps to remember just the relationship between the unit vectors and the right-hand rule:

$$\hat{S} = \hat{E}\times \hat{B}$$

What is the direction of the Poynting vector for an electromagnetic wave with its electric field component oscillating in the $+y$ direction at an instant when its magnetic field component oscillates in the $-z$ direction?

---

We have

$$\hat{S} = \hat{E}\times \hat{B} = \hat{y} \times -\hat{z} = -( \hat{y} \times \hat{z}) = -(\hat{x}) = -\hat{x}.$$

Hence, the Poynting vector points in the $-x$ direction. $_\square$

The magnitude of the Poynting vector is also called the intensity of the wave. The intensity can be found with the definition of the Poynting vector and the fact that the magnitude of the cross product is $AB\sin\theta.$

$$\vec{S}=\frac{1}{\mu_0}\vec{E}\times\vec{B}$$

Since the electric and magnetic fields oscillate between positive and negative maxima, it is necessary to describe the average value in terms of the root-mean-squares of the field:

$$S = \frac{1}{\mu_0} E_{\text{rms}}B_{\text{rms}}.$$

It is common practice to combine this equation along with the definition of RMS $\big(\text{RMS} = \frac{\text{max}}{\sqrt{2}}\big)$ and $c = \frac EB.$ The intensity is conventionally expressed in terms of just one of the two fields.

$$I = S = \frac{1}{c\mu_0} \frac{E_m^2}{2}$$

A dish with $10\text{ m}$ diameter dish receives a radio signal with a magnetic field amplitude of $7 \text{ pT}.$ Find the power received by the dish.

---

In order to express intensity in terms of magnetic field, incorporate $c = \frac{E}{B}:$

$$I = \frac{1}{c\mu_0} \frac{E_m^2}{2} = \frac{1}{c\mu_0} \frac{(cB)^2}{2} = \frac{cB^2}{2\mu_0}.$$

The power intake of a receptor is $P = IA,$ where $I$ is the intensity and $A$ is the area of the receptor:

$$P = IA = \frac{cB^2A}{2\mu_0} = \frac{c\big(7\times10^{-12}\big)^2\big(\pi(5)^2\big)}{2\mu_0} = 4.59\times10^{-7}\text{ W}.\ _\square$$

Why does the Poynting vector represent intensity? The fundamental equations of electromagnetism are Maxwell's equations: $$\begin{array}{rclcrcl} \nabla \cdot \vec{E} & = & \varepsilon_0^{-1}\rho, & \hspace{.5cm} & \nabla \cdot \vec{B} & = & 0, \\[1ex] \nabla \wedge \vec{E} & = & \displaystyle -\frac{\partial \vec{B}}{\partial t}, & & \nabla \wedge \vec{B} & = & \displaystyle \mu_0\vec{\jmath} + \varepsilon_0\mu_0\frac{\partial \vec{E}}{\partial t}, \end{array}$$ where $\rho$ is the charge density and $\vec{\jmath}$ is the current density of the field. If $V$ is a volume of space bounded by a surface $\partial V$, then $$\begin{aligned} \frac{d}{dt}\int_V \tfrac12\varepsilon_0\big|\vec{E}\big|^2\,d\tau & = \int_V \varepsilon_0 \vec{E} \cdot \frac{\partial \vec{E}}{\partial t}\,d\tau \\ & = \mu_0^{-1}\int_V \vec{E} \cdot\big(\nabla \wedge \vec{B} - \mu_0\vec{\jmath}\big)\,d\tau \\ & = \mu_0^{-1}\int_V \vec{E} \cdot \big(\nabla \wedge \vec{B}\big)\,d\tau - \int_V \vec{E} \cdot \vec{\jmath}\,d\tau \\ \frac{d}{dt}\int_V \tfrac12\mu_0^{-1}\big|\vec{B}\big|^2\,d\tau & = \mu_0^{-1}\int_V \vec{B} \cdot \frac{\partial \vec{B}}{\partial t}\,d\tau \\ & = - \mu_0^{-1}\int_V \vec{B} \cdot (\nabla \wedge \vec{E})\,d\tau. \end{aligned}$$ Thus $$\begin{aligned} \frac{d}{dt}\int_V\left(\tfrac12\varepsilon_0\big|\vec{E}\big|^2 + \tfrac12\mu_0^{-1}\big|\vec{B}\big|^2\right)\,d\tau + \int_V \vec{E} \cdot \vec{\jmath}\,d\tau & = \mu_0^{-1}\int_V\Big[\vec{E} \cdot (\nabla \wedge \vec{B}) - \vec{B} \cdot (\nabla \wedge \vec{E})\Big]\,d\tau \\ & = \mu_0^{-1}\int_V \nabla \cdot \big(\vec{B} \wedge \vec{E}\big)\,d\tau \\ & = \mu_0^{-1} \oint_{\partial V} \big(\vec{B} \wedge \vec{E}\big)\cdot d\vec{\sigma} \end{aligned}$$ so that $$\frac{d}{dt}\int_V\left(\tfrac12\varepsilon_0\big|\vec{E}\big|^2 + \tfrac12\mu_0^{-1}\big|\vec{B}\big|^2\right)\,d\tau + \int_V \vec{E} \cdot \vec{\jmath}\,d\tau + \oint_{\partial V} \vec{S} \cdot d\vec{\sigma} = 0.$$ The first term is the rate of change of the total electromagnetic energy in the field in the volume $V$, while the second term is the rate of work being done by the field due to the movement of charge inside $V$. Conservation of energy considerations tell us that the third term, involving the Poynting vector, must be the rate of flow of energy across the boundary $\partial V$ of the volume $V$, and hence the Poynting vector $\vec{S}$ indeed describes the direction and intensity of the electromagnetic field.