Pricing Forward and Futures
This is an introductory page in Options. If you are unfamiliar with any of the terms, you can refer to the Options Glossary.
Forward and Future contracts can be valued via the present value of all cash flows. We can set up an arbitrage to determine the true value of the future. The bid-ask spread of these contracts would then depend on the liquidity / bid-ask spreads of the underlying.
We will deal with the case of futures, where contracts have been standardized and there is no counter-party risk. The case of forwards is similar, after we account for the differences.
Contents
Forward contract with no intermediate payments
Let now be time \( t=0 \), and the future will expire at time \( t = T \).
Consider the following portfolio:
\[ \begin{array} { l l l }
\text{Transaction} & \text{Now} & \text{Expiry} \\
\text{Buy Spot} & - S_0 & S_T \\
\text{ Borrow money at rate } r & S_0 & - e ^ { r T} S_0 \\
\text{Sell futures contract} & 0 & F_0 - S_T \\
\hline
\text{Net proceeds} & 0 & F_0 - e ^ { rT} S_0\\
\end{array} \]
This is a portfolio which is designed to payout \( F_0 - e ^ { rT} S_0 \) on expiry, with no further costs. If this value was positive, then people would want to buy this portfolio by buying the spot and selling the future. If this value was negative, then people would want to sell this portfolio by selling the spot and buying the future. This activity will cause the portfolio to trade at a value of 0, or that \( F_ 0 - e ^ { rT} S_0 = 0 \). Hence, the current future price can be determined as
\[ F_0 = e^{rT} S_ 0 \]
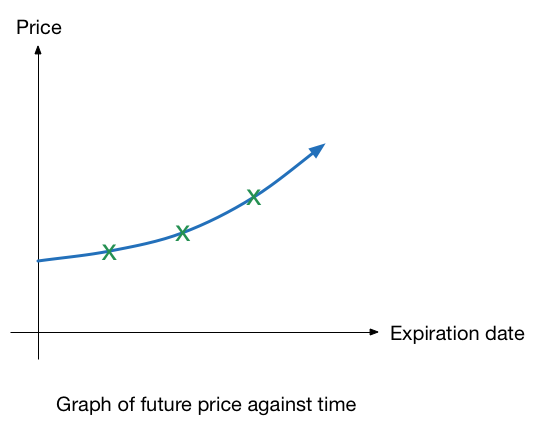
In reality, we can only observe the future price for given expiries, as indicated by the green points. We can interpolate the graph to obtain the overall exponential shape.
Forward contract with intermediate payments
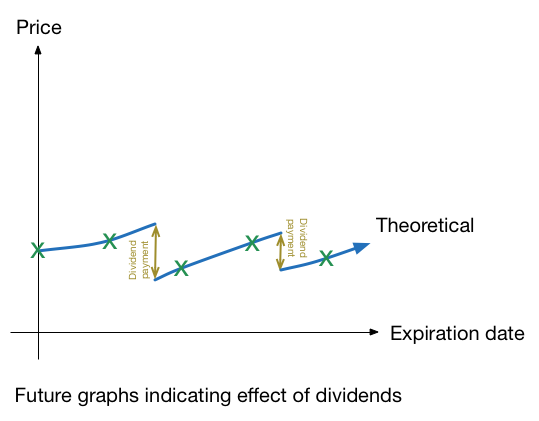
For futures which also consist of dividend payoffs, storage and inventory costs, insurance costs, etc, these also have to be taken into consideration in a similar manner. Let's consider a future which pays a divided at time \( t = t_1 \).
Consider the following portfolio:
\[ \begin{array} { l l l }
\text{Transaction} & \text{Now} & t_1 & \text{Expiry} \\
\text{Buy Spot} & - S_0 & 0 & S_T \\
\text{ Borrow money at rate } r & S_0 & 0 & - e ^ { r T} S_0 \\
\text{Sell futures contract} & 0 & 0 & F_0 - S_T \\
\text{ Receive Dividend} & 0 & D & 0 \\
\text{Reinvest Dividend at } R & 0 & -D & D e ^{ R(T-t_1) } \\
\hline
\text{Net proceeds} & 0 & - & F_0 - e^{rT} S_0 + e ^ { R (T - t_1) }D \\
\end{array} \]
This is a portfolio that is designed to payout \( F_0 - e^{rT} S_0 + e ^ { R (T - t_1) }D \) on expiry. As before, this will be arbitraged to a price of 0. Hence, the current future price can be determined as
\[ F_0 = e^{rT} S_0 - e ^ { R (T - t_1) }D \]
In a similar manner, we can factor in other associated costs.
You calculate that the spot value of the SPY Index is currently $2050. The SPY Futures contract that expires in 6 months is trading at $2050. What would you want to do?
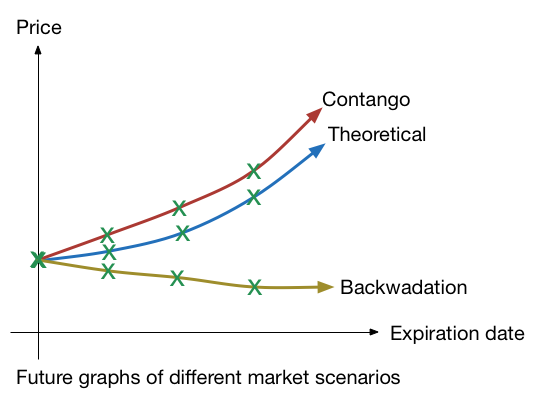
Theoretical prices vs Actual prices
The prices calculated above are the theoretical value of these contracts. Sometime, due to imbalances in supply or demand, the actual prices can be out of line with what we would expect. Over time, they should balance out as arbitragers get paid to take on the risks of executing the portfolio trades as described above. These scenarios are common for commodities which experience a cyclical demand, but supply has to be mostly constant.
A contango refers to the situation when the actual futures price is higher than the theoretically calculated futures price. This can result from
1. Excess supply in the current period which leads to a lower spot price
2. Market mis-pricing of the intermediary costs
3. Demand for the underlying at a later point in time
The price can be corrected by buying the underlying now, holding on to it (and paying the associated costs), and then selling it in future.
A backwardation refers to the situation when the actual futures price is lower than the theoretically calculated futures price. The resulting futures curve is typically downward sloping instead. This can result from
1. Excess demand in the current period which leads to a higher spot price
2. Market mis-pricing of the intermediary costs
3. Perceived supply of the underlying at a later point in time
This scenario is slightly harder to correct for, because selling the underlying now would require delivery / depletion of inventories, so not everyone would be able to execute this trade.
John Mayard Keynes argues that in commodity markets, this arises naturally as producers of commodities are more likely to hedge their price risk than consumers, thus leading to downward pressure in the future months.
If the futures price exceeds the future value of spot plus cost of carry, what would you want to do?
Assume that the future and the spot are both available to trade.