Proofs of the Pythagorean Theorem

Given its long history, there are numerous proofs (more than 350) of the Pythagorean theorem, perhaps more than any other theorem of mathematics.

The proofs below are by no means exhaustive, and have been grouped primarily by the approaches used in the proofs.

Pythagoras's Proof

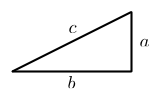
Given any right triangle with legs $a$ and $b$ and hypotenuse $c$ like the above, use four of them to make a square with sides $a+b$ as shown below:

This forms a square in the center with side length $c$ and thus an area of $c^2.$

However, if we rearrange the four triangles as follows, we can see two squares inside the larger square, one that is $a^2$ in area and one that is $b^2$ in area:

Since the larger square has the same area in both cases, i.e. $(a+b)^2$, and since the four triangles are also the same in both cases, we must conclude that the two squares $a^2$ and $b^2$ are in fact equal in area to the larger square $c^2$.

Thus, $a^2 + b^2 = c^2$. $_\square$

Euclid's Proof

In outline, here is how the proof in Euclid's Elements proceeds. The large square is divided into a left and a right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be congruent, proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the areas of the other two squares. The details follow.

Let $A, B, C$ be the vertices of a right triangle with the right angle at $A.$ Drop a perpendicular from $A$ to the square's side opposite the triangle's hypotenuse (as shown below). That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs.

For the formal proof, we require four elementary lemmata:

1. If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent (side-angle-side).
2. The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
3. The area of a rectangle is equal to the product of two adjacent sides.
4. The area of a square is equal to the product of two of its sides (follows from 3).

Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.

Let $ACB$ be a right-angled triangle with right angle $CAB$.

On each of the sides $BC$, $AB$, and $CA$, squares are drawn: $CBDE$, $BAGF$, and $ACIH$, in that order. The construction of squares requires the immediately preceding theorems in Euclid and depends upon the parallel postulate.

From $A$, draw a line parallel to $BD$ and $CE$. It will perpendicularly intersect $BC$ and $DE$ at $K$ and $L$, respectively.

Join $CF$ and $AD$, to form the triangles $BCF$ and $BDA$.

Angles $CAB$ and $BAG$ are both right angles; therefore $C$, $A$, and $G$ are collinear. Similarly for $B$, $A$, and $H$.

Angles $CBD$and $FBA$ are both right angles; therefore angle $ABD$ equals angle $FBC$, since both are the sum of a right angle and angle $ABC$.

Since $AB$ is equal to $FB$ and $BD$ is equal to $BC$, triangle $ABD$ must be congruent to triangle $FBC$.

Since $A$-$K$-$L$ is a straight line parallel to $BD$, rectangle $BDLK$ has twice the area of triangle $ABD$ because they share the base $BD$ and have the same altitude $BK$, i.e. a line normal to their common base, connecting the parallel lines $BD$ and $AL$. (Lemma 2 above)

Since $C$ is collinear with $A$ and $G$, square $BAGF$ must be twice in area to triangle $FBC$.

Therefore, rectangle $BDLK$ must have the same area as square $BAGF,$ which is $AB^2.$

Similarly, it can be shown that rectangle $CKLE$ must have the same area as square $ACIH,$ which is $AC^2.$

Adding these two results, $AB^2 + AC^2 = BD \times BK + KL \times KC.$

Since $BD = KL$, $BD × BK + KL × KC = BD(BK + KC) = BD × BC.$

Therefore, $AB^2 + AC^2 = BC^2$ since $CBDE$ is a square. $_\square$

Using Similar Triangles

Let $ABC$ represent a right triangle, with the right angle located at $C$, as shown in the figure. Draw the altitude from point $C$, and call $D$ its intersection with side $AB$. Point $D$ divides the length of the hypotenuse $c$ into parts $d$ and $e$. The new triangle $ACD$ is similar to triangle $ABC$, because they both have a right angle (by definition of the altitude), and they share the angle at $A$, meaning that the third angle $($which we will call $\theta)$ will be the same in both triangles as well. By a similar reasoning, the triangle $CBD$ is also similar to triangle $ABC$. The proof of similarity of the triangles requires the triangle postulate: the sum of the angles in a triangle is two right angles, and is equivalent to the parallel postulate. The similarity of the triangles leads to the equality of ratios of corresponding sides:

$$\dfrac {BC}{AB} = \dfrac {BD}{BC} ~~ \text{ and } ~~ \dfrac {AC}{AB} = \dfrac {AD}{AC}.$$

The fractions in the first equality are the cosines of the angle $\theta$, whereas those in the second equality are their sines. These ratios can be written as

$$BC^2 = AB \times BD ~~ \text{ and } ~~ AC^2 = AB \times AD.$$

Summing these two equalities results in

$$AC^2 + BC^2 = AB(BD + AD) = AB^2.$$

Therefore,

$$AC^2 + BC^2 = AB^2. \ _\square$$

Two Algebraic Proofs using 4 Sets of Triangles

The theorem can be proved algebraically using four copies of a right triangle with sides $a$, $b,$ and $c$ arranged inside a square with side $c,$ as in the top half of the diagram. The triangles are similar with area ${\frac {1}{2}ab}$, while the small square has side $b - a$ and area $(b - a)^2$. The area of the large square is therefore

$$(b-a)^{2}+4{\frac {ab}{2}}=(b-a)^{2}+2ab=a^{2}+b^{2}.$$

But this is a square with side $c$ and area $c^2$, so

$$c^{2}=a^{2}+b^{2}.$$

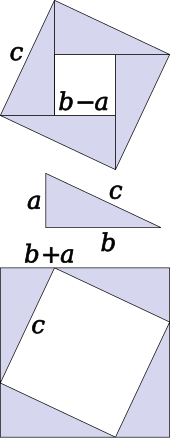
A similar proof uses four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram. This results in a larger square with side $a + b$ and area $(a + b)^2$. The four triangles and the square with side $c$ must have the same area as the larger square:

$$(b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab,$$

giving

$$c^{2}=(b+a)^{2}-2ab=a^{2}+b^{2}.$$

A related proof was published by future U.S. President James A. Garfield. Instead of a square, it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The area of the trapezoid can be calculated to be half the area of the square, that is,

$${\frac {1}{2}}(b+a)^{2}.$$

The inner square is similarly halved and there are only two triangles, so the proof proceeds as above except for a factor of $\frac{1}{2}$, which is removed by multiplying by two to give the result. $_\square$