Propositional Logic
As the name suggests propositional logic is a branch of mathematical logic which studies the logical relationships between propositions (or statements, sentences, assertions) taken as a whole, and connected via logical connectives.
Propositional logic is also known by the names sentential logic, propositional calculus and sentential calculus. It is useful in a variety of fields, including, but not limited to:
- workflow problems
- computer logic gates
- computer science
- game strategies
- designing electrical systems
Contents
Fundamental Concepts - Definitions
In propositional logic a statement (or proposition) is represented by a symbol (or letter) whose relationship with other statements is defined via a set of symbols (or connectives). The statement is described by its truth value which is either true or false.
\(\color{Red} \textbf{Propositions}\)
A proposition is a statement, taken in its entirety, that is either true or false. For example, a proposition might be:
All elephants are green.
Unlike syllogistic logic, in propositional logic, this statement is taken in its entirety, usually represented by a symbol, and we only concern ourselves with whether or not it is true or false, not the individual terms in the statement.
\(\color{Red} \textbf{Proposition Letters}\)
In propositional logic, a proposition by convention is represented by a capital letter, typically boldface. For example, the proposition above might be represented by the letter A.
A: All elephants are green.
\(\color{Red} \textbf{Truth Value}\)
Each of the propositions is assigned a truth value of either true or false. In other areas (for example computer logic gates) these values are given by the binary representations \(1\) (true) and \(0\) (false).
We say that \(v(P)\) evaluates the proposition \(P\), i.e. returns its truth value.
\(\color{Red} \textbf{Connectives}\)
In propositional logic, the relationships between propositions are represented by connectives.
There are essentially five different connectives outlined in the following table:
| \(\color{Blue} \textbf{Connective}\) | \(\color{Blue} \textbf{Symbol}\) | \(\color{Blue} \textbf{Description}\) |
| Negation | \(\neg\) | NOT |
| Conjugation | \(\wedge\) | AND |
| Disjunction | \(\vee\) | OR |
| Conditional | \(\to\) | If ... then |
| Biconditional | \(\leftrightarrow\) | If and only if |
Suppose we wanted to say "If it rains, Jake won't walk to school"
We would first represent the two propositions as a proposition letter:
- A: It rains
- B: Jake won't walk to school
Then we would use the conditional connective to make our statement.
A \(\to\) B \(_\square\)
Truth Table Overview
In order to clarify the meaning of a proposition or a connective, a truth table is used.
Truth tables are a way of visualizing the truth values of propositions. A value of true is represented by a "1" and a value of false is represented by a "0".
For example, consider the following propositions:
- A: Marty wears green boots.
- B: Marty has a dog.
- C: Marty wears green boots, and Marty has a dog.
Proposition C takes on the following truth values:
- If Marty doesn't wear green boots and doesn't have a dog, then proposition C is false.
- If Marty doesn't wear green boots but has a dog, then proposition C is false.
- If Marty wears green boots but doesn't have a dog, then proposition C is false.
- If Marty wears green boots and has a dog, then proposition C is true.
Represented in a truth table, we have one row for each of the above statements (which include all possible combinations of Marty wearing green boots and/or having a dog), and each column represents the possible states of each of the propositions A, B, and, C above.
So, the four statements above are represented in the following truth table:
| \(A\) | \(B\) | \(C = A \wedge B\) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Connectives
Connectives are logical symbols which express the relationship between propositions.
There are five basic connectives:
- Negation
- Conjunction
- Disjunction
- Conditional
- Biconditional
These concepts are further described below.
\(\color{Red} \textbf{Negation}\)
Negation is a unary logical connective. For any proposition \(P\), the negation of \(P\), denoted \(\neg P,\) is a proposition implying that \(P\) is false. \(\neg P\) is also read as "not" \(P\).
\[ v(\neg B) = \left\{\begin{matrix} 1 &&& \text{if } v(B)= 0\\ 0 &&& \text{otherwise.} \ _\square \end{matrix}\right.\]
The truth table (1=true, 0=false) for negation is as follows:
| P | \(\neg\) P |
| 1 | 0 |
| 0 | 1 |
For the proposition:
A: The moon is made of green cheese.
What is \(\neg A\)?
The negation of proposition A, would be a statement which is always true if A is false and always false if A is true. The following statement fits that criteria::
\(\neg\) A: The moon is not made of green cheese. \(_\square\)
\(\color{Red} \textbf{Conjugation}\)
Logical conjunction is an associative binary logical connective which evaluates as true only if both of the propositions it relates are true.
\[ v(A \wedge B) = \left\{\begin{matrix} 1 && \text{if } v(B)= 1 \text{ and } v(A)= 1 \\ 0 && \text{otherwise}. \end{matrix}\right.\]
The truth table for conjugation is as follows:
| P | Q | P \(\wedge\) Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
(1 = true, 0 = false)
Consider the following statement:
The elephants are green, and George wears red boots.
What type of proposition is this?
We can assign propositional letters to these statements:
E: Elephants are green
G: George wears red boots.
Then, the above statement is rewritten as:
E \(\wedge\) G
So, this proposition is a conjunction. \(_\square\)
\(\color{Red} \textbf{Disjunction}\)
Logical disjunction is an associative binary logical connective which evaluates as true if either of the propositions it relates are true. Note: This is the "inclusive" definition of disjunction, not to be confused with the "exclusive" form equivalent to an "XOR" gate in computer logic.
\[ v(A \vee B) = \left\{\begin{matrix} 0 &&& \text{if } v(B)= 0 \text{ and } v(A)= 0 \\ 1 &&& \text{otherwise.} \ _\square \end{matrix}\right.\]
The truth table for disjunction iis as follows:
| P | Q | P \(\vee\) Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
(1 = true, 0 = false)
Consider the following statement:
The elephants are green, or George wears red boots (or both).
Rewrite this using propositional logic.
We can assign propositional letters to these statements:
E: Elephants are green
G: George wears red boots.
Then, the above statement is rewritten as:
E \(\vee\) G \(_\square\)
\(\color{Red} \textbf{Conditional}\)
The logical conditional is the equivalent of the expression "If A then B". The result is true if it is consistent with that statement. The only inconsistent situation is if B is false when A is true. This contradicts the conditional statement. So the definition is as follows:
\[ v(P \to Q) = \left\{\begin{matrix} 0 &&& \text{if } v(P)= 1, v(Q)= 0 \\ 1 &&& \text{otherwise.} \ _\square \end{matrix}\right.\]
And this is the corresponding truth table:
| P | Q | P \(\to\) Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
(1 = true, 0 = false)
Suppose we have the following statement (compound proposition):
If Rebecca finishes her homework, then she can watch Netflix.
Is this a logical conditional?
This consists of the two simple propositions that we will call P and Q:
- P: Rebecca finishes her homework.
- Q: Rebecca watches Netflix.
Then, we can set up the following conditional statement, using a conditional connective:
P \(\to\) Q
So, yes, this is a logical conditional. \(_\square\)
 This is a famous problem in the study of deductive reasoning and logic.
This is a famous problem in the study of deductive reasoning and logic.
You are shown a set of four cards placed on a table, each of which has a number on one side and a colored patch on the other side.
The visible faces of the cards show 3, 8, red and brown.
Which card(s) must you turn over in order to test the truth of the proposition that if a card shows an even number on one face, then its opposite face is red?
\(\color{Red} \textbf{Biconditional}\)
A biconditional is a connective that represents the condition "if and only if".
It checks for whether both of the propositions evaluate to the same truth value. It can also be thought of as \( (A \to B)\wedge(B \to A).\)
\[ v(A \leftrightarrow B) = \left\{\begin{matrix} 1 &&& \text{if } v(A)= v(B) \\ 0 &&& \text{otherwise.} \ _\square \end{matrix}\right.\]
This is equivalent to the XNOR logic gate.
The truth table looks like this:
| P | Q | P \(\leftrightarrow\) Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
(1 = true, 0 = false)
What type of logic proposition is this?:
We will cancel the parade if and only if it rains.
This is equivalent to saying. "If it rains we will cancel the parade, and if we cancel the parade then it's raining." Note: This doesn't imply causation. That is, it doesn't imply that because we cancelled the parade it is raining. In fact it just means that if it isn't raining, we will definitely hold the parade.
We set up the following propositions:
- P: We will cancel the parade.
- Q: It rains.
Then we write our compound proposition as:
\(P \leftrightarrow Q\)
So, it's a biconditional. \( _\square\)
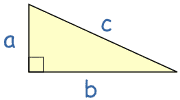
\[\begin{align} A: &\text{ The angle is right.} \\ B: &~a^2 + b^2 = c^2. \end{align} \]
Pythagorean theorem states \(A \to B.\)
The converse says \(B \to A.\)Together, we could claim \(A \leftrightarrow B.\)
In summary, here is a truth table showing the functionality of all of the connectives:
| P | Q | \(\neg\) P | P \(\wedge\) Q | P \(\vee\) Q | P \(\to\) Q | P \(\leftrightarrow\) Q |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Well formed formulae
So far we have discussed the following simple propositions:
- A
- \(\neg\) A
- A \(\wedge\) B
- A \(\vee\) B
- A \(\to\) B
However, we can construct much more complex propositions by combining the above simple propositions to construct an infinite number of combinations of well formed formula, such as:
- \(\neg\) [(A \(\wedge\) B) \(\vee\) C]
A proposition is called a "well formed formula" (or wff) if it is constructed with the following set of rules:
- Any atomic proposition is a well formed formula.
- If \(A\) is a well formed formula, then \(\neg A\) is also a well formed formula.
- If \(A\) and \(B\) are well formed formulae, then \((A \wedge B)\) is also a well formed formula.
- If \(A\) and \(B\) are well formed formulae, then \((A \vee B)\) is also a well formed formula.
- If \(A\) and \(B\) are well formed formulae, then \((A \to B)\) is also a well formed formula.
- If \(A\) and \(B\) are well formed formulae, then \((A \leftrightarrow B)\) is also a well formed formula. \(_\square\)
- Unless constructed using only 1-6 above, then a proposition isn't a well formed formula.
Tautologies, Contradictions and Contingents
\(\color{Red} \textbf{Tautology}\)
A tautology is something that is true just as a matter of logic. An example would be "It is either raining or not raining."
Formally, we say that a proposition is a tautology if it is true for all possible truth assignments of the atomic propositions involved. \(_\square\)
Show that this proposition is a tautology:
\[ ((A \land B) \to C) \leftrightarrow (A \to (B \to C)).\]
We can construct a truth table to verify this:
\(A\) \(B\) \(C\) \(A \land B\) \(((A \land B) \to C)\) \(B \to C\) \((A \to (B \to C))\) 0 0 0 0 1 1 1 0 0 1 0 1 1 1 0 1 0 0 1 0 1 0 1 1 0 1 1 1 1 0 0 0 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0 0 0 1 1 1 1 1 1 1 As you can see, columns 5 and 7 contain identical entries for all combinations of A, B, and C. Therefore, \(((A \land B) \to C) \leftrightarrow (A \to (B \to C))\) is indeed a tautology. \(_\square\)
\(\color{Red} \textbf{Contradiction}\)
A contradiction is a statement that is false just as a matter of logic. An example would be "It is raining and not raining."
Formally, we say that a proposition is a contradiction if it is false for all possible truth assignments of the atomic propositions involved. \(_\square\)
The negation of a tautology is definitely a contradiction.
Since, as demonstrated above, \(((A \land B) \to C) \leftrightarrow (A \to (B \to C))\) is a tautology, the following is a contradiction:
\[\neg (((A \land B) \to C) \leftrightarrow (A \to (B \to C))). \]
\(\color{Red} \textbf{Contingency}\)
A proposition is contingent if and only if it is neither a contradiction nor a tautology. \(_\square\)
An example of a contingency is
\[ (A \land B) \leftrightarrow (A \vee B).\]
We can see this by constructing the truth table:
| \(A\) | \(B\) | \(A \land B\) | \(A \vee B\) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
We can see that since the third and fourth columns neither all match, nor all contradict each other, this is an example of a contingency. i.e. Whether or not proposition is valid is contingent upon the values of \(A\) and \(B\).
Logical Equivalence
Two propositions \(A\) and \(B\) are equivalent if and only if \(A \leftrightarrow B\) is a tautology. \(_\square\)
While the biconditional tests whether the two propositions are of equal value for a particular assignment of truth values, the equivalence is the test for all possible truth value assignments.
Here is a list of several famous logical identities:

In propositional-logic, we have five connectives:
- Negation
- Conjunction
- Disjunction
- Conditional
- Biconditional
Billy argues that this is too many and that any logical proposition that can be constructed with these five connectives can be constructed with fewer.
What is the fewest number of connectives necessary (including only those listed here) in order to be able to construct any logical proposition that can be constructed with these five?
Validity and Consistency
\(\color{Red} \textbf{Validity}\)
So far, we have done nothing to distinguish between a good argument and a terrible one.
There are two ways in which an argument can go wrong:
- The premise is false.
- The logical structure of the argument is wrong.
Since, in propositional logic, we cannot do anything to determine whether the premise is actually true, we define the validity of an argument in terms of the second idea.
\( \left \{ P_1, P_2, \cdots, P_n \right \} \) is said to entail \(C\) if and only if there is no truth assignment for which \( P_1, P_2, \cdots, P_n \) are all true and \(C\) is false. \(_\square\)
We denote entailment as follows:
\[ \left \{ P_1, P_2, \cdots, P_n \right \} \models C. \]
Here is another way to define entailment:
\(\left \{ P_1, P_2, \cdots, P_n \right \} \models C\) if and only if \( ( \left ( P_1 \wedge P_2 \wedge \cdots \wedge P_n \right ) \to C ) \) is a tautology. \(_\square\)
By now, it should be obvious to the reader that an argument is valid if and only if the premise entails the conclusion.
\(\color{Red} \textbf{Consistency}\)
A set of propositions is inconsistent if it cannot be simultaneously all true. Otherwise, it is consistent.
A set of propositions \(\phi = \left \{A_1, A_2, \cdots, A_n \right \}\) is inconsistent if and only if \(\left ( A_1 \wedge A_2 \wedge \cdots \wedge A_n\right )\) is a contradiction.
Otherwise, it is consistent. \(_\square\)
An inconsistent set would be
\[ \phi = \left \{A, A \to B, \neg B, C \right \}. \]
Note that the proposition \(C\) has nothing to do with the inconsistency itself. However, it is a part of an inconsistent set anyway.
Limitations of Propositional Logic
Propositional logic is only one of the many formal languages. It is possible that the structure of an argument is lost in converting it from English to propositional logic.
A natural extension to propositional logic is quantified logic, also called predicate logic or first order logic.
Consider the following famous argument:
- All men are mortal.
- Aristotle is a man.
- Therefore, Aristotle is mortal.
Let us try to symbolize this in propositional logic:
\[\begin{align} A: &\text{ All men are mortal.} \\ B: &\text{ Aristotle is a man.} \\ C: &\text{ Aristotle is mortal.} \end{align}\]
The argument becomes
\[\frac{A, \; B}{\therefore C}. \]
Although clearly a "logical" conslusion, this is a completely invalid argument in propositional logic since A, B and C have no relations to each other.
Note that the problem isn't with the symbolization of the argument. In fact, this is the best symbolization propositional logic can offer for these statements. For this reason, propositional logic is often referred to as "zeroth order logic", whereas quantified logic is referred to as "first order logic" since it looks at the content of the statement to draw a logical conclusion, as in the example above.