RC Circuits (Direct Current)
An RC circuit is created when a resistor and a capacitor are connected to each other. Because a capacitor's voltage is in proportion to electric charge, \(q\) and the resistor's voltage is in proportion to the rate of change of electric charge (current, \(i\)), their interaction within a circuit produces strange results.
Contents
The two cases
There are two cases of RC circuits: Charging RC circuit and Discharging RC circuit.
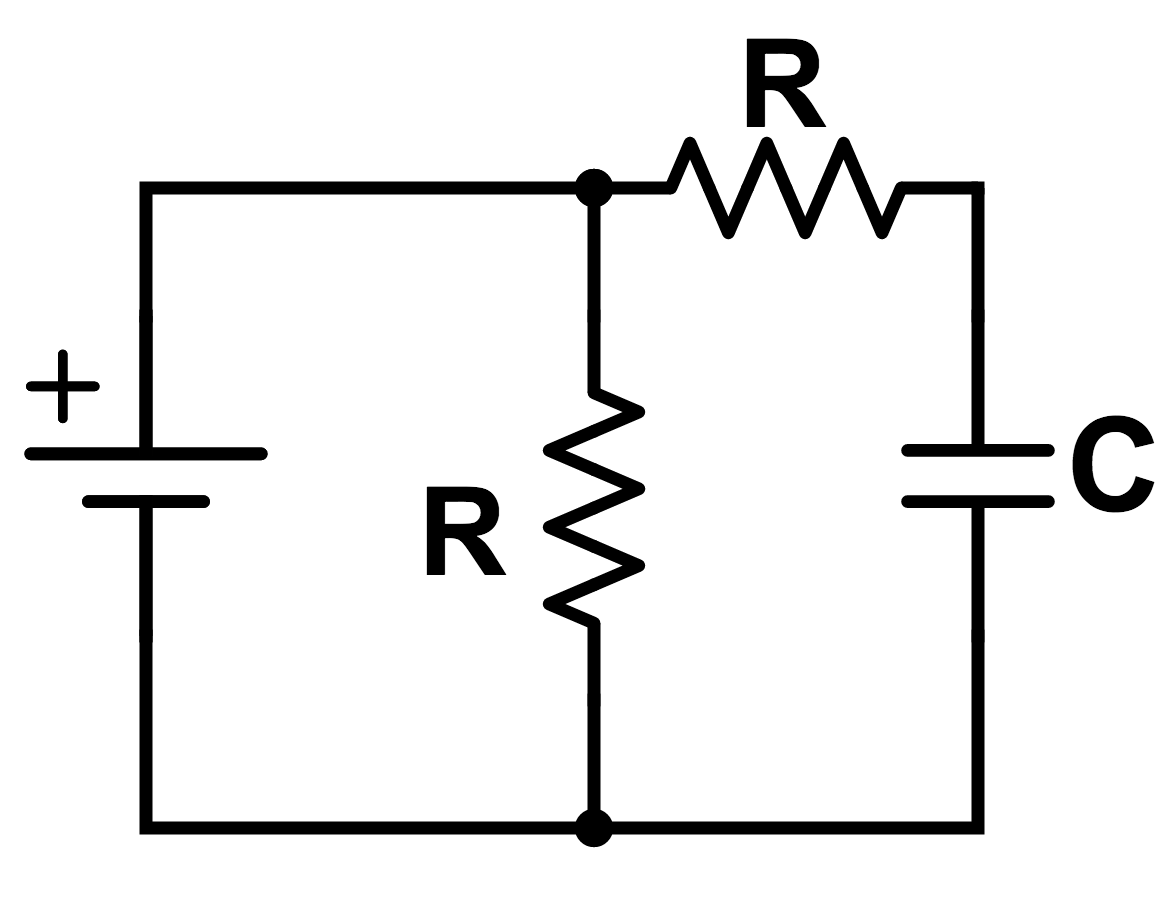
Charging RC Circuit
A charging RC circuit consists of:
A partially charged or completely uncharged capacitor
A resistor
A DC current source
This is the diagram of a basic charging RC circuit.
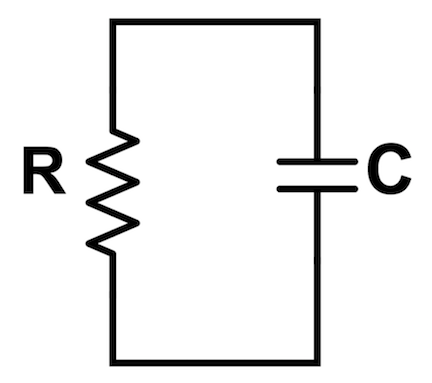
Discharging RC circuit
A discharging RC circuit consists of:
A fully charged or partially charged capacitor
A resistor
Note: in order to discharge, the capacitor must not be connected to a battery.
This is the diagram of a basic discharging RC circuit.
RC circuits physically
Charging case
When a capacitor is connected to a battery, charge is immediately stored on the plates of the capacitor. If a resistor is also connected in series, it will resist the flow of the electrons through the circuit, and delay the charge's building up on the plates of the capacitor. Eventually, the charge will build up on the capacitor, and as no more current flows, the resistor does nothing.
Time = 0 \(\text{s}\)
Since the resistor resists the flow of electrons, the charge stored on the plates of the capacitor is 0 \(\text{C}\) initially.
\[q = 0 \text{ C}\]
\[V_{\text{capacitor}} = \frac{q}{C} = \frac{0}{C} = 0 \text{ V}\]
By Kirchhoff's voltage law the voltage of the battery must be used somewhere. The only other candidate is the resistor.
\[V_{resistor} = \varepsilon\]
\[i = \frac{V_{resistor}}{R} = \frac{\varepsilon}{R}\]
Time approaches infinity
After a long time, the capacitor is allowed to reach its maximum charge. Since no current flows, the resistor uses no voltage.
\[i = 0\ \Omega\]
\[V_{resistor} = iR = 0R = 0 \text{ V}\]
Again, the voltage must be somewhere, and this time the only candidate is the capacitor.
\[V_{capacitor} = \varepsilon\]
\[q = V_{capacitor}C = \varepsilon C\]
When resolving a circuit, treat any capacitors as open switches and resistors as resistance-less wires after a long time.
Discharging case
This time, there is no battery present, so the capacitor and resistor are in parallel. Hence, \(V_{capacitor}=V_{resistor}\) always. The capacitor will release its stored energy through the resistor, which releases the energy in the form of light or heat until there is none left in the circuit.
Time = 0 \(\text{s}\)
The capacitor must be initially charged. Generally this happens by connecting a capacitor to a battery before disconnecting it and connecting it to the resistor.
\[q = q_i\]
\[V_{capacitor} = V_i = \frac{q_i}{C}\]
By Kirchhoff's voltage law the voltage of the resistor is the same as the voltage of the capacitor
\[V_{resistor} = V_{capacitor}\]
\[i = \frac{V_{resistor}}{R}\]
Time approaches infinity
After a long time, the resistor removes all energy from the circuit, so all quantities go to 0.
\[V_{capacitor} = 0 \text{ V}\]
\[q = 0\ \text{C}\]
\[V_{resistor} =0 \text{ V}\]
\[i = 0\ \Omega\]
Find the resistance of the circuit in terms of R at time \(t = 0\ \text{s}.\)
The capacitor uses no voltage initially, so it can be ignored, and the resistors are added in parallel.
\[R_{eq} = (\frac{1}{R_1}+\frac{1}{R_2})^{-1} = (\frac{1}{R}+\frac{1}{R})^{-1} = \frac{R}{2}\]
Find the resistance of the circuit (as seen by the battery) after a very long time.
RC circuits mathematically
Charging case
The goal with a charging RC circuit is to find the charge on the capacitor at any time \(t\).
The charge stored on the capacitor as a function of time is \[q(t) = q_{max} (1 - e^{\frac{-t}{\tau}}).\]
The current through the resistor as a function of time is \[i(t) = \dfrac{q_{max}}{\tau} (e^{\frac{-t}{\tau}}).\]
\(\tau = RC\) is the time constant.
Consider the capacitor of capacitance C to be initially completely uncharged.
At any time \(t\), let the current be \(i\) and the charge on the capacitor be \(q.\)
Applying Kirchoff's Loop Law,
\(\varepsilon - iR - \dfrac{q}{C} = 0.\)
Since \(i = \dfrac{dq}{dt},\) the above equation becomes
\(\varepsilon - \dfrac{dq}{dt} R- \dfrac{q}{C} = 0.\)
This is a first order differential equation in \(q\) and \(t.\)
The solution to this differential equation is
\(q = C\varepsilon (1 - e^{\frac{-t}{RC}}).\)
Since \(V_{capacitor} = \frac{q}{C},\)
\(C\varepsilon \rightarrow \) is the maximum charge on the capacitor, and hence can be denoted as \(q_{max}.\)
\(RC \rightarrow \) is called the time constant of the circuit, and is generally denoted by the Greek Letter \(\tau.\) It is trivially the time it take for the capacitor to reach 63.2% of the maximum charge.
The complete equation for the charge on the capacitor at any time \(t\) is thus
\(q = q_{max} (1 - e^{\frac{-t}{\tau}}).\)
The current in the circuit at time \(t\) is the derivative of the above equation.
\(i = \dfrac{q_{max}}{\tau} (e^{\frac{-t}{\tau}})\)
Here \(\dfrac{q_{max}}{\tau}\) is the maximum current in the circuit, and is denoted by \(i_{max}.\)
Discharging case
The goal with a discharging RC circuit is to find the charge on the capacitor at any time \(t\).
The charge stored on the capacitor as a function of time is \[q(t) = q_{max} e^{\frac{-t}{\tau}}.\]
The current through the resistor as a function of time is \[i(t) = -\dfrac{q_{max}}{\tau} (e^{\frac{-t}{\tau}}).\]
\(\tau = RC\) is the time constant.
Consider the capacitor of capacitance C to be initially completely charged with charge \(q_{max}.\) (This generally comes from previously being connected to a battery.)
At any time \(t\), let the current be \(i\) and the charge on the capacitor be \(q.\)
Applying Kirchoff's Loop Law,
\(- iR - \dfrac{q}{C} = 0.\)
Since \(i = \dfrac{dq}{dt},\) the above equation becomes
\(- \dfrac{dq}{dt} R- \dfrac{q}{C} = 0.\)
This is a differential equation in \(q\) and \(t.\)
The solution for this differential equation is
\(q = q_{max} (e^{\frac{-t}{RC}}).\)
Again, \(RC \rightarrow \) is called the time constant of the circuit, and is generally denoted by the Greek letter \(\tau.\)
Hence the complete equation that gives us the charge on the capacitor at any time \(t\) is
\(q = q_{max} (e^{\frac{-t}{\tau}}).\)
Differentiate to generate the equation for the current.
\(i(t) = -\dfrac{q_{max}}{\tau} (e^{\frac{-t}{\tau}})\)
A 5 \(\text{F}\) capacitor is connected in series to a 4 \(\text{V}\) battery, a 3 \(\Omega\) resistor, and a switch. What is the charge on the capacitor, in \(\text{C}\), when the switch has been closed for \(15 \ln10 \text{ s}\)?
