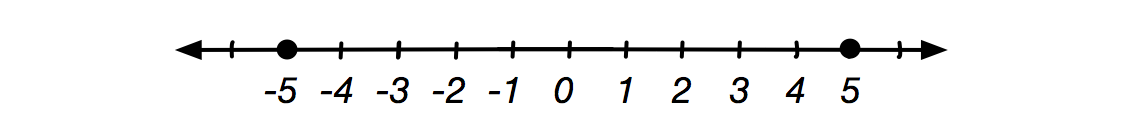Representation on the Real Line
One way to visually represent the real numbers \(\mathbb{R}\) is by a real number line, a horizontal line such that each point on the line corresponds to a real number and each real number corresponds to a point on the line.
Contents
Representing Real Numbers
Since the number line represents all real numbers and since zero is a real number, there is a point on the line that represents zero (called the origin). Then the points on the line to the right of the origin represent positive numbers while the points on the line to the left of the origin represent negative numbers.
In the following visualization of the real number line, the integers are marked as evenly spaced points on the line, but the real number line also represents all real numbers in between the integers and extending to infinity in both directions.
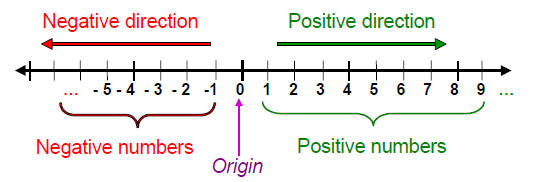 Real
Real
In the problems below, we will assume that the evenly spaced tick marks correspond to integers, and one unit corresponds to the distance between consecutive integers.
On the number line pictured below, what is the real value represented by point \(a\)?

Solution: Since the evenly spaced tick marks correspond to consecutive integers, we can label the tick marks around point \(a\) as follows:

This shows point \(a\) represents the real value \(4\).
Properties
There are many useful properties of the real number line. Consider two real numbers \(a\) and \(b\) represented by points on the real number line such that the point \(a\) lies to the left of the point \(b\) on the line. Then the real numbers \(a\) and \(b\) satisfy
- \(a \leq b\)
- the distance between \(a\) and \(b\) is \( \lvert a - b \lvert = \lvert b - a \lvert \), or the length of the line segment with endpoints \(a\) and \(b\)
In other words, the points on the real number line respects the ordering of the real numbers. The real number line is useful in helping with visualizing addition, subtraction, and intervals of real numbers.
On the number line pictured below, which of the following is a possible value for the point \(a\)?

A) 3.52
B) 1.89
C) 2.73
D) 4.65
Solution: Since the evenly spaced tick marks correspond to consecutive integers, we can label the tick marks around point \(a\) as follows:

This shows that the real number \(a\) lies in between integers \(2\) and \(3\), and the only real number in the answers satisfying this property is 2.73, so the answer is (C)
What is the inequality represented by the red portion of the real number line?

Solution: We first label the tick marks using the reference point corresponding to real number -1:

Then the red portion of the real number line corresponds to all real numbers less than or equal to \(-3\), and the inequality is \(x \leq -3\).
Note that if the point \(a\) is the same as the point \(b\) on the number line, then
- \(a = b\)
- the distance between \(a\) and \(b\) is \( \lvert a - b \lvert = 0\)
What is the length of the red line segment on the real number line?

Solution: We first label the tick marks around the origin:

The the length of the red line segment is \( \lvert 3 - (-2) \rvert = \lvert 3 + 2 \rvert = 5\). This can also be obtained by counting the number of units between the two points.
Mark the points on the real number line with distance \(5\) from the origin.
Solution: The two points on the real number line with distance \(5\) from the origin are \(-5\) and \(5,\) which can be marked as follows: