SAT Circles
To successfully solve problems about circles on the SAT, you need to know:
- how to find the circumference and area of a circle
- the definition of a central angle
- about tangent lines to a circle
- the definition of arc measure, arc length, and sector area
- how to solve simple problems about inscribed and circumscribed figures
Contents
Examples
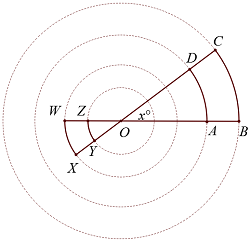
In the figure above, the circles are concentric, points \(X, Y, O, D,\) and \(C\) are collinear, and so are points \(W, Z, O, A,\) and \(B.\) Which of the following has the greatest value?
(A) \(\ \ m \widehat{WX}\)
(B) \(\ \ m \widehat{AD}\)
(C) \( \ \ m \widehat{BC}\)
(D) \(\ \ 2 m \widehat{ZY}\)
(E) \(\) It cannot be determined from the information given.
Correct Answer: D
Solution:
Tip: The measure of an arc equals the measure of its central angle.
\(\angle COB \cong \angle XOW\) because they are vertical angles. Therefore,\[m \angle COB = m \angle DOA = m \angle XOW = m \angle YOZ = x.\]
The measure of an arc is defined as the measure of its central angle. Remember that it is not the same as arc length. It follows that
\[m \widehat{CB} = m \widehat{DA} = m \widehat{XW} = m \widehat{YZ} = x.\]
So, the arcs in choices (A), (B), and (C) have the same measure.
The quantity in answer choice (D), \(2 m \widehat{ZY} = 2x > x,\) and it has the greatest value. Therefore (D) is the correct answer.
Since we were able to find the measures in all of the choices, (E) cannot be true.
Incorrect Choices:
(A), (B), (C), and (E)
The solution explains why these choices are wrong.
What is the circumference of a circle whose radius is \(\pi ?\)
(A) \(\ \ 2\pi\)
(B) \(\ \ \pi^2\)
(C) \(\ \ 2\pi^2\)
(D) \(\ \ \pi^3\)
(E) \(\ \ 4\pi^2\)
Correct Answer: C
Solution:
We use the formula for finding the circumference of a circle.
\(C = 2 \pi r = 2\pi \cdot \pi = 2 \pi^2.\)
Incorrect Choices:
(A)
You will get this wrong answer if you use the wrong formula \(C=2\pi,\) instead of \(C=2\pi r,\) or if you find the diameter of the circle instead of its circumference.(B)
You will get this wrong answer if, to find the circumference of the circle, you use the wrong formula \(C=\pi r\) instead of \(C=2\pi r.\)(D)
If you find the area of a circle with radius \(\pi\) instead of its circumference, you will get this wrong answer.(E)
If you use the wrong formula for finding the circumference of a circle using its diameter, \(C=2 \pi d,\) instead of \(C=\pi d,\) you will get this wrong answer.
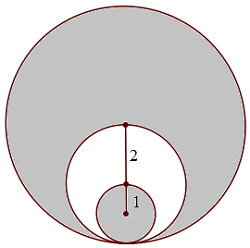 As shown in the figure above, the three circles are tangent, the middle circle passes through the center of the big circle, and the small circle passes through the center of the middle circle. What is the area of the shaded region?
As shown in the figure above, the three circles are tangent, the middle circle passes through the center of the big circle, and the small circle passes through the center of the middle circle. What is the area of the shaded region?
(A) \(\ \ 6\pi\)
(B) \(\ \ 11\pi\)
(C) \(\ \ 13\pi \)
(D) \(\ \ 19 \pi\)
(E) \(\ \ 21\pi\)

In the diagram above, the square circumscribes circle \(\bigodot O.\) If the area of the square is 100, and the length of \(\overline{OB}\) is 3, what is the area of \(\triangle XYO?\)
(A) \(\ \ 6\)
(B) \(\ \ 12\)
(C) \(\ \ 100 - 25\pi\)
(D) \(\ \ 24\)
(E) \(\ \ 25\pi\)
Correct Answer: B
Solution:
Let the side of the square be \(s.\) First, we find \(s.\)
\[\begin{align} A_{\square} = s^2 = 100\\ s = 10\\ \end{align}\]
Let the radius of the circle be \(r.\) Since the square is circumscribed, its side equals the diameter of the circle, or it is twice as long as the radius of the circle. It follows that
\[\begin{align} 2r = s = 10\\ r = 5\\ \end{align}\]
This is shown in the diagram below.

The diagram indicates that \(\triangle XBO\) is a right triangle. By the Pythagorean theorem, \(XB^2 = 5^2-3^2 = 16\) and \(XB = 4.\)
Since \(\triangle XYO\) is an isosceles triangle, its altitude \(\overline{OB}\) is also a median. Therefore, \(XB = BY\) and \(XY = 4+4 = 8.\)
We know the base of \(\triangle XYO,\) we know its height is \(ZB = 3+5 = 8,\) and therefore, its area is \(A_{\triangle XYO} = \frac{1}{2} \cdot 3 \cdot 8 = 12.\)
Incorrect Choices:
(A)
Tip: Read the entire question carefully.
If you find \(A_{\triangle XBO}\) or \(A_{\triangle YBO}\) instead of \(A_{\triangle XYO},\) you will get this wrong answer.(C)
If you think the area of the triangle equals the area of the square minus the area of the circle, you will get this wrong answer.(D)
Tip: Area of a triangle with height \(h\) and base \(b\): \(A_{\triangle} = \frac{1}{2}bh.\)
If you use the wrong formula \(A = bh\) to find the area of the triangle, you will get this wrong answer. The formula for finding the area of a triangle is \(A = \frac{1}{2}bh.\)(E)
This is the area of the circle, not of \(A_{\triangle XYO}.\)
Review
If you thought these examples difficult and you need to review the material, these links will help:
SAT Tips for Circles
- The circumference of a circle with radius \(r\) and diameter \(d: C = 2\pi r = \pi d.\)
- Area of a circle with radius \(r: A_{\bigodot} = \pi r^2.\)
- The measure of an arc equals the measure of its central angle.
- The length of an arc with measure \(x\) is \(\frac{x}{360}\cdot 2 \pi r.\)
- The area of the sector formed by an arc measuring \(x\) and two radii is \(\frac{x}{360} \cdot \pi r^2.\)
- SAT General Tips