Section Formula

The section formula tells us the coordinates of the point which divides a given line segment into two parts such that their lengths are in the ratio \(m:n\).

The midpoint of a line segment is the point that divides a line segment in two equal halves. The section formula builds on it and is a more powerful tool; it locates the point dividing the line segment in any desired ratio.

The section formula is helpful in coordinate geometry; for instance, it can be used to find out the centroid, incenter and excenters of a triangle. It has applications in physics too; it helps find the center of mass of systems, equilibrium points, and more.

If point \(P (x,y)\) lies on line segment \(\overline{AB}\) \((\)between points \(A\) and \(B)\) and satisfies \(AP:PB=m:n,\) then we say that \(P\) divides \(\overline{AB}\) internally in the ratio \(m:n.\) The point of division has the coordinates

\[P=\left( \dfrac{mx_2 + nx_1}{m+n}, \dfrac{my_2 + ny_1}{m+n} \right). \]

The formula can be derived by constructing two similar right triangles, as shown below. Their hypotenuses are along the line segment and are in the ratio \(m:n\).

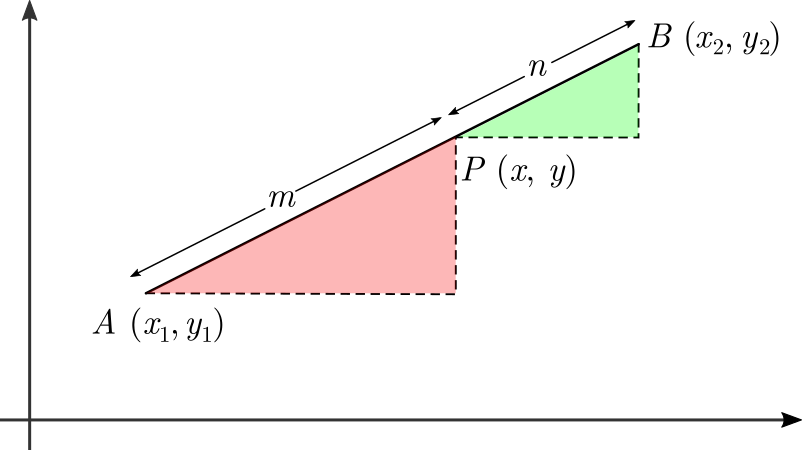
The red and the green triangles are similar since the corresponding angles of the triangles are equal. This implies that the ratio of their corresponding sides are equal. Note that point \(P\) is \(\frac{m}{m+n} \times AB\) away from \(A\). That is,

\[\begin{align} x & = x_1 + \frac{m}{m + n} (x_2 - x_1) \\ & = \frac{(m + n) x_1 + m x_2 - m x _1}{m + n} \\ & = \frac{ m{ x }_{ 2 }+n{ x }_{ 1 }}{m + n}. \qquad (1) \end{align}\]

Similarly, solving for \(y\) gives

\[ y= \frac{m{ y }_{ 2 }+n{ y }_{ 1 }}{m + n}. \qquad (2)\]

Therefore, from \((1)\) and \((2)\)

\[P (x,y) = \left( \dfrac { m{ x }_{ 2 }+n{ x }_{ 1 } }{ m+n }, \dfrac { m{ y }_{ 2 }+n{ y }_{ 1 } }{ m+n } \right).\ _\square\]

As a special case of internal division, if \(P\) is the midpoint of \(\overline{AB}\), then it divides \(\overline{AB}\) internally in the ratio \(1:1\). Hence applying the formula for internal division and substituting \(m = n = 1\), we get

\[P=\left( \dfrac{x_1+y_1}{2}, \dfrac{x_2+y_2}{2} \right). \]

Given \(A=(-3,1)\) and \(B=(3,-6)\), what are the coordinates of point \(P=(x,y)\) which internally divides line segment \(\overline{AB}\) in the ratio \(1:2?\)

ANSWER

The point \(P\) is \(\frac{1}{1+2} \times AB\) away from point \(A\).

When measured parallel to the \(x\)-axis, we get

\[\begin{align} x & = -3 + \frac{1}{3} \times \big(3 - (-3)\big) \\
&= -1. \end{align}\]

When measured parallel to the \(y\)-axis, we get

\[\begin{align} y & = 1 + \frac{1}{3} \times (-6 -1) \\ & = - \frac{4}{3}. \end{align}\]

Thus, the coordinates of \(P\) are \(\big( -1, -\frac{4}{3} \big) \) \(_\square\)

Given \(A=(-3,6)\), what are the coordinates of \(B=(x_2,y_2)\) if point \(P=(-2,4)\) divides line segment \(\overline{AB}\) internally in the ratio \(1:3?\)

ANSWER

In this example, we are to find one of the endpoints of the line segment. Drawing similar triangles will help us solve this problem too.

The sides of the triangle are in the ratio \(1 : 3\). The base of the pink triangle has length \(-2 - (-3) = 1\). The base of the green triangle is three times as long, that is, \(x - (-2) = 3 \times 1\). Solving this yields \(x = 1\).

The height of the pink triangle is \(4 - 6 = -2\). The height of the green triangle is three times as long, that is, \(y - 4 = 3 \times (-2)\). Solving this equation yields \(y = -2\).

Thus, the coordinates of \(B\) are \((1,-2).\) \(_\square\)

Given \(A= (-2,-1)\) and \(B=(4,11)\), point \(P= (x,y)\) internally divides line segment \(\overline{AB}\) in the ratio \(m:n\). If \(P \) is the intersection point of \(\overline{AB}\) and the \(y\)-axis, what is the value of \(m : n?\)

ANSWER

Since point \(P\) is on the \(y\)-axis, its \(x\) coordinate is zero. We can write the coordinates of \(P\) as \((0, y)\).

The horizontal distance between \(P \) and \(A\) is \(0 - (-2) = 2\).
The horizontal distance between \(B\) and \(P\) is \(4 - 0 = 4\).

The ratio of the bases of the right triangles is \(2 : 4\), or \(1 : 2\). Since the triangles are similar, the ratio of their hypotenuses is also \(1 : 2\).

Therefore, point \(P\) divides line segment \(AB\) in the ratio \(1 : 2\). \(_\square\)

In what ratio does the point \(P=(-3,7)\) divide the line segment joining \(A=(-5,11)\) and \(B=(4,-7)?\)

ANSWER

We can draw 2 similar right triangles: the red triangle with hypotenuse \(AP\) and the blue triangle with hypotenuse \(PB.\)

Point \(P\) divides line segment \(AB\) in the ratio \(AP : PB\), which is equivalent to \(a:b\) since the triangles are similar. Let us find the lengths of \(a\) and \(b:\)

\[a = (-3) - (-5) = 2, \quad b = 4 - (-3) = 7.\]

Thus, point \(P\) divides line segment \(AB\) in the ratio \(a : b = 2 : 7\).

Alternatively, the ratio \(AP : PB\) is also equal to \(c : d,\) i.e.

\[c = 7 - 11 = -4, \quad d = (-7) - 7 = -14 \implies c:d=2:7.\]

We get the ratio \(2 : 7\) again, which is consistent with our previous calculations. \(_\square\)

To solve questions similar to the above example there is an alternative method in which you need to solve only for one variable instead of two variables. Below given example demonstrates it.

Find the ratio in which the point \((5,4)\) divides the line joining points \((2,1)\) and \((7,6)\).

ANSWER

You can solve this question in normal method by assuming the ration to be \(m : n\). But now we will take a different substitution. Assume \(k = \dfrac{m}{n}\) so that \(m : n = k : 1\). Now the required ratio will be \(k : 1\). \[P~(x,y) = \left(\dfrac{kx_2 + x_1}{k + 1} \quad , \quad y = \dfrac{ky_2 + y_1}{k + 1}\right)\] Given that the point \(P = (5,4)\). So, substitute either \(x\) or \(y\) in the above result.

\(x = \dfrac{kx_2 + x_1}{k + 1} \implies 5 = \dfrac{7k + 2}{k + 1}\)

\(\implies k = \dfrac{3}{2}\).

Find the co-ordinates of point \(P\) which divides the line joining \(A = (4 , -5)\) and \(B = (6 , 3)\) in the ratio \(2 : 5\).

ANSWER

Let the co-ordinates of \(P\) be \((x , y)\). \[\begin{align} P~(x , y) & = \left(\dfrac{2 \times 6 + 5 \times 4}{2 + 5} , \dfrac{2 \times 3 + 5 \times -5}{2 + 5} \right) \\ P~(x , y) & = \left(\dfrac{12 + 20}{7} , \dfrac{6 - 25}{7} \right) \\ \therefore P & = \left(\dfrac{32}{7} , -\dfrac{19}{7} \right) \\ \end{align}\]

Find the co-ordinates of the mid-point of the line segment joining the points \((4,-6)\) and \((-2,4)\).

ANSWER

\[Mid~Point = \left(\dfrac{x_1 + x_2}{2} , \dfrac{y_1 + y_2}{2} \right) = \left(\dfrac{4 - 2}{2} , \dfrac{-6 + 4}{2} \right) = (1,-1)\]

You can find more about midpoint in this wiki.

If \(P = (x,y)\) lies on the extention of line segment \(\overline{AB}\) \((\)not lying between points \(A\) and \(B)\) and satisfies \(AP:PB=m:n,\) then we say that \(P\) divides \(\overline{AB}\) externally in the ratio \(m:n.\) The point of division is

\[P=\left( \dfrac{mx_2 - nx_1}{m-n}, \dfrac{my_2 - ny_1}{m-n} \right) .\]

This proof of this result is similar to the proof in internal divisions, by drawing two similar right triangles. The yellow and orange triangles have their sides in the ratio \(m : n\).

From the figure, we see that point \(P\) is at a distance of \(\frac{m}{m-n} \times AB\) away from point \(A:\)

\[\begin{align} x & = x_1 + \frac{m}{m - n} (x_2 - x_1) \\ & = \frac{(m - n)x_1 + mx_2 - mx_1 }{m-n} \\ & = \frac{mx_2 - nx_1}{m-n}. \qquad (3) \end{align}\]

Similarly, solving for \(y\) gives

\[y=\frac { m{ y }_{ 2 }-n{ y }_{ 1 } }{ m-n }. \qquad (4)\]

Therefore, from \((3)\) and \((4)\)

\[ P(x, y) = \left( \dfrac { m{ x }_{ 2 }-n{ x }_{ 1 } }{ m-n }, \dfrac { m{ y }_{ 2 }-n{ y }_{ 1 } }{ m-n } \right).\ _\square\]

If points \(P\) and \(Q\) which lie on line segment \(AB\) divide it into three equal parts that means, if AP = PQ = QB then the points \(P\) and \(Q\) are called Points Of Trisection of \(AB\).

The thing you should remember is that \(P\) divides \(AB\) in the ratio \(2 : 1\) and \(Q\) divides \(AB\) in the ratio \(1 : 2\).

• 3D Coordinate Geometry - Equation of a Line

• Linear Equations - Intersection of Lines

• Coordinate Geometry - Angle Bisector