Shunting Yard Algorithm

The way we write mathematical expressions is infix notation. Operators have precedence and brackets override this precedence. Many programs require the parsing calculation on the fly. One very good way to do this is to convert from infix notation to some intermediate format. In this case, we will be using a very common and simple format called reverse polish notation.

The shunting yard algorithm is a simple technique for parsing infix expressions containing binary operators of varying precedence. In general, the algorithm assigns to each operator its correct operands, taking into account the order of precedence. It can, therefore, be used to evaluate the expression immediately, to convert it into postfix, or to construct the corresponding syntax tree.

The shunting yard algorithm is not your basic algorithm like mergesort, string search, etc. It is quite advanced as stacks, queues, and arrays are all contained in the same algorithm. Although the algorithm itself is very simple, a solid flexible implementation might be thousands of lines of code.

Before we have our program calculate expressions, we need to convert them into an intermediate notation where the operators are in the order they must be performed. Unlike humans who look at infix expressions in their head, computers must be told explicitly what the order of the operations and parameters should be. The most common intermediate format is the reverse polish.

The procedure used is as follows:

• Expressions are parsed left to right.
• Each time a number or operand is read, we push it to the stack.
• Each time an operator comes up, we pop the required operands from the stack, perform the operations, and push the result back to the stack.
• We are finished when there are no tokens (numbers, operators, or any other mathematical symbol) to read. The final number on the stack is the result.

Consider the following infix notations:

$$4+18/(9-3).$$

Now we know that the answer to this from the rule or order of operations is $7$.

We have not seen it yet, given the above infix notation, that the shunting yard algorithm will output the reverse polish notation as

$$4, 18, 9, 3, -, /, +.$$

Note that the commas are not part of the reverse polish, but used to separate each token.

Using the procedure for reverse polish,

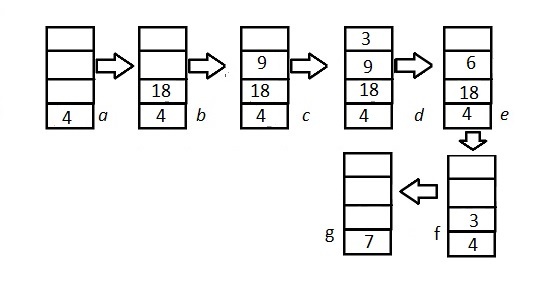
In steps $a$ to $d$, we push the numbers in reverse polish expression into the stack. In step $e$, where we have reached the operator sign $(-)$, we pop the two numbers involved, perform the operation $9-3=6$, and push it back to the stack. Next is the operator sign $(/)$, where we pop the $6$ and $18$ and perform the operation $18/6=3$ and push it to the stack. We continue with the procedure until we are left with a single number that is $7$.

To build the algorithm, we will need

• 1 stack for operations
• 1 queue of the output
• 1 array (or other list) of tokens.

A pseudocode of the algorithm is as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

1.  While there are tokens to be read:
2.        Read a token
3.        If it's a number add it to queue
4.        If it's an operator
5.               While there's an operator on the top of the stack with greater precedence:
6.                       Pop operators from the stack onto the output queue
7.               Push the current operator onto the stack
8.        If it's a left bracket push it onto the stack
9.        If it's a right bracket 
10.            While there's not a left bracket at the top of the stack:
11.                     Pop operators from the stack onto the output queue.
12.             Pop the left bracket from the stack and discard it
13. While there are operators on the stack, pop them to the queue

The algorithm is fairly simple. Consider the infix notation again. To solve it, let us set up an array of list, a stack, and a queue.

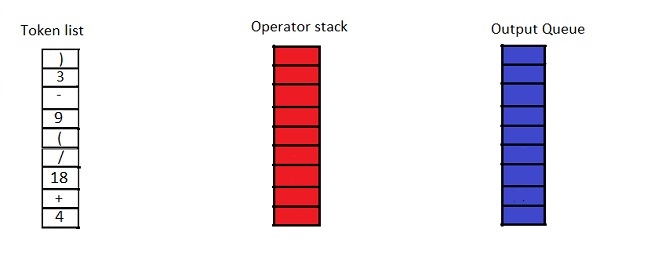
The list of tokens in the left is filled from bottom to top and is the same as the infix expression stated earlier. We are now going to fill the stack and the queue bottom up, according to the shunting yard algorithm.

We read the tokens bottom up, so the number $4$ goes to the output queue. The next element which is an operator sign $(+)$, according to the algorithm in lines $4, 5$ and $6,$ will be pushed onto the stack because an empty stack does not have any element of precedence.

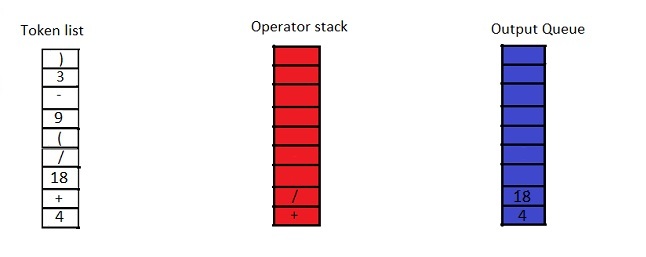
Since the addition operator has less precedence than division, we ignore lines $5$ and $6$. When we get a left bracket, we push it onto the stack, and when we get a right bracket, according to lines $10$ and $11,$ we pop operators from the stack into output queue until the left bracket is reached. Then we discard the left bracket.

Finally, when we are left with operators in the stack, we pop them to the queue.

That is it: the output queue contains the reverse polish notation, which as we have already seen can be computed to give the final answer.