Signals and Systems

The study of signals and systems concerns two things: information and how that information affects things. A strict definition of a signal is a time-varying occurrence that conveys information, and a strict definition of system is a collection of modules which take in signals and generate some sort of response.

It may be easier to think about these terms with a real-world situation. Imagine that you are trying to build a robot that steers straight down a line on the floor. The system here is a robot and a line. Let's assume there is machinery that allows the robot to "sense" the line on the floor, and it uses a camera. The signals here would be the visual data from the camera. But now comes the hard part: how do we take in that signal and use it to tell the robot what to do next? One guess might be as follows: if the robot is on the right of the line, steer left, if it is on the left of the line, steer right, and if it is on the line, steer straight. This seems pretty good, but watch what happens when it is put into action:

A robot that has a simple controller

As you can see, we will overshoot the line every time. It's not so easy to develop an algorithm that perfectly models this system, but that's the goal of this entire field of study. Signals and systems are areas that are used in every single field of technology, electronics, and engineering. As we saw above, all pieces of hardware that need to sense the world around them (robots, wearable technology like fitbits, radar) need to be able to recognize signals and change their systems appropriately. Signals are also used in systems like your computer. Signals between tiny components in your computer allow it to share information and function. It's these basic elements of hardware that allow all software to function.

Signals, as discussed above, convey information. However, it is usually more useful to think about them as functions where the independent variable is time and the dependent variable is some data. So, a signal function might look like this:

\[ f(t) = 2 \cdot t .\]

The graph corresponding to this signal would look like this:

Signal with function \(f(t) = 2 \cdot t\)

A given system can have many possible input signals and output signals. Take the example of the robot from earlier. The robot could be using a camera to sense the color of the line. It could also be using its tires to kinetically sense the line if the line has any distinctive physical properties. It could even be using magnetic forces if the line was coated in certain materials. While the input signal is typically defined by the environment around the system, the system has much more control over the output signal. The output signal can be anything that can be used to tell the robot what to do with its steering.

Try to think of some possible output signals for the robot's system. Remember, the output signal can be anything that can be used to tell the robot what to do next. When you've thought of some, click on the Show Answer button to see some more ideas.

Show Answer

The output signal could be as follows:

• rotational speeds for all of its wheels (they will be different if the car needs to turn)
• desired temperatures for all the wheels (using a mapping from friction-induced temperature to rotational speed)
• a 3D vector describing the next desired position (if the robot is using vectors to describe its own position)
• its desired distance to the line at the next time step.

There are many more, but not all output signals are smart choices. It's up to you, the system designer, to choose an output signal that makes sense.

There are many types of signals, and often signals are just composed of multiple signals. Here are a few basic signals and their associated signal functions.

Unit Step Function

This signal sends out a unit signal of magnitude 1 at time 0. This signal continues indefinitely. The term "unit" is used to denote that the magnitude becomes 1. If the magnitude is not equal to 1, it is just a step function. This signal is also known as the Heaviside function:

\[u(t) = \begin{cases} 1 & \mbox{if } t \geq 0 \\\\ 0 & \mbox{if } t \lt 0. \end{cases}\]

Unit Step Function

You can think about the step function like plugging in something to a wall outlet. Before you plug it in, there is no signal coming through. Once you do, there is a constant signal as long as you have it plugged in.

Unit Impulse Function

This signal only sends out a pulse of unit 1 at time 0. Otherwise, there is no signal:

\[\sigma(t) = \begin{cases} 1 & \mbox{if } t = 0 \\\\ 0 & \mbox{if } t \neq 0.\end{cases}\]

Unit Impulse Function

Ramp Signal

This signal has a linear relationship with time:

\[r(t) = \begin{cases} t & \mbox{if } t \geq 0 \\\\ 0 & \mbox{if } t \lt 0. \end{cases}\]

Ramp Function

The ramp signal can describe the speed of something falling down a ramp. As it falls due to gravity, its velocity will increase linearly. That linear relationship is what is described by the ramp signal.

Parabolic Signal

The parabolic signal has a quadratic relationship to time:

\[x(t) = \begin{cases} \frac{t^{2}}2 & \mbox{if } t \geq 0 \\\\ 0 & \mbox{if } t \lt 0.\end{cases}\]

Parabolic Signal

Sinusoidal Signal

This signal follows the path of a sinusoid \(\big(\)either \(\sin(x)\) or \(\cos(x)\big).\) These signals are very important because they are the basis for Fourier analysis and Fourier series. They are used often in electrical engineering:

\[x(t) = \begin{cases} A \cdot \cos(w_0 \cdot t\pm \phi) \text{ or}\\\\ A \cdot \sin(w_0 \cdot t\pm \phi). \end{cases}\]

The entire world of signals can be grouped into classes, each of which has important properties. Additionally, these classes have opposite classes. For example, the opposite of a continuous signal is a discrete signal. A signal can be defined using multiple classes, as long as two opposing classes are not used.

Continuous and Discrete Signals

Continuous signals are signals for which the value of the signal is defined at every time interval. It's very much like the signals described in the above section.

Discrete signals are signals for which the value of the signal is defined only at discrete instants of time, for example, maybe every second. A discrete time signal's graph looks like this:

Discrete Time Signal (red arrows) and Continuous Time Signal (gray line) ^[1]

There is important math involved in translating between continuous signals and discrete signals. Oftentimes, sampling is used to convert from continuous signals found in the real world to discrete signals used in signal analysis. Changing the domain of your signal, as in the case of converting from continuous to discrete, is often used in signal processing.

Deterministic and Non-deterministic Signals

Deterministic signals are signals where there is no uncertainty of its value at any time. Any signal that can be defined using a mathematical formula, such as the unit step function, is deterministic.

Non-deterministic signals have an element of randomness in their value and thus cannot be defined using any well-defined mathematical formula. These are instead modeled using probabilistic formulas.

Even and Odd Signals

A signal is even if it satisfies the equation \(f(t) = f(-t)\). In other words, even function are symmetric about the \(y\)-axis. A signal is odd if it satisfies the equation \(f(t) = -f(-t)\). In other words, about the \(y\)-axis, the signal is mirrored about the \(x\)-axis. For example, \(\cos(t)\) is an even signal, and \(\sin(t)\) is an odd signal.

A signal can be even or odd; or it can be neither, as most are.

Even Signal ^[2]

Odd Signal ^[2]

Periodic and Aperiodic Signals

A signal is periodic if it satisfies the equation \(f(t) = f(t + T)\), where \(T\) is the fundamental time period. What this is really saying is if the signal \(f(t)\) repeats every \(T\) time, it is periodic. An aperiodic function does not repeat. An example of a period signal is any sinusoidal signal like \(\cos(x)\). An example of an aperiodic signal is the unit impulse signal. It signals a pulse at \(f(0)\) but then nothing afterwards.

Real and Imaginary Signals

A signal is real if, at every point in time, its value is 100% real and the imaginary unit part is zero. Conversely, a signal is imaginary if its value is all imaginary at every point in time.

Signals can be built from other signals. Indeed, most signals can be defined as compositions of smaller, more basic signals. The basic operations boil down to two main types: those that deal with amplitude, and those that deal with time.

Amplitude

Operations on signals that affect amplitude follow the basic mathematical operations: addition and multiplication. The addition of two signals results in a signal that has their summed amplitudes at every time step. So, summing two signals, \(X_0\) and \(X_1\) results in \(X_2\). That means at every possible time step, \(X_2\) has a signal value that is the sum of the values of \(X_0\) and \(X_1\) at that time step.

For example, if we were to sum the unit step function and the ramp function from earlier, the result would look like this:

Addition of unit step signal and ramp signal

Subtraction is the exact same process except for the amplitudes of the two signals are subtracted.

Multiplication and division work the same way except for the amplitudes of the two signals are multiplied or divided at every time step. The same holds true when scaling a single signal with a scalar value. Multiplying a signal by the number 3 will return a signal whose amplitude at every time step is 3 times the amplitude of the input signal at that time step.

Algebraic relationships work the same way. For example,

\[c \cdot \big(X_0(t) + X_1(t)\big) = cX_0(t) + cX_1(t) .\]

Time

It's possible to change a signal's time by shifting it, scaling it, or reversing it. Time shifting takes a signal \(X_0(t)\) and shifts it by a value, \(t_0\). This shift can be positive or negative to indicate which direction in time the signal is being shifted. The result is \(X_0(t \pm t_0)\).

Time-shifting a rectangular signal forward

Time scaling will either compress or expand the signal. For example, if a signal is defined from \(t = -2\) to \(t = 2\), and its time is scaled by a factor of 2, the new signal will be defined from \(t = -4\) to \(t = 4\).

Time reversal is an operation where the signal \(f(t)\) is turned into \(f(-t)\). This new signal is the input signal, mirrored about the \(y\)-axis.

At its most abstract, a system is simply a collection of elements that takes in an input and responds with an output, as in the following graphic:

System Overview

There are many types of systems and ways to control them. They all have important use cases and applications in the field of systems.

There are three ways that systems are generally represented:

• difference equations
• block diagrams
• operator equations.

Difference equations are mathematical ways of expressing systems, and they are often recursive (it depends on earlier states). As an example, let's look at the Fibonacci sequence. At each step of this sequence, we add the two previous inputs. So, if we define \(x[n]\) as the current input and \(y[n]\) as the output at a given time step, then

\[y[n] = y[n-1] + y[n-2] + x[n] \]

describes the Fibonacci sequence. Here, \(x[n]\) is a signal whose value equals 1 at time = 0 and zero thereafter. It is the exact same as the unit impulse signal from above. The difference equation, also sometimes called the recurrence relation, is important because it allows us to mathematically manipulate these elements.

A block diagram is a graphical way of representing systems. It is composed of the elements in a system, connected by directional arrows that dictate the flow of information. There are three important primitive elements, or devices, in these block diagrams:

1. Delay: This rectangular device delays the signal by a time step.
2. Scale: This triangular device will scale the incoming signal by a scalar term, \(c\) (also sometimes called a buffer).
3. Adder: This circular component will add (or subtract) multiple signals.

Again, let's look at the Fibonacci sequence. We know we need some sort of memory, so delays will be necessary. Also, we have to add numbers together, so we'll need an adder as well. In fact, the block diagram will look like this:

Fibonacci Block Diagram

In this diagram, there are two feedback loops. One will delay the signal by one-time step, the other by two-time steps. So, the adder is eventually going to add the outputs from the previous two-time steps to get the current output. That is the Fibonacci sequence.

The operator equation is very similar to the difference equation, but it uses elements from the block diagram. The operator equation is a relationship between the input and output signals using the scaling, adders, and delays of the block diagram. So, the operator equation for our Fibonacci system would look like

\[Y = X + \mathcal{R}X + \mathcal{R}^2X .\]

\(\mathcal{R}\) is used to denote delay on an input signal. These operator equations (also sometimes called system functions) are used often in predicting system behavior.

Systems have classes, just as signals do, and they can be defined in these classes in the same way. However, there are also two important control classes that systems can have. A system can be an open loop, it can a feedback system, and it can be a feedforward system.

An open loop is a simple control flow abstraction that only uses its current state, a model of the system, and the input signal. It is the most basic system controller paradigm. An example of a feedback system is our robot from earlier. The robot takes in the environment, decides how next to move, and continues.

A feedback system takes data from its output to help decide how next to operate. If we wanted to change our robot's system to be a feedback system, we might feedback data that tells the robot how much closer it got to the line. If we got too close, we might want to back off our steering so that we don't overshoot the line by too much.

A feedforward system will actually pass data from the environment forward in its system. A cool example of a feedforward system is actually in your body. As you age, your brain learns that certain activities cause certain levels of stress. So, in anticipation of those activities, your brain can spike things like your adrenaline levels. So, next time you walk up to a treadmill and your heart starts to beat a little faster, you can thank feedforward systems!

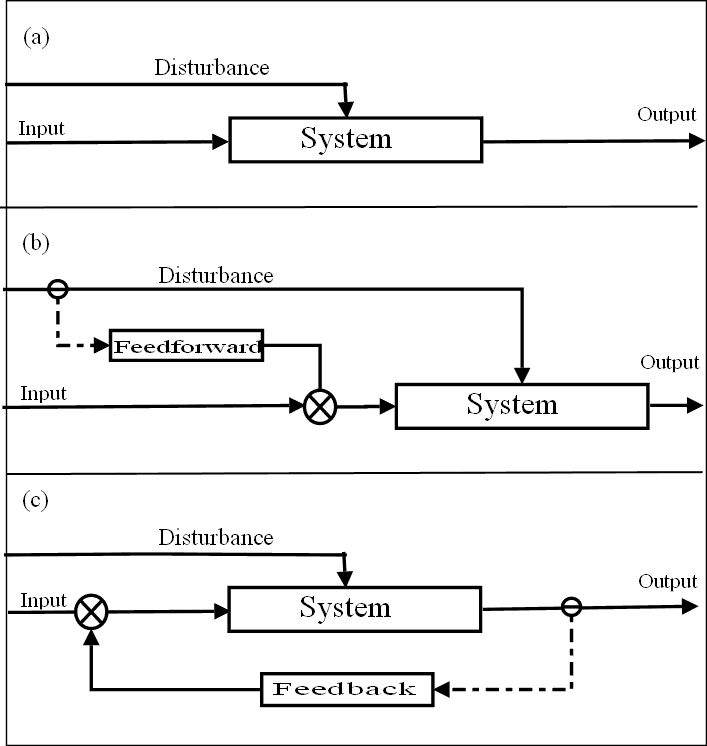Types of System Control: (a) Open Loop (b) Feedforward (c) Feedback ^[3]

There are different types of systems as well. These systems are as follows:

• Linear and Non-linear Systems
  A system is linear if it satisfies the following property, where signals \(x_1(t)\) and \(x_2(t)\) output \(y_1(t)\) and \(y_2(t)\), respectively: \[T\big[a_1x_1(t) + a_2x_2(t)\big] = a_1T\big[x_1(t)\big] + a_2T\big[x_2(t)\big] = a_1y_1(t) + a_2y_2(t) .\] Linear systems are typically much simpler than their non-linear counterparts. They are used in automatic control theory, signal processing, and telecommunications. Specifically, wireless communication can be modeled by linear systems. \[\]

• Time-variant and Time-invariant Systems
  A system is time-variant if its input and output relationship varies with time. The equations that define these classes are as follows: when \(y(n, t) = T[x(n-t)] = \mbox{input change}\) and \(y(n - t) = \mbox{output change}\), \[\begin{align} y(n, t) &= y(n-t) \ \ \mbox{for time-invariant systems}\\ y(n, t) &\neq y(n-t) \ \ \mbox{for time-variant systems}. \end{align}\] Time-variant systems are interesting to study because its output depends more on time because the system itself changes over time. The human vocal chords are time-variant because the vocal organs change as the tongue and the velum move. Time-invariant systems are much easier to reason about and model. \[\]

• Linear Time-variant and Linear Time-invariant Systems
  A linear time-invariant system, or LTI System, is one that is both linear and time-invariant. These systems are extremely important in the field of systems. This is because these systems can be analyzed mathematically so that output properties can be understood for any input signal. Also, they are compositional, so any combination of LTI systems is itself an LTI system. \[\]

• Static and Dynamic Systems
  Static systems are memory-less systems. An example equation for a static system might be \[y[t] = 2^{x[t]} .\] This is because the output at the current time step \(y[0]\) is dependent only on the input from the current time step \(x[t]\). On the other hand, a dynamic system (a system with memory) might have the following system equation: \[y[t] = 2 \cdot x[t - 1] .\] Here, the output at the current time step \(y[t]\) is 2 times the input from the previous time step \(x[t-1]\), so the system must remember that input. \[\]

• Causal and Non-causal Systems
  Similar to the distinction between static and dynamic systems, a causal system is one that depends on only present and past inputs. So, \(y[t] = 2 \cdot x[t - 1]\) still described a causal system. A non-causal system depends on future inputs. \(y[t] = x[t+1]\) is a non-causal system. \[\]

• Stable and Unstable Systems

  • A stable system is one that has bounded outputs for bounded inputs. In other words, for a bounded signal, the output amplitude is finite. So, the system described by \(y[n] = 2 \cdot x[n]\) is stable.
  • An unstable system has an unbounded output for a bounded input. These systems, when implemented correctly, will cause a stack overflow in computer programs.

Systems can be operated on and combined just like the signals they use. Cascading two systems, for example, combined two systems in a simple way. Cascading system \(S_0\) with \(S_1\) lets the output of \(S_0\), \(Y\), be the input for \(S_1\), \(W\). This operation is commutative as long as both systems are initially at rest (equal to 0). So, if the original systems have system functions

\[\begin{align} S_0\mbox{ : }Y &= \Phi_1 X \\ S_1\mbox{ : }Z &= \Phi_2 W, \end{align}\]

then we set the equation for \(S_0\) equal to the input for \(S_1\). So,

\[S_1\mbox{ : }Z = \Phi_2 \cdot \Phi_1 X.\]

Parallel addition is another way to combine systems. Let's say \(S_0\) has the equation \(Y = \Phi_1X\), and \(S_1\) has the equation \(Z = \Phi_2X\). It's important that the input signal is the same for this operation. So, the addition of these two output signals will simply be

\[W = (\Phi_1 + \Phi_2)X ,\]

where \(W\) is the summed output of the two systems.

There are 3 systems:

\[\begin{align} S_0\mbox{ : }A &= \Phi_1X \\ S_1\mbox{ : }B &= \Phi_2X \\ S_2\mbox{ : }C &= \Phi_3W. \end{align}\]

You add \(S_0\) and \(S_1\) and cascade the resulting system with \(S_2\). What is the output of these systems configured in this way?

Show Answer

The output, \(Z\), is

\[Z = \Phi_3(\Phi_2 + \Phi_1)X .\]

1. Bj, R. Discrete-time Signal. Retrieved June 14, 2016, from https://en.wikipedia.org/wiki/Discrete-time_signal
2. 1, Q. Even and Odd Function. Retrieved June 27, 2016, from https://en.wikipedia.org/wiki/Even_and_odd_functions
3. McDonald, A. Feedforward. Retrieved June 14, 2016, from https://en.wikipedia.org/wiki/Feed_forward_(control)