Supply and Demand
Supply and demand (sometimes called the "law of supply and demand") are two primary forces in markets. The concept of supply and demand is an economic model to represent these forces. This model reveals the equilibrium price for a given product, the point where consumer demand for a good at various prices meets the price suppliers are willing to accept to produce the desired quantity of that good. Supply and demand graphs help show why prices rise quickly for apartments in markets where there is a lot of demand (but little supply!), like San Francisco; or how prices for a good like oil can fall when refiners discover new oil deposits, increase production, or release millions of barrels of crude oil they held in reserve. But supply and demand graphs are not only limited to prices, they can represent decreases in wages when there is high unemployment, why some restaurants are booked out months in advance, or how interest rates affect the supply of money.
 A basic graph of supply and demand for some good, with the equilibrium point being the place where there the price, \(p\), that consumers are willing to pay matches the quantity of that good, \(q\), suppliers are willing to distribute at that price.
A basic graph of supply and demand for some good, with the equilibrium point being the place where there the price, \(p\), that consumers are willing to pay matches the quantity of that good, \(q\), suppliers are willing to distribute at that price.
Contents
Supply
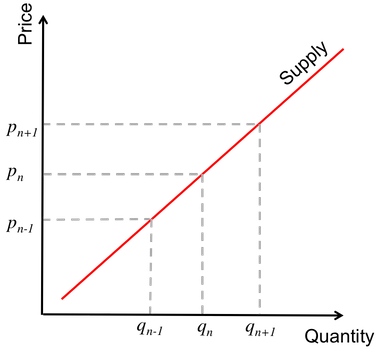 The representation between price and quantity suppliers are willing to provide
In microeconomic representations of supply and demand, supply typically represents suppliers or producers in the market. They have a decision to make about how to price their good to maximize profit, but also want to respond to changes in consumer demand. Because of this, the quantity of a good supplied has a direct relationship to the price suppliers can demand. The more consumers are willing to pay, the more product a supplier would be willing to provide. In the graph, if suppliers can demand a price increase of \(p_{n+1}\) then they'd be willing to supply more of the good, \(q_{n+1}\), assuming there are no constraints.
The representation between price and quantity suppliers are willing to provide
In microeconomic representations of supply and demand, supply typically represents suppliers or producers in the market. They have a decision to make about how to price their good to maximize profit, but also want to respond to changes in consumer demand. Because of this, the quantity of a good supplied has a direct relationship to the price suppliers can demand. The more consumers are willing to pay, the more product a supplier would be willing to provide. In the graph, if suppliers can demand a price increase of \(p_{n+1}\) then they'd be willing to supply more of the good, \(q_{n+1}\), assuming there are no constraints.
Supply is sometimes said to reflect the marginal costs, meaning the cost of producing one more unit of a good. The reason that increases in price can drive increases in supply is a confluence of factors, including: at higher prices increases in underlying costs of goods sold become less relevant, more competitors are willing to enter the market because they can profit more from producing this good than selling other goods, and, sometimes, because suppliers will have better expectations for the future as the price goes up. Declining prices can cause suppliers to believe that the good will continue to decline in price and cause them to lower production because of this expectation.
Demand
 The relationship between price and quantity demanded on the demand curve
In microeconomic representations of supply and demand, demand typically represents consumers in the market. It represents the cohort of people or organizations buying the good or service. In the law of supply and demand, the law of demand says that there is an inverse relationship between price and demand: as price increases, demand decreases, and vice versa. In the graph to the right, as the quantity \(q_n\) increases to \(q_{n+1},\) prices go down to \(p_{n-1}\). Or, as the price increases to \(p_{n+1},\) the quantity demanded by consumers decreases to \(q_{n-1}\). This is somewhat intuitive. When seasonal food items, like apples, are in season, the price goes down and consumers purchase and consume more apples; when the price goes up, consumers purchase fewer apples. This is especially true for products where there are substitute goods, like apples where consumers might switch to pears, bananas, or other fruits.
The relationship between price and quantity demanded on the demand curve
In microeconomic representations of supply and demand, demand typically represents consumers in the market. It represents the cohort of people or organizations buying the good or service. In the law of supply and demand, the law of demand says that there is an inverse relationship between price and demand: as price increases, demand decreases, and vice versa. In the graph to the right, as the quantity \(q_n\) increases to \(q_{n+1},\) prices go down to \(p_{n-1}\). Or, as the price increases to \(p_{n+1},\) the quantity demanded by consumers decreases to \(q_{n-1}\). This is somewhat intuitive. When seasonal food items, like apples, are in season, the price goes down and consumers purchase and consume more apples; when the price goes up, consumers purchase fewer apples. This is especially true for products where there are substitute goods, like apples where consumers might switch to pears, bananas, or other fruits.
Calculating Profit
One way firms determine how to price their goods is to look at the demand curve and calculate the potential revenue and profit at various prices and quantities:
\[(\text{Revenue}) = (\text{Quantity Sold}) \times (\text{Price}).\]
Suppose you're the head of some company selling widgets. Your team comes up with a new widget and is looking to price the product. An analyst on your team hands you the following graph of consumer demand for your widget. Which price is best to maximize revenue?
 The calculation here is pretty straightforward: \(q \times p = \text{revenue}\). At the lowest price, that's \(\$2.00 \times 200 = \$400\), and at the highest price it's \(\$5.00 \times 90 = \$450\). In between those prices, \(\$3.00\) turns out to be the optimal price to maximize revenue: \(\$3.00 \times 160 = \$480\). \(_\square\)
The calculation here is pretty straightforward: \(q \times p = \text{revenue}\). At the lowest price, that's \(\$2.00 \times 200 = \$400\), and at the highest price it's \(\$5.00 \times 90 = \$450\). In between those prices, \(\$3.00\) turns out to be the optimal price to maximize revenue: \(\$3.00 \times 160 = \$480\). \(_\square\)
However, that's not the end of the story. Companies often don't want to maximize revenue, but profit, the $ they get after costs:
\[\text{Profit} = \text{Revenue} - \text{Cost}. \]
Suppose you're still the head of a widget company and, in addition to the graph above, you're handed the below chart. This chart details the cost of goods sold for each widget based on the quantity sold. This varies because your widget incurs both fixed costs like the cost of keeping the lights on in the factory and variable costs like the cost of steel in each widget produced. It's also because your suppliers charge different prices for the raw materials you purchase based on quantity purchased.
Quantity Produced COGS 90 $2.90 115 $2.40 160 $2.00 200 $1.80 Now, which price point allows your company the greatest profit?
In this case you have to calculate both revenue and costs, to determine profit.
Price Quantity Produced COGS Revenue Total Cost Profit $5.00 90 $2.90 $450 $261 $189 $4.00 115 $2.40 $460 $276 $184 $3.00 160 $2.00 $480 $320 $160 $2.00 200 $1.80 $400 $360 $40 Even though pricing the product at $3.00 would generate more revenue, a price of $5.00 generates the most profit. This, actually, partially explains the existence of high margin luxury products that few can afford. Designer goods can command 80% or greater margins because they're charging high prices that few buy, but generate more profit than if they sold their goods to the masses.
Graphing Supply and Demand

The typical graph of supply and demand has price on the \(y\)-axis and quantity on the \(x\)-axis, with both supply and demand represented not as linear functions, but as polynomial functions, generally referred to as supply and demand curves. Sometimes, these curves can represent the supply curve of an individual firm, or the demand curve of an individual consumer, but generally economists use these curves to represent the cumulative supply and demand of multiple firms and consumers.
Supply and demand graphs do not remain static; shifts in underlying factors can cause the supply and demand curves to move. For instance, decreases in raw materials will decrease the supply of goods that depend on those materials, increasing price. In the graph to the right, the supply curve shifts up, increasing the price to \(p_2\) and decreasing the quantity to \(q_2\).
Suppose it's winter, and there is an ice storm in Florida, affecting the orange crop. Which of these graphs represents the most likely change in supply and demand for orange juice throughout the US?
 A - Demand shifts right, prices increase
A - Demand shifts right, prices increase
 B - Supply shifts left, prices increase
B - Supply shifts left, prices increase
 C - Supply shifts right, prices decrease
C - Supply shifts right, prices decrease
 D - Demand shifts left, prices decrease
D - Demand shifts left, prices decrease
These curves can be represented as linear or polynomial functions, typically in the form \(Q_s = (\text{intercept}) + (\text{slope} \times p) \) and \(Q_d = (\text{intercept}) + (\text{slope} \times p)\) for linear functions, or \(p^2\) for polynomial ones. Sometimes economists will approximate sections of a polynomial curve with a linear function for simplicity. Generally, though, these equations are represented as functions of the price. The equilibrium point is the point at which they're equivalent, \(Q_s = Q_d\).
Factors Affecting Supply and Demand, and the Equilibrium Price
Substitute Goods - Some products can easily be exchanged for another similar product: for instance, one brand \(A\) of bottled water versus another brand \(B\) of bottled water. In such situations, increases in the price of one good, \(A,\) may have a significantly non-linear affect on demand for that product. Consumers shopping in the grocery store may simply switch from \(A\) to \(B,\) causing quantity demanded of \(A\) to plummet.
Complementary Goods - Not to be mistaken with substitute goods, complementary goods are those products whose demand is tied to the demand of another product. For instance, bikes and bike helmets: the more bikes that are sold, the more demand for bike helmets is likely to happen.
Income - At different points in time consumers have more or less income and wealth and are, therefore, more or less able to demand goods, particularly luxury, non-necessary goods. Changes in the macroeconomics of a country can significantly affect demand of individual products. When the US economy went into recession in 2008, auto sales declined, even though the recession was caused by the crash of sub-prime mortgages.
Consumer Preferences and Expectations - For some industries more than others, trends and fashions drive demand. As such, the equilibrium price will shift heavily, based on a product being "in-fashion". For instance, various non-staple foods--coconut water, Greek yogurt, craft beer--all experienced increases in demand within the last decade, because of the trendiness of these products. Further, consumers' expectations about prices have significant effects on demand. Sales of the iPhone decline in the weeks leading up to a new iPhone launch, as consumers either wait for the new product or expect that prices on the previous models will decrease.
Suppose that tea and coffee are substitute goods. Suppose further that some modern version of the Boston Tea Party reoccurs and the supply of tea decreases significantly.

What's the effect on the supply and demand curve for coffee? What would a graph look like (assuming linear formula for supply and demand)?
Demand for coffee would rise, increasing prices from \(p_1\) to \(p_2\) and quantity from \(q_1\) to \(q_2\).
Marginal Costs and Elasticity
As the price of goods change, the quantity demanded changes. For instance, when shoes are on sale, at Buy One pair Get One pair free (essentially half-off), customers buy more shoes. But not just more, they buy more than double the quantity of shoes they would have if the shoes weren't on sale. Above, conditions like a consumer's income were said to be one of the causes of this behavior. But the measure of this behavior, the changes in demand, is known as the elasticity of demand. It's also possible for the rate of supply to change, and that's referred to as the elasticity of supply.
Generally, elasticity is a measure of the rate of change. In the case of the elasticity of demand, this can be calculated as
\[(\text{Price Elasticity of Demand}) = \frac{(\text{Change in Quantity Demanded})}{(\text{Change in Price})}.\]
For supply this is
\[(\text{Price Elasticity of Supply}) = \frac{(\text{Change in Quantity Supplied})}{(\text{Change in Price})}.\]
Essentially, elasticity is the linear slope.
 This graph displays the relationship between price and quantity demanded for gallons of orange juice.
The change in price that a consumer is willing to pay with each single change in unit demanded is called the marginal benefit, referring to the incremental benefit that that consumer gets from consuming \(1\) more unit. For instance, in the graph to the right, a consumer gains \(\$3.50\) more of benefit from shifting from \(1\) to \(2\) gallons of orange juice. That consumer is willing to pay a total of \(\$2.75\) for \(3\) gallons. This consumer is willing to pay less and less for each incremental unit, and this trend is referred to as diminishing marginal utility, the notion that, at a certain point, each additional unit's benefit is less and less. A thirsty person will gladly pay for a gallon of juice, but gains less and less benefit for \(2\) gallons, \(3\) gallons, \(4\) gallons, etc.
This graph displays the relationship between price and quantity demanded for gallons of orange juice.
The change in price that a consumer is willing to pay with each single change in unit demanded is called the marginal benefit, referring to the incremental benefit that that consumer gets from consuming \(1\) more unit. For instance, in the graph to the right, a consumer gains \(\$3.50\) more of benefit from shifting from \(1\) to \(2\) gallons of orange juice. That consumer is willing to pay a total of \(\$2.75\) for \(3\) gallons. This consumer is willing to pay less and less for each incremental unit, and this trend is referred to as diminishing marginal utility, the notion that, at a certain point, each additional unit's benefit is less and less. A thirsty person will gladly pay for a gallon of juice, but gains less and less benefit for \(2\) gallons, \(3\) gallons, \(4\) gallons, etc.
What is the elasticity of the curve to the right, when shifting from \(1\) to \(2\) gallons?
We have\[\begin{align} (\text{Price Elasticity of Demand}) &= \frac{(\text{Change in Quantity Demanded})}{(\text{Change in Price})}\\ &= \frac{\frac{1}{1}}{\frac{\$2.00}{\$5.50}} = \frac{1}{0.\overline{36}} = 2.75. \end{align}\]
As a bonus, the elasticity between 2 and 3 gallons is \(\frac{\frac{1}{2}}{\frac{\$0.75}{\$3.50}} = \frac{7}{3} = 2.\overline{33}.\)
Demand and supply are said to be elastic when the elasticity is greater than \(1\), meaning that the rate of quantity changes more than rate of price changes. If it's less than \(1\) they are said to be inelastic, and \(1\) exactly is said to be perfect inelastic and is a straight line.
 A supply curve for gallons of orange juice produced at various prices
However, elasticity can also change, and changing elasticity is the reason why the demand and supply curves are said to be "curves" and not linear lines. In the graph to the right, marginal costs at low quantities shipped, for instance \(100\) or \(150\) gallons, have high supply elasticities \((>1).\) To produce these \(50\) more creates (an increase of 50%) only requires an increase in price of \(\$0.05\) per gallon (4%). But the elasticity at high prices is less than 1, with a change between a \($4.30\) price and a \($5.10\) price only increasing quantity supplied by \(10\) gallons.
A supply curve for gallons of orange juice produced at various prices
However, elasticity can also change, and changing elasticity is the reason why the demand and supply curves are said to be "curves" and not linear lines. In the graph to the right, marginal costs at low quantities shipped, for instance \(100\) or \(150\) gallons, have high supply elasticities \((>1).\) To produce these \(50\) more creates (an increase of 50%) only requires an increase in price of \(\$0.05\) per gallon (4%). But the elasticity at high prices is less than 1, with a change between a \($4.30\) price and a \($5.10\) price only increasing quantity supplied by \(10\) gallons.
This graph also demonstrates diminishing marginal utility, the notion that, at a certain point, each additional unit costs so much more to produce that the utility from producing that unit is lower and lower each time.