Tangent to Circles - Problem Solving

One tangent line, and only one, can be drawn to any point on the circumference of a circle, and this tangent is perpendicular to the radius through the point of contact. In the figure below, line \(BC\) is tangent to the circle at point \(A\).

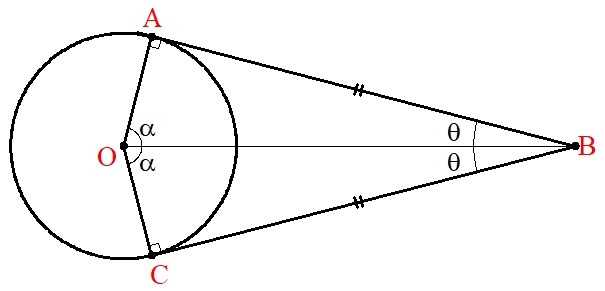
If two tangents are drawn to a circle from an external point,

• the lengths of the tangents from the external point to the points of contact are equal;
• they subtend equal angles at the center of the circle.

In the figure below, \(AB=CB, \angle AOB= \angle COB\) and \(\angle ABO=\angle CBO\).

In the figure below, \(BA\) and \(BC\) are tangents to the circle at points \(A\) and \(C\), respectively. If \(\angle AEC=110^\circ\) and \(\angle DCE=80^\circ\), find \(\angle ABC\).

---

SOLUTION

Consider the diagram to the right.

• Opposite angles of a cyclic quadrilateral sum up to \(180^\circ\). So \[\angle ADC=180^\circ-110^\circ=70^\circ.\]
• From the inscribed angle theorem, we can see that \[\angle AOC=2 \angle ADC=2(70^\circ)=140^\circ.\]

Since the sum of interior angle of a quadrilateral is \(360^\circ\), we have \[\begin{align} \angle ABC &=360^\circ-\angle BCO-\angle BAO-\angle AOC\\ &=360^\circ-90^\circ-90^\circ-140^\circ\\ &=40^\circ.\ _\square \end{align}\]

Submit your answer

In the figure to the right, the yellow circle is tangent to \( \triangle ABC \) at points \( D, E, F. \)

\( 2 \sqrt{14}, 4 \sqrt{3}, \) and \( \sqrt{42} \) are the lengths of the common tangents to the semicircles of diameters \((BD, CD), (CE, AE),\) and \((AF, BF),\) respectively.

What is the radius of the yellow circle?

Submit your answer

In the diagram below, line segments \(STM\) and \(MQ\) are tangents to the circle at \(T\) and \(Q,\) respectively. \(C\) is the center of the circle and does not lie on \(QS.\) If \(SRQ\) is a straight line, \(SR=TR,\) and \(\angle TSR=25^\circ,\) what is \(\angle QMT\) in degrees?