Transience and Recurrence of Markov Chains
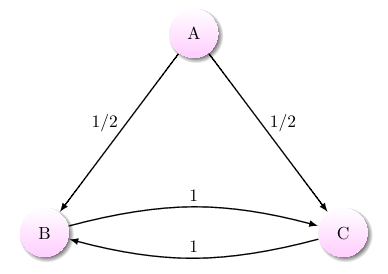A Markov chain with one transient state and two recurrent states
A stochastic process contains states that may be either transient or recurrent; transience and recurrence describe the likelihood of a process beginning in some state of returning to that particular state. There is some possibility (a nonzero probability) that a process beginning in a transient state will never return to that state. There is a guarantee that a process beginning in a recurrent state will return to that state.
Transience and recurrence issues are central to the study of Markov chains and help describe the Markov chain's overall structure. The presence of many transient states may suggest that the Markov chain is absorbing, and a strong form of recurrence is necessary in an ergodic Markov chain.
In a Markov chain, there is probability \(1\) of eventually (after some number of steps) returning to state \(x\). Must the expected number of returns to state \(x\) be infinite?
Yes!
In a Markov chain, there is probability \(1\) of eventually (after some number of steps) returning to state \(x\). Must the expected number of steps to return to state \(x\) be finite?
No!
Equivalent Definitions
Intuitively, transience attempts to capture how "connected" a state is to the entirety of the Markov chain. If there is a possibility of leaving the state and never returning, then the state is not very connected at all, so it is known as transient. In addition to the traditional definition regarding probability of return, there are other equivalent definitions of transient states.
Let \(\{X_0, \, X_1, \, \dots\}\) be a Markov chain with state space \(S\). The following conditions are equivalent.
- A state \(i \in S\) is transient.
- Let \(T_i = \text{min}\{n \ge 1 \mid X_n = i\}\) . Then, \( \mathbb{P}(T_i < \infty \mid X_0 = i) < 1.\)
- The following sum converges: \( \displaystyle\sum_{n = 1}^\infty \mathbb{P}(X_n = i \mid X_0 = i) < \infty.\)
- \( \mathbb{P}(X_n = i \text{ for infinitely many } n \mid X_0 = i) = 0.\)
Similarly, a classification exists for recurrent states as well.
Let \(\{X_0, \, X_1, \, \dots\}\) be a Markov chain with state space \(S\). The following conditions are equivalent.
- A state \(i \in S\) is recurrent.
- Let \(T_i = \text{min}\{n \ge 1 \mid X_n = i\}\) . Then, \( \mathbb{P}(T_i < \infty \mid X_0 = i) =1.\)
- The following sum diverges: \( \displaystyle\sum_{n = 1}^\infty \mathbb{P}(X_n = i \mid X_0 = i) = \infty.\)
- \( \mathbb{P}(X_n = i \text{ for infinitely many } n \mid X_0 = i) = 1.\)
Positive vs Null Recurrent
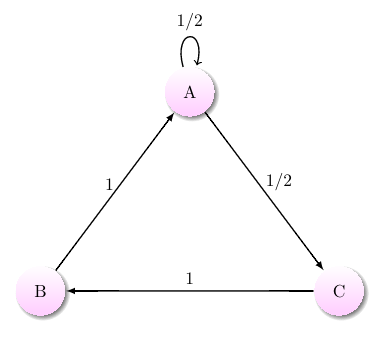An aperiodic Markov chain with positive recurrent states
While a recurrent state has the property that the Markov chain is expected to return to the state an infinite number of times, the Markov chain is not necessarily expected to return even once within a finite number of steps. This is not good, as a lot of the intuition for recurrence comes from assuming that it will. In order to fix that, there is a further classification of recurrence states.
Let \(T_i = \text{min}\{n \ge 1 \mid X_n = i\}\) be the time of the first return to \(i\). Then, the expected value \(\mathbb{E}(T_i \mid X_0 = i)\) is the property discussed above.
- A state \(i\) is known as positive recurrent if \(\mathbb{E}(T_i \mid X_0 = i) < \infty\).
- A state \(i\) is known as null recurrent if \(\mathbb{E}(T_i \mid X_0 = i) = \infty\).
If a state is periodic, it is positive recurrent. However, as shown to the right, there exist plenty of aperiodic Markov chains with only positive recurrent states.
The following is a depiction of the Markov chain known as a random walk with reflection at zero.
\(p + q = 1\)
With \(p < \tfrac{1}{2}\), all states in the Markov chain are positive recurrent. With \(p = \tfrac{1}{2}\), all states in the Markov chain are null recurrent. With \(p > \tfrac{1}{2}\), all states in the Markov chain are transient.