Waves

In physics, a wave is an oscillating disturbance of some physical quantity in space and periodic in time. A wave is accompanied by a transfer of energy that travels through space or mass. The space is characterized by oscillation wavelength and the elapsed time is measured by an oscillation wave period which is the inverse of the frequency. These two quantities are related by the speed of wave propagation.

Physically, a wave is an energy pulse that propagates through space or through a (liquid, solid or gaseous ) medium with a defined speed. According to what some researchers observed until now, nothing prevents a magnetic wave to propagate in vacuum or through the material, as in the case of electromagnetic waves in vacuum or through the neutrino material, where the particles of the medium oscillate around a point average but do not move. Except for electromagnetic radiation, and probably gravitational waves, which can propagate through a vacuum, waves exist in a medium whose deformation is capable of producing restoration forces through which they travel and can transfer energy from one place to another without any particulate medium begin moved, i.e. the wave does not transport matter. However, there are always fluctuations associated with the propagation medium. A wave is longitudinal when the oscillation occurs in the direction of propagation, or cross when the oscillation occurs in the direction perpendicular to the direction of wave propagation.

Waves

We classify media where waves can propagate in the following ways:

• linear medium: different waves of any particular point of the medium in question can be added;

• limited means: if it is finite in extent, otherwise they are considered unlimited;

• means uniform : if its physical properties can not be modified in different points;

• isotropic media : if its physical properties are the same in any direction.

Examples of Waves:

• Ocean surface waves, which are perturbations that propagate through water (see also surfing and tsunami).

• Sound, a mechanical wave that propagates through gases, liquids and solids, which is a frequency detected by the auditory system. A similar seismic wave is present in the earthquake wave, which may be of types S, P and L.

• Light, radio waves, X-ray, etc. are electromagnetic waves. In this case the propagation is possible through a vacuum.

All waves have common behavior patterns in situations, which can be summarized as the following characteristics:

• Reflection: When a wave is back to the direction where it came from, due to hit in reflective material.
• Refraction: The change of the direction of the waves due to entry into another medium. The wave velocity varies as the wavelength also varies, but the frequency remains always the same, which is characteristic of the emitting source.
• Diffraction: Scattering waves, for example, when crossing a slit equivalent to its wavelength size. High waves with wavelength are diffracted easily .
• Interference: Addition or subtraction of the amplitudes of the waves depends on the phase of the waves in the superposition occurs.
• Dispersion: The separation of a wave at other different frequencies.
• Vibration: Some waves are produced by vibrating objects, producing sounds. Example are strings (guitar, violin, piano, etc.) or tubes (organ, flute, trumpet, trombone, saxophone, etc.).
• Polarization: The wave may be polarized by using a polarizing filter. The polarization of a transverse wave describes the direction of oscillation in the plane perpendicular to the direction of travel. Longitudinal waves such as sound waves have no polarization. For these waves the direction of oscillation is along the direction of travel .

Sine wave entering a region of lower velocity, showing refraction

• $1 =$ Elements of a wave
• $2 =$ Distance
• $3 =$ Offset
• $\lambda =$ Wavelength
• $\gamma  =$ Amplitude (Amplitude is a scalar positive and negative measure of the amplitude of an oscillation wavelength. The distance $y$ is the amplitude of the wave.)

Waves can be described using a number of variables, including the frequency, width and height of the wave, amplitude and period. The amplitude of a wave is a measure of the magnitude of a disturbance in a medium during one cycle of the waveform. For example, waves on a string have their amplitude expressed as a distance (meters), sound waves as pressure (pascals) and electromagnetic waves as the amplitude of the electric field (volts per meter). The amplitude may be constant (in this case the wave is a continuous wave) or may vary with time and/or position. The form of this variation is the envelope of the wave. The period is the time $(T)$ of a complete cycle of an oscillation of a wave. The frequency $(F)$ period is divided by a unit of time (example: one second), and is expressed in hertz. See below: $$F=\dfrac{1}{T}.$$ When the waves are expressed mathematically, the angular frequency (omega; radians per second) is constantly used, in connection with frequency $F$: $$F= \dfrac{\omega}{2 \pi}.$$

$$$$ Standing Waves and Non-stationary Waves:

Waves that remain in place are called paranticas waves, like vibrations on a violin string.

When a rope is deformed, the disturbance propagates throughout the cord, reflected in their fixed ends. The interference of several waves could result in a standing wave, or oscillation that appears not to move through the material. Nodes are caused by interference (destructive) between the crest of two waves and belly. In the antinodes, where the offset is maximum, interference occurs between two crests and two wave antinodes. Each oscillation pattern corresponds to a particular frequency to what is called a harmonic. The vibration frequencies vary with the length of the string and its characteristics (material, tension, thickness), which determine the speed of propagation of waves. At the lowest concentration at which the string vibrates is called the fundamental frequency.

Waves moving (non-stationary) have a disturbance that varies both with time $t$ as the distance $z$ can be expressed mathematically as

$$y=A(z,t)\cdot\cos(kz-\omega t+\phi),$$

where $A (z, t)$ is the amplitude envelope of the wave, $k$ is the wave number, and $\phi$ is the phase constant. The velocity $v$ of this wave is given by

$$v= \frac{\omega}{k}= \lambda f,$$

where $\lambda$ is the wavelength .

$$$$ The Universal Wave Equation

The simplest form of this equation Is

$$\nu= \lambda f,$$

where

• $v$: speed of the wave
• $\lambda$: wavelength
• $f$: frequency of the wave.

• One-dimensional Waves: those that propagate in a single direction, e.g. waves on strings

• Two-dimensional Waves: those that propagate in a plane, e.g. waves on the surface of a lake or pond

~

• Two-dimensional Wave on a Disc in general:

• A wave on a disk with two nodal lines crossing in the center, which is a harmonic sound

• Three-dimensional Waves (3D)

• Those that propagate in all directions, e.g. sound waves in the atmosphere or metals

$$$$ What Is sound?

The sound propagation front of a mechanical or mechanical compression wave; this wave propagates circuncêntrica way, only in material resources - they have mass and elasticity such as solid, liquid or gaseous, i.e. does not propagate in a vacuum.

The natural sounds are mostly combinations of signals but a monotonic pure sound, represented by a pure sinusoid, an oscillation velocity or frequency is measured in hertz (Hz) and an amplitude or energy measured in decibels. The audible sound by the human ear has a frequency between 20 Hz and 20 kHz. Above and below this range are ultrasound and infrasound, respectively.

Humans and many animals perceive sounds with the sense of hearing with two ears, which lets you know the distance and position of the sound source: a call stereophonic hearing. Many low-frequency sounds can also be felt in other parts of the body and research shows that elephants communicate via infrasound.

The sounds are used in various ways, especially in speech, communication, or music. The perception of sound can also be used to acquire information about the environment properties as spatial characteristics (shape, topography) and the presence of other animals or objects. For example, bats, whales, and dolphins use echolocation to fly and swim through obstacles and hunt their prey. Ships and submarines use sonar; humans receive and use spatial information perceived in sounds.

The chart below represents a wave that propagates with a speed of 300 m/s.

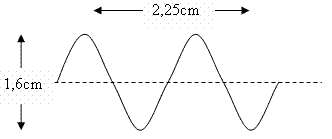
a) Determine the amplitude of the wave.

b) Determine the wavelength.

c) Determine the frequency.

d) Determine the period.

---

a) The amplitude of the wave is given by the distance from the origin to the crest of the wave: $$A= \dfrac{1.6}{2} = 0.8 \text{ (cm)}.$$

b) The wavelength is given by the distance between two crests or nodes 3, namely, as the figure shows the extent of three "half-wavelength," we can calculate it as follows: $$\begin{aligned} \dfrac{3\lambda}2&=2.25\\ \Rightarrow \lambda&=\dfrac{2.25}3\cdot 2\\ &=1.5 \text{ (cm)}. \end{aligned}$$

c) Knowing the speed of propagation and wavelength, we can calculate the frequency using the equation $$v= \lambda f ~\text{ or }~ f=\dfrac{v}{\lambda}.$$ Substituting the values ​​into the equation, $$f= \dfrac{300 \text{ km/s} }{0.015 \text{ m}} = 20000\text{ Hz}.$$

d) As the period is equal to the inverse of frequency, $$T= \dfrac{1}{f}=\frac{1}{20000} = 5 \cdot 10^{-5}\text{ (s)}. \ _\square$$

A wireless router emits electromagnetic waves with a frequency of 5.0 GHz. It is also known that the speed of propagation of this wave in the air is equal to the speed of light in vacuum (c = 300,000 km/s). Calculate the value of $\lambda$ wavelength, in meters, for this wave.

---

The propagation velocity of a wave is given by: $v= \lambda f$. But see $$\begin{aligned} v = c &= 3 00, 000\text{ km/s} \\ &= 3 00, 000, 000\text{ m/s} \\ &= 3 \times 10^8 \text{ m/s}\\ f &= 5\text{ GHz} = 5.10^9 \text{ Hz}. \end{aligned}$$ Therefore, $$\lambda = \dfrac{v}{f} = \dfrac{3}{5} \times 10^ {-1}\text{ m} = 0.06\text{ m}. \ _\square$$

Here are some equations to help you!