When Does A Limit Exist?
The limit of a function is a fundamental concept in calculus. When the limit exists, the definition of a limit and its basic properties are tools that can be used to compute it. The focus of this wiki will be on ways in which the limit of a function can fail to exist at a given point, even when the function is defined in a neighborhood of the point.
Contents
One-sided Limits are Different
A common situation where the limit of a function does not exist is when the one-sided limits exist and are not equal: the function "jumps" at the point.
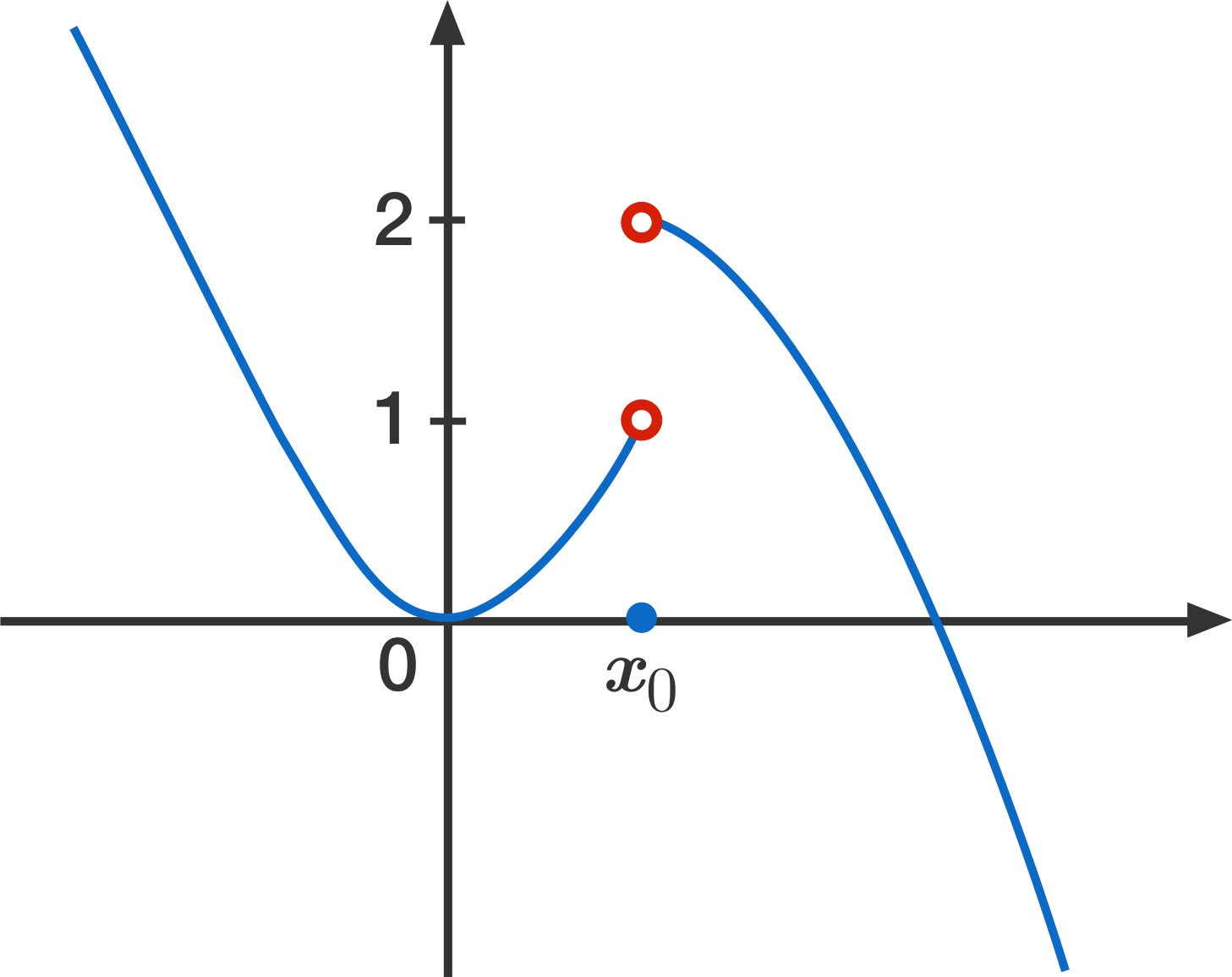 The limit of \(f\) at \(x_0\) does not exist. [1]
The limit of \(f\) at \(x_0\) does not exist. [1]
For the function \(f\) in the picture, the one-sided limits \( \lim\limits_{x\to x_0^-} f(x)\) and \( \lim\limits_{x\to x_0^+} f(x)\) both exist, but they are not the same, which is a requirement for the (two-sided) limit to exist. This is usually written
\[\lim_{x \to x_0} f(x) = \text{DNE},\]
where "DNE" stands for "does not exist."
Select one or more
Let \(\displaystyle f(x) = \frac{x^2-9x+20}{x-\lfloor x \rfloor},\) then which of the following are correct?
Notation: \( \lfloor \cdot \rfloor \) denotes the floor function.
The Function "Blows up"
Another common situation when limits do not exist involves the function "blowing up" to \(\infty\) or \(-\infty.\) The graph is characterized by a vertical asymptote at \( x=0:\)
 The one-sided limits of \(f(x) = \frac1x\) at \(x=0\) do not exist. [2]
The one-sided limits of \(f(x) = \frac1x\) at \(x=0\) do not exist. [2]
While it is correct to say that \( \lim\limits_{x\to 0^-} \frac1{x} \) and \( \lim\limits_{x\to 0^+} \frac1{x} \) do not exist, in this case the limits are generally written as
\[\lim_{x\to 0^-} \frac1{x} = -\infty \qquad \text{ and }\qquad \lim_{x\to 0^+} \frac1{x} = \infty.\]
This is the standard notation that has the benefit of being more specific about the way in which these limits fail to exist. For the formal definitions, see the infinite limits section.
When the one-sided limits blow up in the same way, this can be shortened to a single two-sided limit, e.g.
\[\lim_{x\to 0^-} \frac1{x^2} =\infty \qquad \text{ and }\qquad \lim_{x\to 0^+} \frac1{x^2} = \infty.\]
So,
\[\lim_{x\to 0} \frac1{x^2} = \infty,\]
but it should be emphasized that \( \lim\limits_{x\to 0} \frac1{x^2} \) does not exist; saying that it "equals \(\infty\)" is just a way of describing why it does not exist.
Oscillatory Behavior
The third class of functions which give non-existent limits are the most exotic. If \(f\) does not jump or blow up at \( x_0\) but \( \lim\limits_{x\to x_0} f(x) \) does not exist, the general picture is that \(f\) takes on multiple values which are far away from each other, even when its argument moves closer and closer to \( x_0.\)
The standard example is \(f(x) = \sin \frac1x \) near \(x_0 = 0.\)
The function \(\sin \frac1x\) oscillates infinitely often as it approaches 0. [3]
If \( \lim\limits_{x\to 0^+} \sin \frac1x = L\) were true for some \( L,\) then the definition of limit would imply that there was an open interval \( (0,\delta) \) such that the values of \( \sin \frac1x\) for \( x\) in that interval were within, say, \( 0.1\) of \( L.\) But no matter how small \(\delta\) might be, it would have to contain \( x_1 = \frac1{2N\pi} \) and \( x_2 = \frac1{\big(2N+\frac12\big)\pi} \) for some sufficiently large \( N.\) Since \( \sin \frac1{x_1} = 0 \) and \( \sin \frac1{x_2} = 1,\) this is a contradiction.
\[ \begin{align} f(x) &= \begin{cases} 0 &\text{ if } x \text{ is irrational} \\ 1 &\text{ if } x \text{ is rational} \end{cases} \\ g(x) &= \begin{cases} 0 &\text{ if } x \text{ is irrational} \\ \frac1q &\text{ if } x =\frac{p}{q}, \text{ where } p \text{ and } q \text{ are coprime nonnegative integers} \end{cases} \end{align} \]
Let \( f(x) \) and \( g(x) \) be two functions defined on \( [0,1] \) by the formulas as described above.
For which \( a \in (0,1) \) does the (deleted) \( \lim\limits_{x\to a} f(x) \) exist?
For which \( b \in (0,1) \) does the (deleted) \( \lim\limits_{x\to b} g(x) \) exist?
Domain Considerations
It is worth emphasizing that the above examples are all of functions \(f\) that are defined at every point in an open interval around the point \( x_0\) in question, except possibly for \( x_0 \) itself. There are other examples of functions which do not have two-sided limits at \(x_0\) because this assumption fails.
\(\lim\limits_{x\to 0} \sqrt{x} \) does not exist for the simple reason that \( \sqrt{x} \) is not defined in any open interval containing \( 0,\) since its domain is \( [0,\infty).\)
\(x=0\) is an endpoint of the domain for \(f(x) = \sqrt{x}.\) [4]
References
- Alexandrov, O. Discontinuity. Retrieved September 12, 2005, from https://commons.wikimedia.org/wiki/File:Discontinuity_jump.eps.png
- Richards, G. Rectangular hyperbola. Retrieved July 2, 2008, from https://commons.wikimedia.org/wiki/File:Rectangular_hyperbola.svg
- Thoma, M. Sin(1/x). Retrieved September 18, 2012, from https://commons.wikimedia.org/wiki/File:Sin%281x%29.svg
- Richards, G. Square root. Retrieved July 2, 2008, from https://commons.wikimedia.org/wiki/File:Square_root_0_25.svg
