Geometric Probability

Geometric probability is a tool to deal with the problem of infinite outcomes by measuring the number of outcomes geometrically, in terms of length, area, or volume. In basic probability, we usually encounter problems that are "discrete" (e.g. the outcome of a dice roll; see probability by outcomes for more). However, some of the most interesting problems involve "continuous" variables (e.g., the arrival time of your bus).

Dealing with continuous variables can be tricky, but geometric probability provides a useful approach by allowing us to transform probability problems into geometry problems. If this sounds surprising, take a look at the following problem:

Your bus is coming at a random time between 12 pm and 1 pm. If you show up at 12:30 pm, how likely are you to catch the bus?

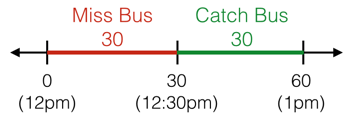
Intuitively, the answer seems to be \(\frac{1} {2} \). We can show this geometrically by considering a point chosen randomly on a 1-dimensional number line: the length of the number line between 12:30 pm and 1 pm is equal to the length from 12 pm to 12:30 pm.

While this example is fairly straightforward, many complicated problems can be solved simply by using geometric probability. On this page, we will start with 1D examples, which are the simplest and easy to understand and then work our way up to 2D, 3D, and higher dimensions.

One of the main ideas in probability is to count the number of equally likely "desired" outcomes, and then divide that by the number of equally likely total outcomes:

\[ P(X) = \frac{\mbox{desired outcomes}}{\mbox{total outcomes}} .\]

However, when a variable is continuous, it becomes impossible to "count" the outcomes in the traditional sense. For example, if \(X\) is a random real number between 0 and 1, it could be \(0.2\) or \(0.53\) or \(0.434662565465465\) or even something irrational like \(\frac{\pi}{4}.\) It is clear that there are infinite outcomes if we count in the traditional sense.

Let's look more at the situation where \(X\) is a random real number, as mentioned in the Introduction section.

\(X\) is a random real number between 0 and 3. What is the probability \(X\) is closer to 0 than it is to 1?

---

Since there are infinitely many possible outcomes for the value of \(X,\) we will take the equally likely outcomes as random points along the number line from 0 to 3. It’s easy to see that \(X\) will be closer to 0 than it is to 1 if \(X<0.5.\)

Probability line

Now, we can use the measures (lengths, in this 1D case) of our possible outcomes and apply the usual probability formula. Here,

\[P(X\text{ is closer to 0 than to 1}) = \frac{\mbox{length of segment where }0<X<0.5}{\mbox{length of segment where }0<X<3} = \frac{0.5}{3} = \frac{1}{6} \approx 17\%.\ _\square\]

To reiterate, the core idea in one-dimensional (1D) geometric probability is translating a probability question into a geometry problem on a number line, where we measure outcomes with length. To make sure you've got this concept down, try this problem related to rounding errors:

The reason as to why this works is a more advanced topic, which deals with the idea of measure theory. Measure theory gives a rigorous framework for probability theory, including probabilities on finite sets. Measure theory is also the key idea behind integration in calculus, and can be used to find integrals of functions that seem non-integrable using “standard” methods. These two ideas are not unrelated, as at a fundamental level, probability theory is just a special case of integration.

We will do a few more examples on working with geometric probabilities in higher dimensions to get a better feel for how to work with the concept. It is often helpful to use a figure to help with understanding and solving these types of problems.

Many probability problems include more than one variable, so 1D geometric probability won't be enough. For problems with two variables, it is often helpful to transform them into 2D geometric probability questions, where the outcomes are measured by area:

\[P(X) = \dfrac{\text{area of desired outcomes}}{\text{area of total outcomes}}.\]

This is most easily understood when the problem at hand is explicitly a 2D geometry problem:

A dart is thrown at a circular dartboard such that it will land randomly over the area of the dartboard. What is the probability that it lands closer to the center than to the edge?

---

The set of outcomes are all of the points on the dartboard, which make up an area of \(\pi r^2\) where \(r\) is the radius of the circle. The points that are closer to the center than to the edge are those that lie within the circle of radius \(\frac{r}{2}\) around the center, so the area of the "success" outcomes is \(\pi \left(\frac{r}{2}\right)^2 = \frac{\pi r^2}{4}.\)

Thus,

\[P(\text{closer to center than edge}) = \dfrac{\text{area of desired outcomes}}{\text{area of total outcomes}} = \frac{\frac{\pi r^2}{4}}{\pi r^2} = \frac{1}{4} = 25\%.\ _\square\]

A square \( S \) has side length 30. A standard 20-sided die is rolled, and a square \( T \) is constructed inside \( S \) with side length equal to the roll. Then, a dart is thrown and lands randomly somewhere inside square \( S \). What is the probability that the dart also lands inside square \( T ?\)

---

Suppose the die rolls \( i \). Then the probability that the dart will land inside square \( T \) is the ratio of the area of square \( T \) to the area of square \( S \). This is \( \frac{i^2}{900} \). For each \( i \), the probability that the die will roll \( i \) is \( \frac{1}{20}, \) so the probability that the dart lands inside \( T \) will be

\[ \sum\limits_{i=1}^{20} \frac{1}{20}\cdot \frac{i^2}{900} = \frac{1}{20} \cdot \frac{20 \times 21 \times 41}{900 \times 6} = \frac{287}{1800} . \ _\square\]

The difficulty associated with geometric probability usually comes from one of two areas: the first is finding a good way to model the problem geometrically, and the second is in trying to determine the areas/volumes of particular regions in order to calculate the relative probabilities. As in finite probability, it is sometimes simpler to find the probability of the complement.

To make sure you've got down the basic ideas of 2D geometric probability, try this similar question. Note that many 2D geometry problems, such as the one below, use the ideas of composite figures. If you are not familiar with that concept, you may want to take a look at composite figures first.

However, one of the most powerful uses of geometric probability is applying it to problems that are not inherently geometric. Identifying when and how to use geometric probability is never obvious, but a good sign is that you are dealing with probabilities in a situation with continuous variables. Let's take a look at a modified example of the bus problem mentioned at the beginning of this wiki.

Both the bus and you get to the bus stop at random times between 12 pm and 1 pm. When the bus arrives, it waits for 5 minutes before leaving. When you arrive, you wait for 20 minutes before leaving if the bus doesn't come. What is the probability that you catch the bus?

---

We have two continuous variables here: \(b,\) the time in minutes past 12 pm that the bus arrives, and \(y,\) the time in minutes past 12 pm that you arrive. Since there are 2 independent variables, we will convert this into a 2-dimensional geometry problem. Specifically, we can think of the set of all outcomes as the points in a square: Then, we need to determine the region of "success"; that is, the points where we catch the bus. Since the bus will wait for 5 minutes, you need to arrive within 5 minutes of the bus' arrival, or \(y \le b+5:\)

However, you only wait for 20 minutes, so you can't arrive more than 20 minutes before the bus, so \(y \ge b-20:\) Combining our two conditions, we have a region of success as shown below: Now, we just need to find the area of this success region. A simple method is to find the area of the non-success region, and then subtract that from the total area: Thus, the probability of catching the bus is

\[P(\text{catching the bus}) = \dfrac{\text{area of desired outcomes}}{\text{area of total outcomes}} = \frac{60^2 - \frac{55^2}{2}-\frac{40^2}{2}}{60^2} = \frac{103}{288} \approx 36\%.\ _\square\]

Now that we have changed our problem into a geometric one, we can easily answer other questions about the situation such as the following:

1) What is the probability that the bus does not have to wait for you?
2) What is the probability that you had to wait less than 10 minutes, given that you were able to catch the bus?
3) What is the probability that the bus came and went before you, given that you were not able to board the bus?

To practice these ideas, let's try a similar question:

At this point, you can probably guess where this is headed! 3D geometric probability is when we are dealing with 3 continuous variables, and we measure the volume of the various outcomes; that is,

\[P(X) = \dfrac{\text{volume of desired outcomes}}{\text{volume of total outcomes}}.\]

To get started, let's look at an example which is analogous to the first problem we solved in the 2D geometric probability section.

An atom is inside a sphere and it is equally likely to be anywhere within the sphere. What is the probability that it lands closer to the center of the sphere than the outside?

---

The set of outcomes are all of the points in the sphere, which make up a volume of \(\frac{4\pi}{3} r^3\) where \(r\) is the radius of the sphere. The points that are closer to the center than to the edge are those that lie within the sphere of radius \(\frac{r}{2}\) around the center, so the volume of the "success" outcomes is \(\frac{4\pi}{3} \left(\frac{r}{2}\right)^3 = \frac{\pi}{6}r^3.\) Thus,

\[P(\text{closer to center than outside}) = \dfrac{\text{volume of desired outcomes}}{\text{volume of total outcomes}} = \frac{\frac{\pi}{6}r^3}{\frac{4\pi}{3} r^3} = \frac{1}{8} = 12.5\%.\ _\square\]

Of course, not all problems will be so explicitly geometric in nature. As usual, one of the signs that we might want to apply geometric probability is that we are dealing with continuous variables. Let's see how we can approach the following example:

Alex, Bob, and Charlie each randomly pick a real number between 0 and 1. What is the probability that the sum of the squares of their numbers does not exceed 1?

---

First, if we let their 3 numbers be \(x,\) \(y,\) and \(z,\) it is easy to see that the outcomes can be represented as points within a unit cube \(\big(\)the cube that encloses the region \(x,y,z \in [0,1]\big),\) which has volume \(1^3 = 1.\)

Then, the region where the sum of the squares of their numbers does not exceed 1 is given by \(x^2+y^2+z^2 \le 1,\) which (without restriction) is the sphere of radius 1 centered around the origin \((0,0,0).\) However, since \(x,y,z\ge 0,\) exactly \(\left(\frac{1}{2}\right)^3 = \frac{1}{8}\) of this sphere (one "octant") lies within the unit cube of possible outcomes. Hence, the volume of this "success" region is \(\frac{1}{8} \cdot \left(\frac{4\pi}{3} \cdot 1^3\right) = \frac{\pi}{6}.\)

Thus,

\[P(\text{sum of squares does not exceed 1}) = \dfrac{\text{volume of desired outcomes}}{\text{volume of total outcomes}} = \frac{\frac{\pi}{6}}{1} = \frac{\pi}{6} = 52\%.\ _\square\]

If you'd like to test your skills at turning probability problems into 3D geometry problems, take a shot at this challenging problem which is similar to the example above:

In addition to being a useful mathematical problem-solving tool, geometric probability can also be applied in other scientific fields. Let's start with an example from mechanics, using the ideas of velocity and acceleration.

We are playing shuffleboard on the table below, where the lengths of the regions are labelled below (in meters).

You push the puck with initial velocity \(v,\) where \(v\) is randomly chosen between 5 and 15 meters/second. Since the table is rough, the puck decelerates at a constant rate of 5 m/s\(^2.\) What is the probability that you slide the puck off of the table? (You may assume that the puck is negligibly small.)

---

In this problem, we have only one variable--the initial speed of the puck--so this is going to be a 1-dimensional geometry problem. Recall the kinematics formula \( v_{f} ^{2} = v_{i}^{2} + 2 a s \). The final speed \(v_ {f }\) is zero because the puck comes to a rest. The initial speed \( v_{i} = v\). The distance traveled \(s\) will decide how many points we get. After plugging in the values, we get

\[s = \frac{ v^{ 2 } }{ 10 }, \]

so \(s>8+4+2+1=15\) occurs when \(v>\sqrt{150}.\) If we think of \(v\) as being a point on a number line between 5 and 15, then we can find our probability as

\[\frac{15-\sqrt{150}}{15-5} \approx 28\%.\ _\square\]

Awesome! Who would have expected that geometric probability would allow us to solve a physics problem? Let's check out a few more examples.

A block performs simple harmonic motion with time period \(T\) and maximum speed \(v\). The speed of the block is measured at a random time. What is the probability that the measured speed is more than \(\frac v2?\)

---

Let's plot the block's position (light gray) and velocity (gray).

As we are interested in relative values, the specific vertical scaling of the plot is not important. Green time intervals represent times at which we would do a positive measure, where the measured speed, or absolute value of velocity, would exceed \(\frac v2\). These intervals are \(\left(k \pi + \frac{\pi}6, k \pi + 5 \cdot \frac{\pi}6\right)\) for any whole number \(k\), since the start of the first green interval from the vertical axis is at time \(t\) for which \(-\sin{t} = -\frac12\), so \(t = \frac{\pi}6\). Since the motion is periodic and the measure can take place at any time with equal probability, we can argue that the probability of a positive measure is

\[\frac{N \times 2 \left(5\cdot \frac{\pi}6 -\frac{\pi}6\right)}{N \times 2\pi} = \frac{2}{3},\]

where the system makes \(N\) periods. \(_\square\)

Johannes Kepler worked out that all planets revolve around the sun in elliptical orbits with the sun at one focus. He also deduced that planets revolve around the sun with constant areal velocity.

Let's model a small star system in which a planet revolves around the star in an elliptical orbit. It has semi-major axis \(a\) and semi-minor axis \(b\). During one revolution, the minimum speed of the planet is \(u\) and the maximum speed is \(v\). In a complete revolution, an instant of time is randomly and uniformly chosen. What is the probability that the distance between the planet and the star at that instant is more than \(b?\)

---

Kepler observed that planets don't orbit the sun at a uniform speed, but rather move faster when they are closer to the sun and more slowly when they are farther away. He specifically determined that the orbital speed of a planet is such that the line drawn from the sun to the planet sweeps out equal areas in equal intervals of time. This means that the time the planet spends at distant positions is proportional to the area the line sweeps at those positions. Our probability is then

\[ \mathbb{P}\big[(\text{measured distance}) > b\big] = \frac{(\text{time spent at distance}) > b}{(\text{time period})} = \frac{A}{A_0} = \frac{A}{\pi \, a \, b}, \]

where \(A_0\) is the area of the ellipse and \(A\) is the unknown area that the sun-planet radius vector sweeps out while the planet is far away. The problem then reduces to finding this area:

Let's draw the orbit in Cartesian coordinates with \(x\) and \(y\) in units of semi-axis \(a\). Let axis ratio \(\mu =\frac ba\), with \(\mu = 0.6\) in the picture above. The sun is at the left focus \(S\) with coordinates \(\big(-\sqrt{a^2 - b^2}, 0\big).\) Draw a circle with radius \(b\) that is centered at the sun, and find an intersection with the ellipse at point \(P\) with coordinates \(\left( -a \, \sqrt{\frac{a - b}{a + b}}, \sqrt{\frac{2 \, b^3}{a + b}} \right).\) This follows by writing down the equations of the ellipse and circle, respectively:

\[\begin{align} \left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 &= 1 \\ (x + c)^2 + y^2 &= b^2 \end{align} \]

with \(c = \sqrt{a^2 - b^2}\), and by finding point \(P\) at which the curves meet. We will naturally divide the calculation of the area by integrating the upper branch of the ellipse from the \(x\)-coordinate of \(P\), and by adding the area of triangle \(P S Q\). The picture indicates area division by different shades of green:

\[ \begin{align} A &= 2 \times \Bigg( \frac{1}{2} \cdot \left(c - a \, \sqrt{\frac{a - b}{a + b}}\right) \cdot \sqrt{\frac{2 \, b^3}{a + b}} + b \, \int_{x_1}^{x_2} \sqrt{1 - \left(\frac{x}{a}\right)^2} \, dx \Bigg)\\ &= \frac{1}{2} + \frac{1}{\pi} \cdot \left( \sqrt{2 \, \mu \, (1 - \mu)} + \arcsin{\sqrt{\frac{1 - \mu}{1 + \mu}}} \right). \end{align} \]

We integrated from \( x_1 = -a \, \sqrt{\frac{a - b}{a + b}} \) to \( x_2 = a \). Below is the plot of the resulting probability in terms of axis ratio \(\mu\). With \(\mu = 0.6\) the probability of finding the planet farther than \(b\) is about 89%. \(_\square\)

With the eccentricity of the orbit close to zero, the ellipse is heavily prolonged and the chance of finding the planet in the vicinity of the sun is small, because i) the major part of the orbit is farther from sun, and ii) when the planet does approach the sun, its speed is large, and hence its visitation time is short. On the other hand, when the eccentricity is close to one, the ellipse is close to a circle and the orbital velocity of the planet is approximately constant, which means that the planet spends about half the time at distances less than \(b\), and half the time farther away. This can be seen in the animation below where the axis ratio \( \mu \) oscillates between \(0.2\) and \(0.99\).

Caveat: Imagine the ideal case \( b = a \) of a perfect circle. If a planet orbits its sun at a constant distance \( b,\) we surely could never measure its distance at more than \( b \). But the result above suggests the chance should be even. How would you explain this?

There are many great problems in geometric probability. If you'd like some extra challenges, check out these problems. If you'd like to contribute to this wiki, you can add a solution to one of the examples!

Two numbers are chosen randomly and uniformly from \([-a, a]\). What is the probability that the absolute value of the smaller number is greater than two times the absolute value of the larger number? Does the final answer depend on the value of \(a?\)

---

Let \(X\) and \(Y\) represent the two random numbers. Chances of \(X\) being smaller than \(Y\) are even, so we can focus on the case \(X < Y\). Our probability is then

\[ \mathbb{P} \big( |X| > 2 \cdot |Y| \big) = \frac{a^2}{2} : \frac{(2 a)^2}{2} = \frac{1}{4}. \]

The probability expression involves two absolute values, so it splits to four cases, depending on the signs of the variates:

• i) \( (X < 0) \land (Y > 0)\)
• ii) \( (X < 0) \land (Y < 0)\)
• iii) \( (X > 0) \land (Y > 0)\)
• iv) \( (X > 0) \land (Y < 0)\).

Solutions of the last two, together with the starting assumption, are empty sets. The union of the solutions of the first two cases is shaded in the picture below. Mind that we divided by half of the area of the square \(2 \cdot a^2\), since we started by reducing the probability space to the region above the line \(X = Y\). Note also that the answer doesn't involve \(a\), so that it would stay the same as long as we picked the two variates from some common interval. \(_\square\)

Two points are randomly and uniformly selected on the circumference of a circle. The center of the circle and the two points are joined together. What is the probability that we obtain each of the following?

\(\begin{array}{rrl} &\text{i)} &\text{a line segment} \\
&\text{ii)} &\text{an acute-angled triangle} \\ &\text{iii)} &\text{a right-angled triangle} \\ &\text{iv)} &\text{an obtuse-angled triangle} \end{array}\)

---

We may suppose that the two points \(A\) and \(B\) are selected independently so we can, without loss of generality, select and place \(B\) relatively to \(A\).

i) Answer: \(0\). Why? Line segment would occur if \(B\) was placed at exact angle \(\pi\) to \(A\). But a continuous variable has zero chance of taking a specific value (what is the width of a point?).

ii) Answer: \(\frac{1}{2}\). Why? Triangle would be acute if \(B\) was placed at some angle in the interval \(\big[-\frac{\pi}{2}, \frac{\pi}{2}\big]\). Values \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\) (such triangle would be right-angled) and \(0\) (degenerate) should be excluded, yet again, some specific discrete values don't change the probability.

iii) Answer: \(0\). Why? See above.

iv) Answer: \(\frac{1}{2}\). Why? Triangle can be either acute or obtuse, with even chances. \(_\square\)

Two points are randomly and uniformly selected from the interior of a circle. The center of the circle and the two points are joined together. What is the probability that we obtain each of the following?

\(\begin{array}{rrl} &\text{i)} &\text{a line segment} \\
&\text{ii)} &\text{an acute-angled triangle} \\ &\text{iii)} &\text{a right-angled triangle} \\ &\text{iv)} &\text{an obtuse-angled triangle} \end{array}\)