Conic Sections
A conic section is a curve on a plane that is defined by a \(2^\text{nd}\)-degree polynomial equation in two variables. Conic sections are classified into four groups: parabolas, circles, ellipses, and hyperbolas. Conic sections received their name because they can each be represented by a cross section of a plane cutting through a cone.

\[\begin{array}{ccc}\qquad \quad\text{1: Parabola} \qquad \quad \quad & \text{2: Ellipse and Circle} & \quad \quad \quad \text{3: Hyperbola}\end{array}\]
The practical applications of conic sections are numerous and varied. They are used in physics, orbital mechanics, and optics, among others. In addition to this, each conic section is a locus of points, a set of points that satisfies a condition. Their status as loci of points allows them to be used in practical problems in which the location of an object can vary, but it needs to meet certain conditions. Understanding the coordinate geometry of conic sections allows one to model these situations with the equations of conic sections.
Contents
Cartesian Equations
Each conic section can be defined as a locus of points. A locus of points is a set of points, each location of which is satisfied by some condition. These definitions are important because they inform how to use conic sections in real-world problems.
The following sections are meant to be references. Feel free to check the linked main articles for more in-depth examples and problems.
Parabola
Main Article: Equation of a Parabola
A parabola is defined in terms of a line, called the directrix, and a point not on the directrix, called the focus. A parabola is the locus of points that are equidistant from both the directrix and focus.
The axis of symmetry is the line which divides the parabola symmetrically. The vertex of the parabola is the intersection of the axis of symmetry and the parabola.
A parabola which opens vertically has the equation
\[(x-h)^2=4p(y-k).\]

\((h,k)\) are the the coordinates of the vertex. The directrix is defined by the equation \(y=k-p\). The focus has coordinates \((h,k+p)\).
A parabola which opens horizontally has the equation
\[(y-k)^2=4p(x-h).\]
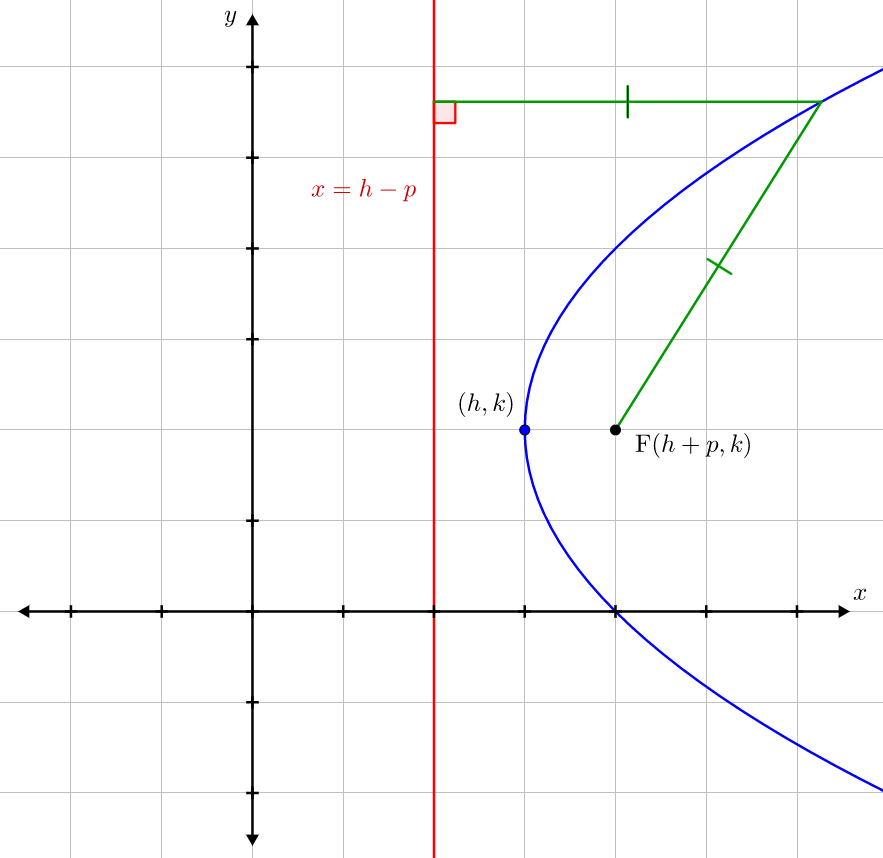
\((h,k)\) are the coordinates of the vertex. The directrix is defined by the equation \(x=h-p\). The focus has coordinates \((h+p,k)\).
Circle
Main Article: Equation of a Circle
A circle is defined in terms of a point, called the center, and a non-zero length, called the radius. A circle is the locus of points located a radius away from the center:
\[(x-h)^2+(y-k)^2=r^2.\]

\((h,k)\) are the coordinates of the center of the circle and \(r\) is the radius of the circle.
Ellipse
Main Article: Equation of an Ellipse
An ellipse is defined in terms of two points, called foci (plural of focus). An ellipse is the locus of points for which the sum of the distances to each of the foci is a constant amount. This constant amount is equal to the length of the major axis:
\[\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1.\]

\((h,k)\) are the coordinates of the center of the ellipse. The center is the midpoint of the two foci. The chord which passes through the two foci is called the major axis. The chord that is perpendicular to the major axis and passes through the center is called the minor axis.
If \(a>b\), then the ellipse will have a horizontal major axis of length \(2a\) and a vertical minor axis of length \(2b\). The foci will be located at \(\left(h-\sqrt{a^2-b^2},k\right)\) and \(\left(h+\sqrt{a^2-b^2},k\right)\).

If \(a<b\), then the ellipse will have a vertical major axis of length \(2b\) and a horizontal minor axis of length \(2a\). The foci will be located at \(\left(h,k-\sqrt{b^2-a^2}\right)\) and \(\left(h,k+\sqrt{b^2-a^2}\right)\).

If \(a=b\), then the ellipse is a circle. A circle is sometimes considered to be a sub-type of ellipses in which the two foci coincide with one another.
Hyperbola
Main Article: Equation of a Hyperbola
A hyperbola is defined in terms of two points, called foci. A hyperbola is the locus of points for which the absolute difference of the distances to each of the foci is a constant amount. This constant amount is equal to the distance between the vertices of the hyperbola. The foci are located on a line called the transverse axis. The midpoint of the two foci is the center.
The standard form equation of a hyperbola with a horizontal transverse axis is
\[\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1.\]

The vertices are located at \((h-a,k)\) and \((h+a,k)\). The foci are located at \(\left(h-\sqrt{a^2+b^2},k\right)\) and \(\left(h+\sqrt{a^2+b^2},k\right)\).
The standard form equation of a hyperbola with a vertical transverse axis is
\[\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1.\]

The vertices are located at \((h,k-a)\) and \((h,k+a)\). The foci are located at \(\left(h,k-\sqrt{a^2+b^2}\right)\) and \(\left(h,k+\sqrt{a^2+b^2}\right)\).
In either case, \((h,k)\) are the coordinates of the center of the hyperbola. One can draw a rectangle centered around this point with side lengths \(2a\) and \(2b\). The lines containing the diagonals of this rectangle are the asymptotes of the hyperbola.

Brent is planning his running route. He would like the route to meet the following conditions:
- He will start at his house, located at \((0,0)\).
- He will travel in a straight line to some point, \(\text{A}\).
- He will then travel in a straight line to the school, located at \((8,0)\) (8 km east of his house).
- Finally, he will travel in a straight line back to his house.
- He would like the entire route to be exactly 18 km (a distance of 18 units in the coordinate plane).
Which of these is an equation of the locus of points that Brent could select as point \(\text{A}\) in his running route?
Let the equation of an ellipse be \[\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1.\] Now, a point \(P=(\alpha ,\beta )\) lies on the ellipse and a tangent is drawn to the ellipse at that point.
The perpendicular distance from the origin to this tangent is 5, and the perpendicular distances from the foci to the tangent are \(P_1\) and \(P_2\), respectively.
If \(b=3,\) what is the absolute value of \((P_1-P_2) ?\)
Applications
The math of conic sections comes up often in the study of physics. The math of circles is applicable in uniform circular motion. Parabolas are applicable in kinematics problems. An object that is moving laterally with constant velocity, subject to gravity, will trace a parabolic path. For example, a ball thrown from a building follows a parabolic path. The parametric equations given at the bottom of this page are especially applicable for physics.
Kepler's laws describe the motion of objects in space. One of the laws describes the shape of a planet around the sun as an ellipse with the sun as a focus. Objects that are not bound in orbit travel in a parabolic or hyperbolic path relative to each other.
Parabolas are used in optics. A parabola is a two-dimensional, mirror-symmetrical curve, which is approximately U-shaped when oriented as shown in the diagram below but can be in any orientation in its plane.

It fits any of several superficially different mathematical descriptions which can all be proved to define curves of exactly the same shape. A mirror that has a cross-sectional parabolic shape has the property that all light shone directly towards it will be reflected towards the focus of the parabola. A parabolic reflector is a mirror or reflective device that uses this property to concentrate reflected light onto a single point. These kinds of mirrors are used in microwave and satellite technology.
General Form of Conic
All conic sections can be described by \(2^\text{nd}\)-degree polynomials in two variables. The general form equation of a conic section is given below:
General Equation of a Conic Section:
\[Ax^2+Bxy+Cy^2+Dx+Ey+F=0\]
If the \(B\) coefficient is zero, then the conic section is oriented horizontally or vertically. The equation can be put into one of the specific forms above by completing the square.
An equation of a conic section is given below. Put the equation into one of the standard forms:
\[25x^2-4y^2-100x-24y-36=0.\]
Rearrange and group the terms in the equation:
\[(25x^2-100x)-(4y^2+24y)=36.\]
Factor each grouping:
\[25(x^2-4x)-4(y^2+6y)=36\]
Add or subtract constants from each side of the equation to complete the perfect square trinomials:
\[\begin{align} {\color{red}25}(x^2-4x+{\color{red}4}){\color{blue}-4}(y^2+6y+{\color{blue}9})&=36{\color{red}+25\cdot 4}{\color{blue}-4\cdot 9}\\ 25(x^2-4x+4)-4(y^2+6y+9)&=100. \end{align}\]
Factor the perfect square trinomials:
\[25(x-2)^2-4(y+3)^2=100.\]
Divide both sides by the constant on the right hand side of the equation:
\[\frac{(x-2)^2}{2^2}-\frac{(y+3)^2}{5^2}=1.\]
By completing the square, it can be observed that the original equation was a hyperbola centered at \((2,-3)\). \(_\square\)
If the \(B\) coefficient is not zero in the general form equation, then the conic section is oriented on a slant axis.

\[\text{Graph of }x^2+2 x y+y^2-4 x-2 y-3=0\]
The type of conic section that the equation is describing can be determined by calculating the discriminant of the conic section. Below is a short example, but there are many more examples in the linked page.
Determine what kind of conic section the equation below describes:
\[x^2+2 x y+y^2-4 x-2 y-3=0.\]
We have
\[\begin{array} &A=1, &B=2, &C=1, &D=-4, &E=-2, &F=-3.\end{array}\]
Then
\[\begin{array}&a=B=1, &b=C=1, & c=F=-3, &f=\frac{1}{2}E=-1, &g=\frac{1}{2}D=-2, &h=\frac{1}{2}B=1.\end{array}\]
Therefore, \[\begin{align} \Delta &= \begin{vmatrix} a & h & g \\ h & b & f \\ g & f & c \end{vmatrix}\\ &=abc+2fgh-a{ f }^{ 2 }-b{ g }^{ 2 }-c{ h }^{ 2 } \\ &=-1, \end{align}\]
which is non-zero, so the equation is non-degenerate. The nature of the conic is given by
\[B^2-4AC=0.\]
Because this discriminant is zero, the conic section is a parabola. \(_\square\)
Polar Equations
The equations for each conic section can be converted to polar form. For vertically or horizontally oriented conic sections with a focus at the origin, a rather simple conversion is available using the eccentricity and semi-latus rectum of the conic section.
Let \(d_1\) be the length of a segment connecting a point on the conic section to a focus. Let \(d_2\) be the length of a segment, perpedicular to the directrix, that connects the same point to the directrix. The ratio of these two segment lengths, called the eccentricity of the conic section, is always a constant amount: \(e=\frac{d_1}{d_2}.\)

A circle has \(e=0\). The circle is the only conic section that does not have a directrix.
An ellipse has \(0<e<1\).
A parabola has \(e=1\).
A hyperbola has \(e>1\).

The latus rectum is the chord parallel to the directrix which passes through the focus.
A semi-latus rectum, each labeled as \(l\) in the picture below, is half of the latus rectum that passes from the focus to the conic section.

Although the picture above demonstrates a parabola's latus rectum, each conic section has latus rectum(s). The latus rectum of a circle is simply the diameter of the circle.
Polar Form of a Conic Section:
Given a horizontally or vertically oriented conic section with a focus at the origin, the polar form equation is
\[r=\frac{l}{1+e\cos{\theta}},\]
where \(e\) is the eccentricity of the conic section, and \(l\) is the length of the semi-latus rectum.
A table containing the values of the eccentricity and the length of the semi-latus rectum for each conic section is given below. The values of \(a\) and \(b\) correspond to the values in the Cartesian equations above.
Values of Eccentricity and Length of Semi-Latus Rectum:
Let \(e\) be the eccentricity of the conic section, and let \(l\) be the length of the semi-latus rectum.
\[\begin{array}{|c|c|c|} \hline \text{Conic Section} & e & l \\ \hline \text{Circle} & 0 & r \\ \hline \quad \text{Ellipse with }a>b\quad &\quad \sqrt{1-\frac{b^2}{a^2}\quad } &\quad \frac{b^2}{a}\quad \\ \hline \text{Ellipse with }b>a & \sqrt{1-\frac{a^2}{b^2}} & \frac{a^2}{b} \\ \hline \text{Parabola} & 1 & 2p \\ \hline \text{Hyperbola*} & \sqrt{1+\frac{b^2}{a^2}} & \frac{b^2}{a} \\ \hline \end{array}\]
(*) In this convention, a hyperbola with a horizontal transverse axis has equation \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), and a hyperbola with a vertical transverse axis has equation \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\).
Write an equation in polar form for an ellipse that has semi-major axis \(13\) and semi-minor axis \(5\).
Let \(a=13\) and \(b=5\). Using the table above,
\[\begin{align} e &= \sqrt{1-\frac{b^2}{a^2}} =\frac{12}{13} \\ \\ \\ l &= \frac{b^2}{a} =\frac{25}{13}. \end{align}\]
Then the equation of the ellipse in polar form is
\[\begin{align} r &= \frac{l}{1+e\cos{\theta}} \\ \\ &=\frac{25}{13+12\cos{\theta}}. \ _\square \end{align}\]
Parametric Equations
Each standard Cartesian equation can be converted to parametric equations. Each set of parametric equations is given below, and they correspond to the equations above.
Parametric Equations for Conic Sections:
\[\begin{array}{|c|c|c|} \hline \text{Conic Section} & x & y \\ \hline \text{Circle} & r\cos{t}+h & r\sin{t}+k \\ \hline \text{Ellipse} & a\cos{t}+h & b\sin{t}+k \\ \hline \text{Vertical Parabola} & 2pt+h & pt^2+k \\ \hline \text{Horizontal Parabola} & pt^2+h & 2pt+k \\ \hline \quad \text{Horizontal Hyperbola*}\quad &\quad a\sec{t}+h\quad &\quad b\tan{t}+k\quad \\ \hline \text{Vertical Hyperbola*} & b\tan{t}+h & a\sec{t}+k \\ \hline \end{array}\]
(*) In this convention, a hyperbola with a horizontal transverse axis has equation \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), and a hyperbola with a vertical transverse axis has equation \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\).
Convert the following equation to parametric equations:
\[(y+4)^2=-12(x-1).\]
The equation is a horizontal parabola. The following values can be taken from the equation:
\[p=-3, \quad h=1, \quad k=-4.\]
Using the table above, the parametric equations are
\[\begin{array}{ll} x&=pt^2+h &&& y&=2pt+k \\ &=-3t^2+1 &&& &=-6t-4. \ _\square \end{array}\]