Introduction to Kinematics
The most fundamental quantities in kinematics are position and velocity. They track an object's motion through space at any given time, in terms of both the current and future locations of the object.
These fundamental concepts of physics are derived using calculus, although a first presentation of the equations of motion usually avoids the use of calculus. To understand kinematics, therefore, one must understand derivatives and rates of change as well as integrals.
Position
Position
The position of an object is any way to unambiguously establish its location in space, relative to a point of reference. This can be accomplished using a coordinate system, such as a Cartesian grid, a spherical coordinate system, or any other generalized set of coordinates.
In short, the position of an object is just its location in some coordinate system. One can consider the position-time graph or displacement-time graph of an object, in which the \(x\)-axis represents the time and the \(y\)-axis represents the displacement. Such a graph shows how the position evolves as a function of time, \(x(t)\).
Displacement is a slightly distinct concept from distance or position. Unlike distance, displacement is a vector quantity. It gives the net change in position from a fixed initial position, as opposed to the total distance traveled. For example, if an object is at \(x_1\) at time \(t_1\), and it is at \(x_2\) at time \(t_2\), then the displacement will be
\[d=x_2-x_1=x(t_1+\Delta t)-x(t_1),\]
where \(\Delta t = t_2-t_1\).
Note that the "rate of change of \(y\) with respect to \(x\)" refers to the derivative of \(y\) with respect to \(x\), \(\frac{dy}{dx}\), or the slope of the function \(y\) at a given point.
You start at point \(A\) and travel \(4\text{ km}\) to the south and then \(3\text{ km}\) to the east, finally reaching \(C.\) Find the total distance and displacement traveled by you.
You should always remember that distance traveled is the actual path taken and displacement is the shortest path possible. The question can be visualized in a diagram as shown:

Distance traveled is \(AB + BC = 4 + 3 = 7~\text{km}.\)
Displacement, being the shortest path, is the length of \(AC\). Applying Pythagorean theorem to \(\triangle ABC,\) we get \(AC = \sqrt{AB^2 + BC^2} = \sqrt{4^2+ 3^2} = 5~\text{km}.\)
Note that you can find displacement using vectors. The displacement vector \(\vec{AC} = \vec{AB} + \vec{BC} = -4\overline{i} + 3\overline{j}\) and \(|\vec{AC}| = \sqrt{4^2 + 3^2} = 5\).
Velocity
Velocity
The velocity of an object is the rate at which an object changes its position. The direction of an object's velocity at any time is parallel to the tangent vector of the curve representing the trajectory of the object.
From the definition, the derivative of the position function yields the velocity function:
\[v(t)=\dfrac{dx}{dt}=\displaystyle\lim_{\Delta t\rightarrow 0}\dfrac{x(t+\Delta t)-x(t)}{\Delta t} =\displaystyle\lim_{\Delta t\rightarrow 0}\dfrac{x_2-x_1}{\Delta t}. \]
Often, the term speed is used instead of velocity. The speed of an object is the norm of the velocity, i.e. it gives the magnitude but not the direction of the velocity.
The speed function is, therefore,
\[|v(t)|=\left|\dfrac{dx}{dt}\right|=\left|\displaystyle\lim_{\Delta t\rightarrow 0}\dfrac{x(t+\Delta t)-x(t)}{\Delta t}\right|.\]
Since the velocity of a particle is the derivative of its position, we can go the other way around to get displacement by integrating the velocity function; that is,
\[\int v(t) = \int \frac{ds}{dt}=s(t) + C,\]
where \(C\) is an arbitrary constant which can be found out if we are given an initial value.
The displacement of an object at some given time \(t\) is given by the function \(x(t)=3t^2-2t-1\). Find the function that gives its velocity at all times and evaluate for \(t=3\) and \(t=5\).
Since the velocity is the derivative of the displacement function,
\[v(t)=\dfrac{d}{dt}\big(3t^2-2t-1\big)=6t-2.\]
Therefore, the speed function will be \(\big|v(t)\big|=|6t-2|\). As a result, the velocity and speed at \(t=3\) are
\[\begin{align} v(3)=6(3)-2&=16 \text{ m/s} \\ \big|v(3)\big|=|16|&=16\text{ m/s}, \end{align}\]
and at \(t=5\)
\[\begin{align} v(5)=6(5)-2&=28\text{ m/s}\\ \big|v(5)\big|=|28|&=28\text{ m/s}.\ _\square \end{align}\]
Astronauts on an atmosphere-less planet wanted to find the acceleration due to gravity. In order to find it, they launched a ball from the surface of the planet, with a velocity of \(15\text{ m/s},\) and predicted that the ball would reach a height of \[s=15t-\dfrac 12 g_pt^2\] meters \(t\) seconds after the launch. If the ball reached the maximum height after \(20\) seconds, what was the value of \(g_p?\)
Try my set Gravity if you'd like to solve more such problems!
Acceleration
Acceleration
The acceleration of an object is given by the rate of change of the object's velocity. If an object moves with constant velocity, then its acceleration is zero. If an object changes its speed or the direction of its velocity, then it has a non-zero acceleration.
Since acceleration is the rate of change of velocity, it is the derivative of the velocity function:
\[a(t)=\dfrac{dv}{dt}=\dfrac{d^2x}{dt^2}.\]
Similarly, we can deduce the velocity and displacement functions by integrating the acceleration function once and twice respectively:
\[\begin{align} \int a(t) &=\int \frac{dv}{dt}\\ &=v(t)+C\\\\ \iint a(t) &= \iint\frac{d^2s}{dt^2}\\ &=s(t)+C, \end{align}\]
where \(C\) is an arbitrary constant.
A ball falls freely at \(t=0\) and the displacement is given by the function \(x(t)=-\frac12 gt^2\). Find its velocity, speed, and acceleration at \(t=2\). Take \(g=9.8 \text{ m}/\text{s}^2\).
Since the velocity is the derivative of the displacement function,
\[v(t) = \dfrac{dx}{dt} =\dfrac{d}{dt}\left(-\dfrac12 gt^2\right)= -gt.\]
Therefore, \(v(2)= -9.8(2)=-19.6 \text{ m/s}.\)
The speed is the absolute value of \(v(t)\), so \[\text{speed}=\big|v(t)\big|=19.6 \text{ m}/\text{s}.\]
Finally, the acceleration is the derivative of the velocity function, so
\[a(t)= \dfrac{dv}{dt} =\dfrac{d}{dt}(-gt)=-g,\]
and one computes that \(a(2)=-9.8\text{ m}/\text{s}^2\). \(_\square\)
Velocity vs. Acceleration
It is important to recognize that the acceleration of an object only gives the rate of change of the velocity and is not correlated with the speed of an object. It is possible for an object to move very slowly, quickly, or not move at all, and have any variety of magnitudes of acceleration.
Graphically, the acceleration represents the slope of the tangent to the velocity-time plot. The velocity could be very large and negative, with a very large and positive slope. In this case, the object would be moving quickly backward but slowing down and reversing direction in a short amount of time.
A common misconception is that an acceleration always represents a change in speed. This is not correct. Because acceleration is a vector quantity, changes in the direction of velocities also constitute accelerations. Therefore, an object moving in a circle at constant speed is also constantly accelerating because the direction of the velocity vector is rotating at every instant in time.
The below plot gives two curves representing velocity as a function of time for two different particles.
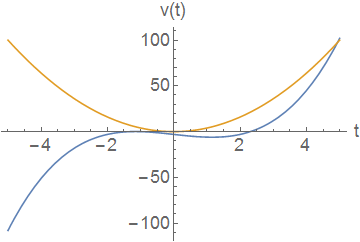 Two curves giving velocity as a function of time of two particles
Two curves giving velocity as a function of time of two particles
For which curve is the magnitude of the acceleration greater at \(t=0?\)
The below plot gives two curves representing velocity as a function of time for two different particles.
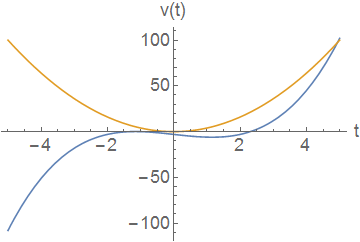 Two curves giving velocity as a function of time of two particles
Two curves giving velocity as a function of time of two particles
For which curve is the magnitude of the velocity greater at \(t=0?\)
A small toy car (car A) is kicked so that it travels at \(2 \text{ m}/\text{s}\) to the right without friction. Simultaneously, another toy car (car B) accelerates from rest via an electric motor at \(0.9 \text{ m}/\text{s}^2\) to the right without friction. Which reaches the finish line \(10 \text{ m}\) away first?