Converting Degrees and Radians
Contents
Measuring Angles
There are two different systems for measuring angles: degrees and radians. To measure in degrees, we first consider a full revolution as \(360^\circ\). Then by evenly dividing the revolution into 360 parts, each of these parts is \(1^\circ\) and for any integer \(1 \leq d \leq 360,\) the measure of \(d\) combined parts gives \(d^\circ.\) The value 360 satisfies the nice property that it has many divisors \( (2, 3, 4, 5, 6, 8, 10, 12, 15, \ldots). \)
The second system of measurement is by radians, in which we measure an angle by measuring the arc length of the unit circle. Consider a unit circle centered at the origin and let \(\theta\) denote an angle formed with the positive \(x\)-axis.
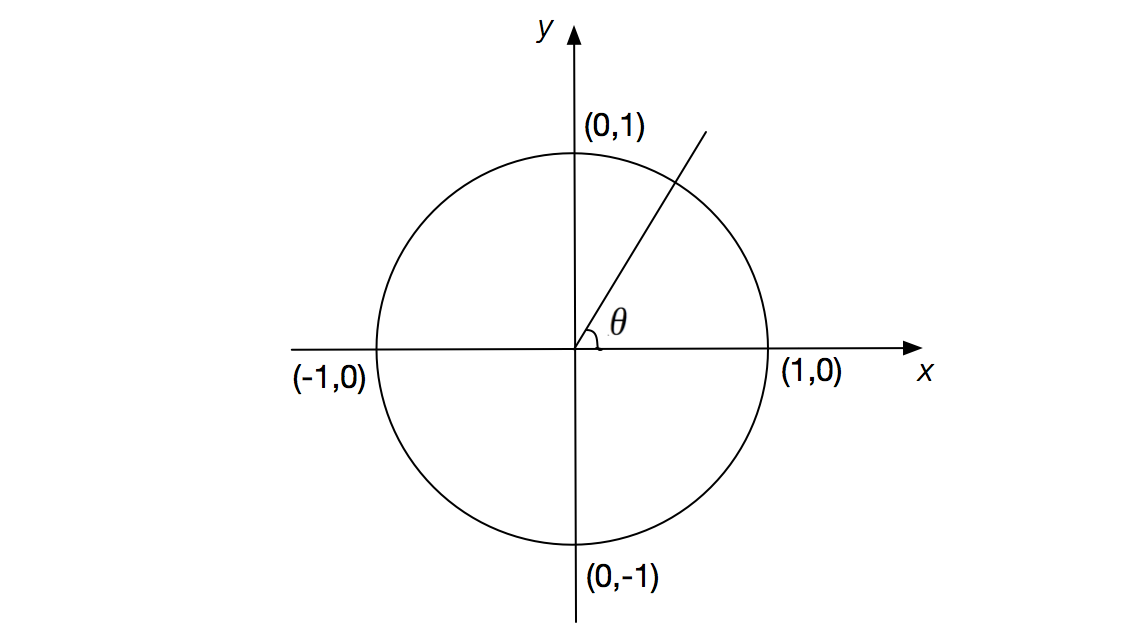
Then the measure of angle \(\theta\) in radians is the arc length of the circle carved out by the angle. To see how to compute this, let's start with a few easy examples. If the angle measures \(0^\circ\) in degrees, then the arc length of the circle carved out by the angle is \(0\). On the other hand, if the angle measures \(360^\circ\) in degrees, then the arc length of the circle carved out by the angle is the circumference of a circle with radius \(1\), or \(2 \pi \cdot 1 = 2\pi.\) For any other angle measurement in degrees, we can calculate the fraction of the arc length carved out by converting from degrees to radians, as shown in the following example:
What is the measure of a right angle in radians?
Since a right angle is \(90^\circ\) in degrees, we have
\[ 90^\circ = 90^\circ \times \frac{\pi \text{ radians} }{180^\circ} = \frac{\pi }{2} \text{ radians}. \ _\square\]
Converting between degrees and radians:
- To convert a measure in degrees to radians, multiply by \(\frac{\pi \text{ radians}}{180^\circ}\).
- To convert a measure in radians to degrees, multiply by \(\frac{180^\circ}{\pi \text{ radians}}\).
Another simple way to convert the degrees into radians is to use the following formula: \[\frac{D}{90}=\frac{\ \ R\ \,}{\frac{\pi}{2}}.\] This is true because the numbers of radians in \(90^\circ\) is equal to \(\dfrac{\pi}{2}\) radians. So, we can equate the expressions and derive this expression.
Here are a few radian measures that are useful to know:
\[\begin{array} &30^\circ = \frac{\pi }{6} \text{ radians}, &60^\circ = \frac{\pi }{3} \text{ radians}, &90^\circ = \frac{\pi }{2} \text{ radians}, &180^\circ = \pi \text{ radians}. \end{array}\]
Arc Lengths
For a general circle with radius \(r\), if an angle \(\theta\) (given in radians) is formed with the positive \(x\)-axis, then the arc length of the portion of the circle carved out by the angle is
\[ \text{(Arc Length)} = r \theta. \]
As we have seen, for a circle with radius \(r=1,\) the arc length is simply the angle \(\theta\) in radians.
Examples
Convert the following from radians to degrees:\[\]
\[ \pi \text{ radians}, ~ \frac{\pi}{2} \text{ radians}.\]
Since \( 1 \text{ radian} = \frac{360^\circ}{2\pi} ,\) we have
\[ \begin{align} \pi \text{ radians} &= \pi \text{ radians} \cdot \frac{360^{\circ}}{2\pi \text{ radians}} \\ &= 180^\circ. \end{align} \]
Similarly,
\[ \begin{align} \frac{\pi}{2} \text{ radians} &= \frac{\pi}{2} \text{ radians} \cdot \frac{360^{\circ}}{2\pi \text{ radians}} \\ &= 90^\circ. \ _\square \end{align} \]
Convert the following from degrees to radians:\[\]
\[60^\circ, ~180^\circ. \]
Since \( 2 \pi \text{ radians} = \frac{360^\circ}{2\pi} ,\) we have
\[\begin{align} 60^\circ &= 60^\circ \cdot \frac{2 \pi \text{ radians}}{360^\circ} \\ &= \frac{\pi}{3} \text{ radians} \\ \\ 180^\circ &= 180 \cdot \frac{2 \pi \text{ radians}}{360^\circ} \\ &= \pi \text{ radians}. \ _\square \end{align} \]
What is the central angle \(\theta\) (in radians) that subtends an arc of length 4 and radius 2?
Approach 1:
When an arc length equals its radius, then the central angle that subtends the arc is 1 radian.
Since the arc length of the circle is twice the radius in this problem, the central angle is 2 radians. \(_\square\)Approach 2:
The length \(l\) of an arc of radius \(r\) and central angle \(\theta\) is given by the formula \[l=r\theta.\] For this problem we have \[ \begin{align} l &= r\theta \\ 4 &= 2\theta \\ \theta &= 2 \text{ radians}.\ _ \square
\end{align} \]