Unit Circle

Contribute to this wiki by adding relevant examples! For more information, see here.

The unit circle is a circle of radius 1 unit that is centered on the origin of the coordinate plane.

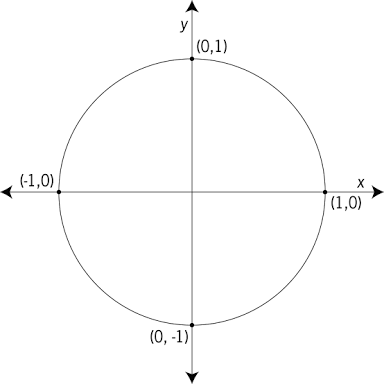
The unit circle is fundamentally related to concepts in trigonometry. The trigonometric functions can be defined in terms of the unit circle, and in doing so, the domain of these functions is extended to all real numbers.

The unit circle is also related to complex numbers. A unit circle can be graphed in the complex plane, and all roots of unity will lie on this circle.

Every point on the unit circle corresponds to a right triangle with vertices at the origin and the point on the unit circle. The right triangle has leg lengths that are equal to the absolute values of the \(x\) and \(y\) coordinates, respectively.

This right triangle is used to apply trigonometric relations.

\[ \begin{array}{rll} \sin (\theta) & = \frac{\text{opposite}}{\text{hypotenuse}} & = \frac{b}{c} \\ \\ \cos (\theta) & = \frac{\text{adjacent}}{\text{hypotenuse}} & = \frac{a}{c} \\ \\ \tan (\theta) & = \frac{\text{opposite}}{\text{adjacent}} & = \frac{b}{a} \\ \\ \end{array}\]

Since the hypotenuse of the right triangle is always 1 unit long, the values of the \(x\) and \(y\) coordinates of a point on the circle are always equal to the cosine and sine (respectively) of the angle \(\theta.\)

This angle is measured in a unit called radians, which corresponds to the distance around the unit circle from the point \((1,0).\) The circumference of the unit circle is \(2\pi,\) so \(2\pi\) radians is the same as 360\(^\circ.\) Any other angle less than 360\(^\circ\) can be represented as some fraction of \(2\pi\) radians. For example, A 90\(^\circ\) angle is the same as \(\frac{1}{4}\) of the way around the circle, which would be \(\frac{2\pi}{4}=\frac{\pi}{2}.\)

Some possible values of \(\theta\) are listed below, along with their corresponding values of sine and cosine.

\[ \begin{array} { | c | c | c | } \hline \text{angle measure, } \theta & \sin \theta & \cos \theta\\ \hline 0 & 0 & 1 \\ \hline \dfrac{\pi}{6} & \dfrac{1}{2} & \dfrac{\sqrt{3}}{2} \\ \hline \dfrac{\pi}{4} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \\ \hline \dfrac{\pi}{3} & \dfrac{\sqrt{3}}{2} & \dfrac{1}{2} \\ \hline \dfrac{\pi}{2} & 1 & 0 \\ \hline \end{array} \]

The trigonometry we are familiar with so far is based on only right triangles and acute angles. However, with help of Unit Circle we can extend our understanding of trigonometric functions plus also become familiar with the use of non-acute angles.

More information about the circular system of angle measurement can be found on its wiki page.

An angle on Unit Circle is always measured from the positive \(x\)-axis, with its vertex at the origin. It is measured to a point on the unit circle. The ray that begins at the origin and contains the point on the unit circle is called the terminal side.

An angle is said to be positive if it is measured by going in anticlockwise direction from the positive \(x\)-axis and negative if it is measured by going in clockwise direction from the \(x\)-axis.

Since \(2\pi \text{rad}=360^\circ,\) any degree measurement can be converted to radians, and vice versa.

Let \(d\) be an angle's measurement in degrees, and let \(r\) be that same angle's measurement in radians.

\[r = \frac{\pi d}{180}\]

\[d = \frac{180r}{\pi}\]

A right triangle \(AOB\) with right angle at \(A\) lies on the Cartesian plane such that \(\overline{OA}\) lies on the \(x\)-axis , point \(O\) lies on the origin and point \(B\) lies anywhere on the Unit Circle. Note that \(OB=1\) units.

The sine and cosine trigonometric functions are given below. When defining these functions in terms of the unit circle, it is possible to have negative lengths. If \(\overline{OA}\) is along the negative \(x\)-axis, then \(OA\) is considered to be negative. Likewise, if \(\overline{AB}\) extends below the \(x\)-axis, then \(AB\) is considered to be negative.

\[ \begin{align} \sin (\theta) &= \frac{\text{opposite}}{\text{hypotenuse}} = \frac{AB}{OB} = \frac{AB}{1} = AB\\ \cos (\theta) &= \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{OA}{OB} = \frac{OA}{1} = OA. \end{align}\]

By this convention, the sine of an angle is considered to be the \(y\)-coordinate of a point on the unit circle given by that angle. Likeways, the cosine of an angle is considered to be the \(x\)-coordinate of a point on the unit circle given by that angle. In general, to compute the sine or cosine of any angle \(\theta,\) look at the coordinates of the point on unit circle made by that angle.

Main Article: Special Angles on Unit Circle

The special angles are angles on the unit circle for which the coordinates are well-known. These coordinates can be solved for with right-triangle relationships.

\[\text{The sixteen special angles (measured in radians) on the unit circle, each labeled at the terminal point.}\]

Given that a line passes through the unit circle with the angle \(\theta=\dfrac{\pi}{4}\) find the x,y. Refer to the given diagram.

---

We know that \(\begin{cases} \cos(\theta)= x \\ \sin(\theta)=y\end{cases}\). put the value of theta to find\[\begin{cases} x=\dfrac{\sqrt{2}}{2}\\y=\dfrac{\sqrt{2}}{2}\end{cases}\]We are done\(_\square\)

A line passes through the unit circle at the point at \(x=\dfrac{1}{2}\). find the value of \(\tan^2(\theta)\)

---

first, we know that \(x^2=\cos^2(\theta)=\dfrac{1}{4}\). we also know \(y^2=\sin^2(\theta)=1-cos^2(\theta)=\dfrac{3}{4}\). using another trig identity we have \(\tan^2(\theta)=\dfrac{\sin^2(\theta)}{\cos^2(\theta)}=\boxed{3}\) we are done\(_\square\)