Doppler Effect

The Doppler effect causes a wave to be received with a frequency different from the one with which it is emitted as a result of the motion of the emitter and/or receiver. The effects are most commonly studied in sound waves and light waves.

It is noticeable when a train or a car passes by while emitting a horn sound. As it approaches, its horn sounds higher in pitch. However, as it leaves, the sound of the horn apparently has a lower pitch. This is because, when the observer and source approach each other, the frequency increases, but when they recede away, the frequency decreases. The true frequency (or emitted frequency) of the horn is actually somewhere between the "approach" and "recede" frequencies.

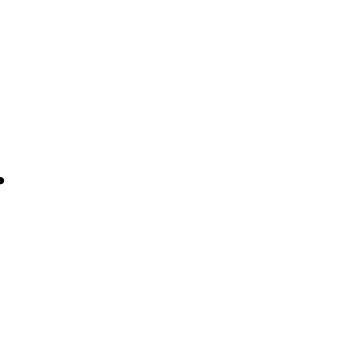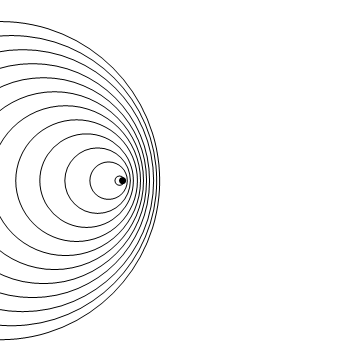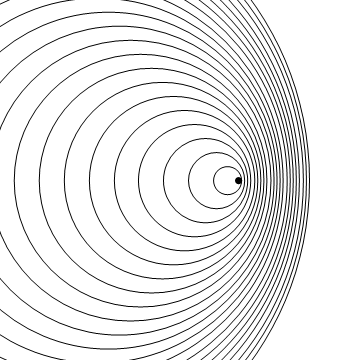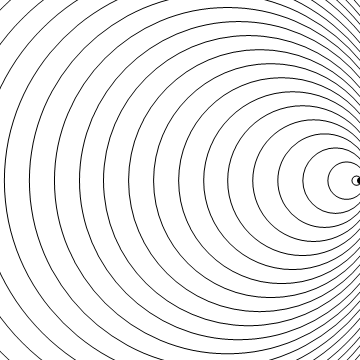The wave fronts in front of the source become close together, meaning a stationary observer on the right side of the .gif receives an effectively higher pitch. ^[1]

To see what causes this apparent frequency change, imagine a boat that is lying at anchor in a gentle sea where the waves have a time period of T = 3.0 sec. This means that every 3.0 second a crest hits the boat. The following figure shows this situation, with the water waves moving toward the left. If a watch is set to t = 0 just as one crest hits, the watch will read 3.0 sec when the next crest hits and 6.0 sec when the third crest hits, and so on.

A person in a boat with water waves moving towards him

From these observations, it can be concluded that the wave frequency is f = 1/T = 1/(3.0 s) = 0.33 Hz. Now suppose the boat is headed directly into the incoming waves. Again, the watch is set to t = 0 as a crest hits the front of the boat. Now, however, because the boat is moving towards the next wave crest as it moves toward the boat, it hits the boat in less than 3.0 s after the first hit. In other words, this period observed is shorter than the 3.0 s period observed when the boat was stationary. Because f = 1/T, a higher wave frequency is observed than when the boat was at rest.

Boat moving towards the water waves

If the boat is turned around and move in the same direction as the waves, the opposite effect is observed. The watch is set to t = 0 as a crest hits the back of the boat. Because the boat is now moving away from the next crest, more than 3.0 s will elapse on the watch by the time that crest catches the boat. Thus, a lower frequency than when you were at rest will be observed.

Boat moves in the direction of water waver and water waves hit the boat from behind

These effects occur because the relative speed between the boat and the waves depends on the direction of travel and on the speed of the boat. When the boat is moving towards the right, this relative speed is higher than that of the wave speed, which leads to the observation of an increased frequency. When the boat is turned around and move to the left, the relative speed is lower, as is the observed frequency of the water waves.

Let us now examine a situation with sound waves. In this case, an observer O is moving and a sound source S is stationary. For simplicity, we assume that the air is also stationary and that the observer moves directly toward the source. The observer moves with a speed \({v_o}\) toward a stationary point source \({v_s} = 0\), where stationary means at rest with respect to the medium, air.

If a point source emits sound waves and the medium is uniform, the waves move at the same speed in all directions radially away from the source; such wave is called as spherical wave. It is useful to represent these waves with a series of circular arcs concentric with the source, as in the figure. Each arc represents a surface over which the phase of the wave is constant. For example, the surface could pass through the crests of all waves. We call such a surface of constant phase a wavefront. The distance between adjacent wave fronts equals the wavelength \(\lambda \). In the figure, the circles are the intersections of these three-dimensional wave fronts with the two-dimensional paper.

We take the frequency of the source in figure to be \(f\), the wavelength to be \(\lambda \), and the speed of sound to be \(v\). If both the observer and the source are stationary, then he or she would detect wave fronts at rate \(f\). (That is, when \({v_o}=0\) and \({v_s} = 0\), the observed frequency is the same as the emitted frequency.)

An observer, moving towards a stationary sound source, notices an increase in frequency

When the observer moves toward the source, the speed of the waves relative to the observer is \(v' = v + {v_o}\), as in the case of the boat. What about the wavelength? Wavelength is the distance between the two consecutive crests. The observer will find the relative distance between the received crests is still \(\lambda\); only this distance is covered at a faster rate and in lesser time as the observer himself is travelling towards these crests. Thus, the wavelength \(\lambda \) remains unchanged. Hence, using an equation
\[v = f\lambda, \] we can say that the frequency \(f'\) heard by the observer is increased and is given by
\[f' = \frac{{v'}}{\lambda } = \frac{{v + {v_o}}}{\lambda }.\] Because \(v = f \lambda \), we can express \(f'\) as
\[f' = \left( {\frac{{v + {v_o}}}{v}} \right)f,\] where the observer is moving toward the source.

If the observer is moving away from the source, the speed of the wave relative to the observer decreases and \(v' = v - {v_o}\). The frequency heard by the observer in this case is decreased and is given by
\[f' = \left( {\frac{{v - {v_o}}}{v}} \right)f.\]

In general, whenever an observer moves with a speed \({v_o}\) relative to a stationary source, the frequency heard by the observer is given by \(f' = \left( {\frac{{v + {v_o}}}{v}} \right)f\) with the following sign convention: a positive value is substituted for \({v_o}\) when the observer moves toward the source, and a negative value is substituted when the observer moves away from the source.

Now consider the situation in which the source is in motion and the observer is at rest. There are two observers \(A\) and \(B\) along the same line of motion of the source, and the source moves towards \(A\) and away from \(B.\) Let the source emit a crest at \(t=0.\) This crest moves in all directions and expands radially with speed \(v\). The source is also moving with speed \({v_s}.\) After a time period \(t=T,\) the source emits another crest. At this instant in time the first crest has traveled a distance \(vT\) and the source has moved by \({v_s}T\). Thus the observer \(A\) will notice the distance between the two crests to be decreasing and observer \(B\) will notice the distance between the two crests to be increasing.

A sound source (S) moving towards a stationary observer with speed \({v_s}\)

As a result, the wavelength \(\lambda '\) measured by observer \(A\) is shorter than the wavelength \(\lambda\) of the source. The observed wavelength \(\lambda '\) is \[\lambda ' = \lambda - {v_s}T \] Also, \(T=1/f,\) implying that \[\lambda ' = \lambda - \frac{{{v_s}}}{f}.\] Because \(\lambda = v/f\), the frequency \(f'\) heard by observer \(A\) is \[\begin{align} f'&= \frac{v}{{\lambda '}} \\ &= \frac{v}{{\lambda - ({v_s}/f)}} \\ &= \frac{v}{{(v/f) - ({v_s}/f)}}\\
&= \left( {\frac{v}{{v - {v_s}}}} \right)f, \end{align}\] where the source moving towards the observer. That is, the observed frequency is increased whenever the source is moving toward the observer.

When the source moves away from a stationary observer, as in the case for observer \(B\) in the figure, the observer measures a wavelength \(\lambda ''\) that is greater than \(\lambda \) and hears a decreased frequency:
\[f'' = \left( {\frac{v}{{v + {v_s}}}} \right)f,\] where the source moving away from the observer.

Finally, we find the following general relationship for the observed frequency: \[f' = \left( {\frac{{v + {v_o}}}{{v - {v_s}}}} \right)f.\] In this expression, the signs for the values substituted for \({{v_o}}\) and \({{v_s}}\) depend on the direction of the velocity. A positive value is used for motion of the observer or the source toward the other, and a negative sign for motion of one away from the other.

The Doppler effect finds applications in a variety of fields. Following are a few applications of it.

1) The handheld radar gun used by traffic police to check for speeding vehicles relies on the Doppler effect. The officer aims his radar gun at an approaching vehicle. The gun sends out a burst of radio waves at a particular frequency. The radio waves strike the vehicle and bounce back toward the radar gun. The radar gun measures the frequency of the returning waves. Because the car is moving toward the gun, the frequency of the returning waves will be higher than the frequency of the waves initially transmitted by the gun. The faster the car's speed, the higher the frequency of the returning wave. By measuring the change in frequency of the rebounded wave, the speed of the vehicle can be measured.

2) Meteorologists use a similar principle to read weather events. In this case, the stationary transmitter is located in a weather station and the moving object being studied is a storm system.

3) Doppler echo-cardiogram: A traditional echo-cardiogram uses sound waves to produce images of the heart. The image produced by an echo-cardiogram shows the edges of heart structures, but it cannot measure the speed of blood flowing through the heart. Doppler techniques must be incorporated to provide this additional information. In a Doppler echo-cardiogram, sound waves of a certain frequency are transmitted into the heart. The sound waves bounce off blood cells moving through the heart and blood vessels. The movement of these cells, either toward or away from the transmitted waves, results in a frequency shift that can be measured. This helps cardiologists determine the speed and direction of blood flow in the heart.

4) Astronomers use Doppler effect to determine the movements of stars and planets which because of their far off distances from us and the consequent smallness of the parallactic angles are very difficult to measure. Any star or planet receding away from earth shows a decrease in frequency or increase in wavelength often called as red shift. The star or planet which is moving closer to earth shows increase in frequency or decrease in wavelength known as blue shift.

1. Doleron, . Doppler effect. Retrieved May 25, 2016, from https://commons.wikimedia.org/wiki/File:Doppler_Effect.gif