Dots and Boxes

We are holding an artificial intelligence contest in which participants need to develop a bot to play this game.

For more information, visit Brilliant Game Frame 1.0 - Dots and Boxes.

Dots and boxes is a classic, 2-player combinatorial strategy game. Then game starts with an empty $m \times n$ grid. During the game play, the players take turns to fill in lines joining two adjacent side either vertically or horizontally one at a time.

There are number of online apps available which provide online game stimulation like this and this.

The game starts with a grid containing $m \times n$ dots or $\left( m-1 \right) \left( n-1 \right)$ boxes. Players take turns while playing the game.

During each turn, a player draws a line joining two adjacent dots. The line must either be horizontal or vertical. If a player draws a line which completes a square, then the player earns points. If a square is completed by any player, then one more move needs to be completed by the same player. The goal of each player is to complete as many boxes as possible and earn maximum amount of points. This continues until no more moves can be made.

sample grid

The picture depicts a sample grid.

There is no standard game notation and thus the most convenient notation is used. In this wiki, we are going to use a modified version of chessboard notation to represent the lines.

sample notation

To identify each box, the following syntax is used - <name of the column><name of the row>. For example E1, A2, etc.

However, lines are more useful to be represented and identified using notation rather than boxes. Hence, to deal with this, every box notation is followed by a direction: T for top, B for bottom, R for right and L for left.

Hence every line can be written as <name of the column><name of the row><direction>. Examples: A1R, B7B, etc.

Warning: The above notation doesn't uniquely identify each line. Certain lines are shared by two boxes and as a result, certain lines can be represented by two different notations. For example, A2R and B2L represent the same line.

While programmatically representing the grid, we also need to store who wins each box. Here is a simple implementation you might consider using.

Example 1

Let's play a sample game on a $2 \times 2$ grid containing $3 \times 3$ dots.

-------

3x3 grid gameplay

All the moves described below are depicted in the image.

1) The game starts by player 1 playing first. Move: A2T

2) Player 2 plays next. Move: B1B

... (some trivial moves are ommited)

7) Player 1 plays next. Move: A1T. As a result, he opens up an opportunity for player 2 to complete a box.

8) Player 2 plays next. Move: A2R. Player 2 takes advantage of the opportunity and completes the A2 square. He earns one point. As a rule, after completing the square, player 2 needs to take another move. Move: B1T. As a result, he opens up lot of opportunities for player 1.

9) Player 1 plays next. Move: B2R. Player 1 completes the B2 square. As a rule, player 1 must take another move. Move: A1R. Player 1 got lucky and he completed another square B1. Again due to the rules, player 1 has to take another move. Move: A1L. This move is completes another square A1. Since no further moves can be made, game is complete. Points earned by player 1 in this game are 3.

Total score of player 1 is 3 while total score of player 2 is 1. Hence player 1 wins the game. $_\square$

Following the optimal strategy is a key to win any strategy game. Example 1 depicted the usage of a trivial strategy followed by player 1 in step 7 (where he sacrificed a box) to win the game. Some useful strategies employed are described below.

Minimax

---

The minimax algorithm is an algorithm which evaluates the value of a position in a combinatorial game by looking down the game tree based on the principle that the enemy aims to minimize the player's score while the player aims to maximize it. In theory, this algorithm should be able to play any game on $m \times n$ grid optimally. However, the algorithm is only implemented when the number of moves is less. This is because as the number of boxes on the grid increase, the total number of possibilities increase exponentially.

This algorithm is useful towards the end of the game.

Single double-box move

Another way of putting this is to say that if (and only if) $(m+1)(n+1)$ is odd, the first player wants to arrange things so that there is an even number of double-box moves in the game. For a chain of length 1 or 2, neither player need allow a double-box move to be made. However, in each chain of length 3 or more, either player may take all boxes but two, providing the opponent with a single double-box move. For a loop of four or more boxes, either player may take all but four boxes, providing the opponent with two double-box moves. Thus, in a well played game, the number of double-box moves is equal to the number of long chains, plus twice the number of loops, minus one because the player to move in the last long chain will take all of the boxes. So if $(m+1)(n+1)$ is odd, the first player wants an odd number of long chains in the game. Moreover, $(m+1)(n+1)$ is odd if and only if both m and n are even.

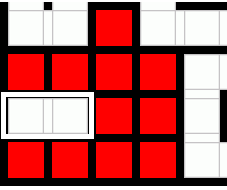
Providing the opponent with a single double box move only .. It is one of the best strategies , because if there are a long chains , if he gave you the small one , you can give him even a smaller size ( only double-box move permission)

Nimstring Analysis

---

This section is incomplete. Please help completing this section by editing the wiki.