Graphical Transformation of Trigonometric Functions

As we saw in sine and cosine graphs, the graphs of the basic sine and cosine functions are as follows:

Sine Function

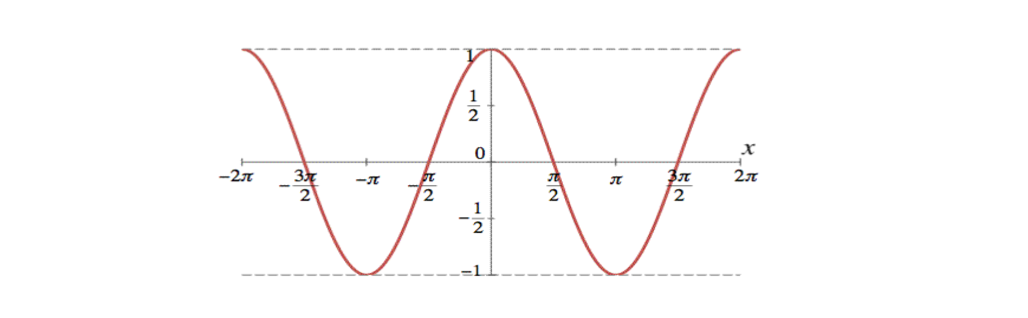Cosine Function

From these basic graphs, we can manipulate the functions to obtain new graphs by adding and multiplying by constants:

$$\begin{aligned} y &= a \sin (b x - c) + d\\ y &= a \cos (b x - c) + d. \end{aligned}$$

Let's consider how each of these constants changes the graph:

• $a:$ It stretches the graph vertically. This constant changes the amplitude of the graph, or half the distance from the top of the curve to the bottom of the curve. If $a$ is negative, then in addition to changing the amplitude, the graph will also be flipped horizontally.

• $b:$ It contracts or stretches the graph horizontally. Because the constant $b$ lies within the trigonometric function, this modifies the input (i.e. the $x$ values) and changes the period of the graph. If the graph is contracted, then the period becomes smaller; if the graph is stretched, then the period becomes larger. For example, the function $y = \cos(5x)$ contracts the graph horizontally by a factor of $5$, so the new period is $\frac{2\pi}{5}$.

• $c:$ It translates the graph horizontally. If $c$ is positive, then the graph is translated to the right; if $c$ is negative, then the graph is translated to the left. Note that this constant does not change the period or amplitude of the graph.

• $d:$ It translates the graph vertically. This constant is outside of the trigonometric function, so will change the values of the output $y$ by vertically shifting the graph. If $d$ is positive, then the graph will be shifted up; if $d$ is negative, then the graph will be shifted down. Note that this constant does not change the period or amplitude of the graph.

To gain some intuition about the period and horizontal shift, consider the value of $(bx -c)$ which is 0 and the value of $(bx - c)$ which is $2\pi$. This occurs for $x = \frac{c}{b}$ and $x = \frac{c}{b} + \frac{2\pi}{b}$, which shows why the horizontal shift is $\frac{c}{b}$ and the period is $\frac{2\pi}{b}$. To summarize, the resulting graph has

$$\text{horizontal shift: } \frac{c}{b}, \qquad \text{period: } \frac{2\pi}{b}.$$

What are the amplitude, period, shift, horizontal shift, and vertical shift of the function

$$y = -5 \cos \left( 4x - \frac{\pi}{3} \right) + 8.$$

---

Writing this in the form $y = a \cos (b x - c) + d$, we see that $a= -5, b=4, c=8, d = \frac{\pi}{3}$. The amplitude of the function is the absolute value of $a$, or 5. The period of the graph is $\frac{2\pi}{4} = \frac{\pi}{2}$. The horizontal shift of the graph is $c=\frac{\pi}{3},$ so the graph is translated to the right by $\frac{\pi}{3}$. Finally, the vertical shift of the graph is $d=8$, so the graph is shifted up by $8$. $_\square$

Find an equation for the following graph:

---

First, observe that the maximum value attained by the graph is $y=5$ and the minimum value attained by the graph is $y=-1$. This implies the amplitude of the graph is $\frac{5-(-1)}{2} = 3$, which implies the constant multiplying the trigonometric function is $3$. If we consider the sine function, then the vertical shift of the graph is the maximum value minus the amplitude, or $5 - 3 = 2.$ The period of the graph is $6\pi - (-2\pi) = 8\pi$.

One possible equation of the graph is then

$$3\sin \left(\frac{x}{4}-\pi \right)\ +2.\ _\square$$