Hyperbolic Trigonometric Functions
The hyperbolic trigonometric functions extend the notion of the parametric equations for a unit circle \((x = \cos t\) and \(y = \sin t)\) to the parametric equations for a hyperbola, which yield the following two fundamental hyperbolic equations:
\[x = \cosh a = \dfrac{e^a + e^{-a}}{2},\quad y = \sinh a = \dfrac{e^a - e^{-a}}{2}.\]
A very important fact is that the hyperbolic trigonometric functions take area as their argument (called "the hyperbolic angle," but this is just a name and has nothing to do with angles), as depicted below.

Hyperbolic functions show up in many real-life situations. For example, they are related to the curve one traces out when chasing an object that is moving linearly. They also define the shape of a chain being held by its endpoints and are used to design arches that will provide stability to structures. This shape, defined as the graph of the function \(y=\lambda \cosh \frac{x}{\lambda}\), is also referred to as a catenary.

 The St. Louis Gateway Arch—the shape of an upside-down hyperbolic cosine
The St. Louis Gateway Arch—the shape of an upside-down hyperbolic cosine
Hyperbolas, which are closely related to the hyperbolic functions, also define the shape of the path a spaceship takes when it uses the "gravitational slingshot" effect to alter its course via a planet's gravitational pull propelling it away from that planet at high velocity.
 The spaceship traces out a hyperbola as it uses the "slingshot" effect.
The spaceship traces out a hyperbola as it uses the "slingshot" effect.
Contents
Derivation of the Exponential Forms
One of the key characteristics that motivates the hyperbolic trigonometric functions is the striking similarity to trigonometric functions, which can be seen from Euler's formula:
\[\begin{align} e^{\pm i\theta} &= \cos\theta \pm i\sin\theta\\\\ \cos\theta &= \frac{e^{i\theta}+e^{-i\theta}}{2},\quad \sin\theta = \frac{e^{i\theta}-e^{-i\theta}}{2i}. \end{align}\]
In direct relation to these are the hyperbolic sine and cosine functions:
\[\cosh a = \frac{e^{a}+e^{-a}}{2},\quad \sinh a = \frac{e^{a}-e^{-a}}{2}.\]
These equations have their imaginary parts "ripped away." The proof of this is as follows:

Integrate \(\sqrt{x^{2}-1}\) from \(1\) to \(b\) to get the red area \((b\) is the distance from \(A\) to \(E):\)
\[\text{red area}=\displaystyle\int_1^b \sqrt{x^{2}-1} \, \mathrm dx =\dfrac{b\sqrt{b^{2}-1}-\ln \left(b+\sqrt{b^{2}-1}\right)}{2}.\]
Then subtract the red area from the area of the right triangle \(AED\) \(\big(\)which is \(\frac{1}{2}b\sqrt{b^{2}-1}\big)\) to get the area \(K:\)
\[\begin{align} K&=\dfrac{b\sqrt{b^{2}-1}}{2}-\dfrac{b\sqrt{b^{2}-1}-\ln \left(b+\sqrt{b^{2}-1}\right)}{2}\\ &=\dfrac{\ln \left(b+\sqrt{b^{2}-1}\right)}{2}. \end{align}\]
Imagine the reflection of \(K\) below the \(x\)-axis. That is, just set \(K=\frac{a}{2}:\)
\[a=\ln \left(b+\sqrt{b^{2}-1}\right).\]
Now solve for the base \(b\) which is the exponential form of the hyperbolic cosine:
\[x=b=\cosh a=\dfrac{e^{a}+e^{-a}}{2}.\]
After that, you can get the hyperbolic sine from \(\cosh ^{2}a-\sinh ^{2}a=1,\) which is obvious from \(x^{2}-y^{2}=1:\)
\[\begin{align} \sinh a&=\sqrt{\cosh ^{2}a-1}\\\\ y&=\sinh a\\ &=\dfrac{e^{a}-e^{-a}}{2}. \ _\square \end{align}\]
An alternative proof involves homogenous linear ODEs.
Express \(e^a\) and \(e^{-a}\) as functions of \(\sinh a\) and \(\cosh a.\)
Adding the two equations for \(\sinh a\) and \(\cosh a\) above yields
\[\begin{align} \cosh a + \sinh a &= \frac{e^{a}+e^{-a}}{2} + \frac{e^{a}-e^{-a}}{2}\\\\ \cosh a + \sinh a &= e^{a}. \qquad (1) \end{align}\]
Subtracting the two equations for \(\sinh a\) and \(\cosh a\) above yields
\[\begin{align} \cosh a - \sinh a &= \frac{e^{a}+e^{-a}}{2} - \frac{e^{a}-e^{-a}}{2}\\\\ \cosh a - \sinh a &= e^{-a}. \qquad (2) \end{align}\]
Combining equations (1) and (2), we get
\[e^{\pm a} = \cosh a \pm \sinh a,\]
which is the equivalent of Euler's formula for hyperbolic functions. \( _\square\)
Billy Tangent naively thought that the hyperbolic cosine function and the standard cosine function were the same. To make sure, he tried one real value and, sure enough, he got the same result.
What value did he try?
If you think there are multiple values for which this would work, enter 99999 as your answer.
If you think there are no values for which this would work, enter 88888 as your answer.
List of the Hyperbolic Trigonometric Functions
There are six hyperbolic trigonometric functions:
- \(\sinh x = \dfrac{e^x - e^{-x}}{2} \)
- \(\cosh x =\dfrac{e^x + e^{-x}}{2}\)
- \(\tanh x = \dfrac{\sinh x}{\cosh x}\)
- \(\coth x =\dfrac{1}{\tanh x}\)
- \(\text{sech}\, x =\dfrac{1}{\cosh x}\)
- \(\text{csch}\, y =\dfrac{1}{\sinh x}\).
Their graphic representations are shown here:
 Graphs of the six trigonometric hyperbolic functions
Graphs of the six trigonometric hyperbolic functions
Relationship to the Equations for a Unit Circle
The parametric equations for a unit circle are given by
- \(x = \cos t\)
- \(y = \sin t\).
As \(t\) goes from \(0 \rightarrow 2\pi\), \(x\) and \(y\) trace out the unit circle:
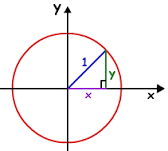
Similarly, the parametric equations for a unit hyperbola are given by
- \(x = \cosh a\)
- \(y = \sinh a\).
The blue line for positive \(x\) shows the line that this parametric set of equations traces out:

Show that hyperbolic cosine and hyperbolic sine functions form a set of parametric equations that translate into the equation for a hyperbola, \(x^2-y^2 = 1\).
Start with the hyperbolic functions:
\[x = \cosh a = \dfrac{e^a+e^{-a}}{2},\quad y = \sinh a = \dfrac{e^a-e^{-a}}{2}.\]
So,
\[x^2 = \dfrac{e^{2a}+2 + e^{-2a}}{4},\quad y^2 = \dfrac{e^{2a}-2 + e^{-2a}}{4},\]
which implies
\[\begin{align} x^2-y^2 &= \dfrac{e^{2a}+2 + e^{-2a}}{4} - \dfrac{e^{2a}-2 + e^{-2a}}{4} \\ &= \dfrac{2+2}{4}\\ &= 1.\ _\square \end{align}\]
Hyperbolic Trigonometric Identities
The hyperbolic sine and cosine are given by the following:
\[\cosh a = \frac{e^{a}+e^{-a}}{2},\quad \sinh a= \frac{e^{a}-e^{-a}}{2}.\]
The other hyperbolic trigonometric functions are defined in a similar way as the regular trigonometric functions:
\[\begin{align} \tanh a &= \frac{\sinh a}{\cosh a} = \frac{e^{a}-e^{-a}}{e^{a}+e^{-a}}\\\\ \coth a &= \frac{1}{\tanh a} = \frac{e^{a}+e^{-a}}{e^{a}-e^{-a}}\\\\ \text{sech } a &= \frac{1}{\cosh a}\\\\ \text{csch } a &= \frac{1}{\sinh a}. \end{align}\]
From these definitions, the following hyperbolic trigonometric identities can be derived which are strikingly similar to the standard trigonometric identites:
- \(\cosh x = \cosh (-x)\)
- \(\sinh x = - \sinh (-x)\)
- \(\tanh x = - \tanh (-x)\)
- \(\coth x = - \coth (-x)\)
- \(\text{sech} x = \text{sech} (-x)\)
\(\text{csch} x = - \text{csch} (-x)\)
\(\cosh^2 x - \sinh^2 x = 1 \)
- \(\tanh^2 x + \text{sech}^2 x = 1\)
- \(\coth^2 x - \text{csch}^2 x = 1\)
- \(\sinh (x + y) = \sinh x \cosh y + \cosh x \sinh y\)
- \(\sinh (x - y) = \sinh x \cosh y - \cosh x \sinh y\)
- \(\cosh (x + y) = \cosh x \cosh y + \sinh x \sinh y\)
- \(\cosh (x - y) = \cosh x \cosh y - \sinh x \sinh y\)
- \(\sinh^{2} x = \dfrac{-1 + \cosh (2x)}{2}\)
- \(\sinh (2x) = 2 \sinh x \cosh x\)
- \(\cosh^{2} x = \dfrac{1 + \cosh (2x)}{2}\)
- \(\cosh (2x) = \cosh^2 x + \sinh^2 x\).
Show that \(\cosh (2x) = \cosh^2 x + \sinh^2 x.\)
Start with the definitions of the hyperbolic sine and cosine functions:
\[\cosh x = \dfrac{e^{x}+e^{-x}}{2},\quad \sinh x = \dfrac{e^{x}-e^{-x}}{2}.\]
Therefore,
\[\begin{align} \cosh^2 x + \sinh^2 x &= \dfrac{e^{2x}+2+e^{-2x}}{4} + \dfrac{e^{2x}-2+e^{-2x}}{4}\\\\ &= \dfrac{e^{2x}+e^{-2x}}{2}\\\\ &= \cosh (2x).\ _\square \end{align}\]
Charley Brians was playing around with the following 6 trigonometric functions:
- \(\sin\)
- \(\cos\)
- \(\tan\)
- \(\cot\)
- \(\sec\)
- \(\csc\).
He noticed that, for one of them, if he sets it equal to its hyperbolic counterpart—\(\sinh, \cosh, \tanh, \coth, \text{sech},\) or \(\text{csch},\) respectively—it intersects at exactly four points.
Assuming that we are only dealing with real numbers, which trig function did he pick?
Inspiration: Brian Charlesworth
Shape of a Suspension Bridge
It has often been pondered whether the shape of a suspension bridge cable is a catenary or a parabola.

Now, if you hold up a piece of string, or a chain supported at both ends, it forms a catenary \(\big(y =\lambda \cosh \frac{x}{\lambda}\big).\) So, one might conclude that a suspension bridge assumes this shape.
However, what differentiates the bridge cable from a chain is that the bridge cable is not only holding up its own weight but also that of the bridge itself. So, let's consider two examples:
- where the weight of the bridge is negligible compared to the cable;
- where the weight of the support cable is negligible compared to that of the bridge.
Find the shape of the cable of a suspension bridge (pictured above) assuming the weight of the bridge is negligible compared to the weight of the cables.
If this is the case, then the problem is similar to that of a dangling chain.
Let the function of its shape be \(y(x)\), and WLOG define the low point of the chain to be at the origin.
Define the following:
- \(\mu =\) weight per unit length of the cable
- \(T =\) tension in the cable.

Define the following for a given point P:
- F = force along the cable whose direction will represent the slope of the cable at point P
- T = horizontal component of the cable tension
- W = the weight of the cable.
Clearly, the slope at P will be given by \[\text{Slope}= \frac{W}{T} = \frac{dy}{dx} = y'.\] If you consider a tiny segment \(s,\) then \[y' = \frac{\mu s}{T}.\] Dividing this into many tiny segments, \[dy' = \frac{\mu}{T}ds.\] Using the Pythagorean theorem, \[\begin{align} dy' &= \frac{\mu}{T}\sqrt{(dx)^2 + (dy)^2} = \frac{\mu}{T}\sqrt{(dx)^2 + (y'dx)^2} = \frac{\mu}{T}\sqrt{1 + (y')^2}dx\\\\ \Rightarrow y'' &= \frac{\mu}{T}\sqrt{1 + y'^2}. \end{align}\] Now, solving gives \[\frac{d(y')}{\sqrt{1+(y')^2}} = \frac{\mu\, dx}{T}.\] Integrating both sides, we get \[\sinh^{-1}(y') = \frac{\mu x}{T}.\] \(\big(\)No constant of integration, since the lowest point of the cable is at the origin, so \(y'(0) =0.\big)\)
Therefore, \[y' = \sinh \left(\frac{\mu x}{T}\right)\implies y = \frac{T}{\mu} \cosh\left(\frac{\mu x}{T}\right) + C. \] Again, no constant of integration since \(y(0) = 0,\) which implies \[y = \frac{T}{\mu} \cosh\left(\frac{\mu x}{T}\right).\] This can be simplified by setting \(\lambda =\frac{T}{\mu}\): \[y=\lambda \cosh \frac{x}{\lambda}.\ _\square\]
By the way, if you ever assumed that the curve of a dangling chain is parabolic, you aren't alone, as it is often said that Galileo also assumed the shape to be parabolic. This is not surprising as this figure shows the comparison between the two curves:

Now consider the shape of the suspension cable assuming that the weight of the cable is negligible compared to the weight of the bridge. This is quite a bit easier to solve since the weight of the bridge is now uniform in the \(x\) direction, whereas above it varied with the slope of the chain.
Find the shape of the cable of a suspension bridge (pictured above), assuming the weight of the cable is negligible compared to the weight of the bridge.
Lets define the same variables as before:
- \(\mu =\) weight per unit length of the cable
- \(T =\) tension in the cable
- F = force along the cable whose direction will represent the slope of the cable at point P
- T = horizontal component of the cable tension
- W = the weight of the cable.
As in the example above,
\[\text{Slope} = \frac{W}{T} = y'.\]
But this time, the mass density doesn't vary with the slope, and we'll assume that the density of the bridge is constant for its entire span. So,
\[\begin{align} \frac{W}{T} &= \mu\, dx\\ y' &= \frac{\mu x}{T}\\ \Rightarrow y &= \frac{\mu}{2T}x^2 +C. \end{align} \]
Once again, if we assume the low point of the cable is at the origin, then
\[y = \frac{\mu}{2T}x^2.\]
And after setting \(\lambda =\frac{T}{\mu}\) according to the previous example, we have
\[y=\frac{x^2}{2\lambda}.\ _\square\]
So, in conclusion, we see that if the cable supports only its own weight, like a rope being held at two points, it forms the shape of a catenary. However, if it has negligible weight relative to the bridge it supports, it assumes the shape of a parabola.
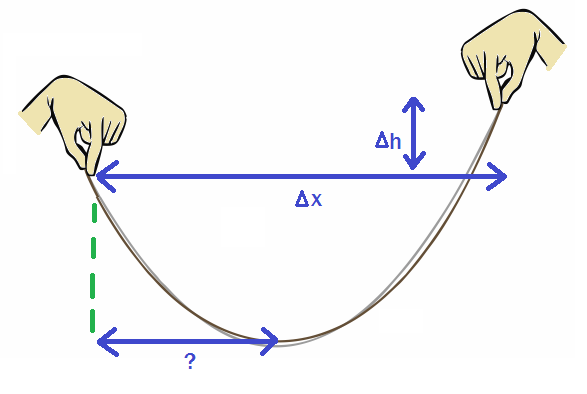
If you dangle a chain, as shown in the picture above, it forms a hyperbolic cosine function.
Assume the following values:
- \(\Delta h = 6\) inches
- \(\Delta x = 2\) feet.
What is the distance from the left (lower) side to the lowest point of the chain, in inches?
Give your answer to \(2\) decimal places.
If you think the answer can't be determined, please put 99999.
Image credit: https://methmath.wordpress.com