Integration
Integration is the process of evaluating integrals. It is one of the two central ideas of calculus and is the inverse of the other central idea of calculus, differentiation. Generally, we can speak of integration in two different contexts: the indefinite integral, which is the anti-derivative of a given function; and the definite integral, which we use to calculate the area under a curve.
Note that many integration problems will require the use of integration techniques.
Contents
Notations in Indefinite Integrals
Let \(f(x)\) and \(g(x)\) be functions related in such a way that
\[\int f(x)\ dx = g(x) + C.\]
- The integral sign \(\int\) denotes integration.
- \(f(x)\ dx\) is called the indefinite integral of \(f(x)\) with respect to \(x\).
- \(f(x)\) is called the integrand.
- The differential \(dx\) is part of the integrand; it identifies the variable used in integration.
- \(g(x) + C\) is called the general anti-derivative of \(f(x)\).
- \(C\) is called the constant of integration; it is an arbitrary constant.
- If \(C\) has a specific value from given conditions, \(g(x) + C\) is called a particular antiderivative.
Evaluating Indefinite Integrals
What is the anti-derivative of \(\left(x^2-1\right)^3?\)
Expanding the expression gives \(x^6 - 3x^4 + 3x^2 - 1 \). Applying the reverse power rule \(\int x^n \, dx = \frac1{n+1} x^{n+1} + C \) for \(n\ne-1,\) we have
\[\begin{align} \int \left(x^2-1\right)^3 \, dx &= \int \left(x^6 - 3x^4 + 3x^2 - 1\right) \, dx \\ \displaystyle &= \int x^6 \, dx - 3 \int x^4 \, dx + 3 \int x^2 \, dx - \int \, dx \\ \displaystyle &= \frac17 x^7 - \frac35x^5 + x^3 - x+ C, \end{align} \]
where \(C\) is the constant of integration. \((\)Note that \(\int \, dx = \int 1 \, dx = x + C.)\) \(_\square\)
What is the indefinite integral of \(e^{2x}?\)
Let \(y=e^{2x} \), then differentiating \(y\) with respect to \(x\) gives \(\frac{dy}{dx} = 2e^{2x} = 2y \), so \(dx = \frac{dy}{2y} \). Thus,
\[ \int e^{2x} \, dx = \int y \cdot \frac{dy}{2y} = \frac12 \int dy = \frac12 y + C = \frac12 e^{2x} + C,\]
where \(C\) is the constant of integration. \(_\square\)
What is the anti-derivative of \(x \ln x ?\)
Let \(x = e^y\), then \(y = \ln \, x\). Remember that
\[\frac{d \, (\ln \, x)}{dx} = \frac{1}{x}. \frac{d \, (\ln \, e^y)}{dx} = \frac{1}{e^y}.\]
Back to the function \(x \ln \, x \),
\[\frac{dy}{dx} = \frac{1}{e^y} \implies dy = \frac{dx}{e^y} \implies dx = e^y \, dy. \]
The integral now becomes
\[ \int e^y \, y \cdot e^y \, dy = \int y e^{2y} \, dy. \]
Integrating by parts, we let \(u = y \implies du = dy,\) and let \(dv = e^{2y} \, dy \implies v = \frac12 e^{2y}.\) Then
\[\begin{align} \int y e^{2y} \, dy &= \int u \, dv \\ \displaystyle &= uv - \int v \, du \\ \displaystyle &= \frac12 y e^{2y} - \frac12 \int e^{2y} \, dy \\ \displaystyle &= \frac12 y e^{2y} - \frac12 \cdot \frac12 e^{2y} + C \\ \displaystyle &= \frac12 x^2 \ln x - \frac14 x^2 + C, \end{align} \]
where \(C\) is the constant of integration. \(_\square\)
Definite Integrals
Evaluate \( \displaystyle \int_{\ln 2}^{\ln 5} e^{2x} \, dx. \)
From the previous example, we have \( \displaystyle\int e^{2x} \, dx = \frac12 e^{2x} + C .\)
Setting the upper and lower limits to be \(\ln 5 \) and \(\ln 2 \), respectively, the integral is evaluates to
\[ \left[ \frac12 e^{2x} \right]_{\ln 2}^{\ln 5} = \frac12 \cdot \left(5^2-2^2\right) = \frac{21}2 = 10.5. \ _\square \]
Evaluate the integral \(\displaystyle \int_{-1}^1 \left(x^2-1\right)^3 \, dx. \)
From the earlier example, the indefinite integral of \(\left(x^2-1\right)^3\) is given to be
\[ \frac17 x^7-\frac35x^5 + x^3 - x + C. \]
Applying the limits, we have
\[ \left [ \frac17 x^7\right]_{-1}^1 - \left[\frac35 x^5\right]_{-1}^1 + \left[x^3\right]_{-1}^1 - [x]_{-1}^1 =-\frac{32}{35}. \ _\square\]
Integration Techniques
Main Article: Integration by Parts and Integration with Partial Fractions
Find the anti-derivative of \(x \sin x\).
We should integrate by parts.
Using the LIATE (Logarithm, Inverse trigonometric, Algebraic, Trigonometric, Exponential) rules, we have \(u = x, dv = \sin x \, dx \implies du = dx, v = -\cos x.\) Hence,
\[ \begin{align} \int x \sin x \, dx & = \int u \, dv \\ &= uv - \int v du \\ &= -x \cos x + \int \cos x \, dx \\ &= -x \cos x + \sin x + C, \end{align} \]
where \(C\) is the constant of integration. \(_\square\)
Find the anti-derivative of \( \frac1{x(x+1)}. \)
By partial fraction decomposition, we have \( \frac1{x(x+1)} = \frac1x - \frac1{x+1} .\)
Recall that the anti-derivative of \( \frac1x \) is simply \( \ln|x| \), so the anti-derivative of the expression in question is
\[ \ln|x| - \ln|x+1| + C = \ln\left| \frac x{x+1} \right| + C,\]
where \(C\) is the constant of integration. \(_\square\)
Problem Solving - Basic
Verify by integration that the area of a circle with radius \(r\) is \( \pi r^2\).
By coordinate geometry, let the circle of radius \(r\) have its center at the origin, then the circle satisfies the equation \(x^2 + y^2 =r^2 \).
Rearranging gives \(y = \sqrt{r^2-x^2} \). We want to integrate from \(-r\) to \(r\) to get the area of the semicircle:
\[ \int_{-r}^r \sqrt{r^2-x^2} \, dx. \]
Let \(x = r \sin\theta\), then \(\frac{dx}{d\theta} = r\cos\theta.\) Here, \(\theta\) to ranges from \(-\frac{\pi}{2}\) to \(\frac{\pi}{2}.\) Then, the integral becomes
\[ \int_{-\frac\pi2}^{\frac\pi2} \sqrt{r^2-r^2\sin^2\theta} \cdot r\cos\theta \, dr = r^2 \int_{-\frac\pi2}^{\frac\pi2} \cos^2 \theta \,dr = r^2 \cdot \frac{\pi}{2}.\]
The integral of \(\cos^2\theta\) can be found via the half-angle substitution. Thus, the area of the circle is
\[2\cdot r^2 \cdot \frac{\pi}{2} = \pi r^2.\ _\square\]
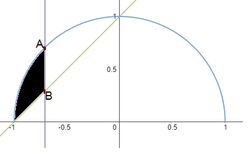 The figure at right shows a unit semicircle (in blue) and the graph of \(f(x)=x+1\) (in green).
The figure at right shows a unit semicircle (in blue) and the graph of \(f(x)=x+1\) (in green).
Let the purple line segment \(AB\) be the longest vertical line segment that joins the blue semicircle and green line in the domain \([-1,0].\)
If \(R\) is the area of the black shaded region, what is \(\left\lfloor 100R \right\rfloor ?\)
Problem Solving - Intermediate