Irregular Polygons
Polygons are two-dimensional geometric objects composed of points and straight lines connected together to close and form a single shape. Irregular polygons are polygons that have unequal angles and unequal sides, as opposed to regular polygons which are polygons that have equal sides and equal angles.
 Irregular Polygons
Irregular Polygons
As the concept of irregular polygons is extremely general, knowledge about this concept can be very valuable, both for problem solving and for simple problems in the real world. For example, this rug can be described as a single irregular polygon.
 An Irregular Polygon in the Wild
An Irregular Polygon in the Wild
Using the information in this wiki, the area of this rug could be easily calculated with a few measurements.
Contents
Simple and Self-intersecting Polygon
A simple polygon is a polygon in which no sides intersect each other.
Here are some examples of simple polygons:
Top to bottom, left to right: random polygon, kite, hexagon
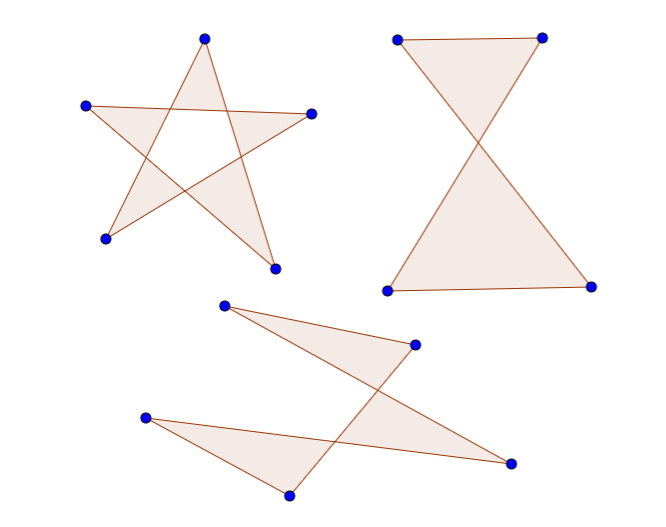
As opposed to a simple polygon, a self-intersecting polygon is a polygon that has at least one pair of sides crossing each other.
Here are some examples of self-intersecting polygons:
Convex and Concave Polygon
A convex polygon is a simple polygon that has all its interior angles less than \(180^\circ\)
As opposed to a convex polygon, a concave polygon is a simple polygon that has at least one interior angle greater than \(180^\circ\).
Classify these polygons as convex, concave, or neither.

We begin with polygon A. All of its angles are less than \(180^\circ\), so it is a convex polygon.
Polygon B has two sides which intersect, so it is a self-intersecting polygon, not a simple polygon. Therefore, it cannot be convex or concave, so it is neither.
Polygon C has one angle which is greater than \(180^\circ\), so it is concave.
Can a simple regular polygon be concave?
Which of these shapes can be a concave polygon?
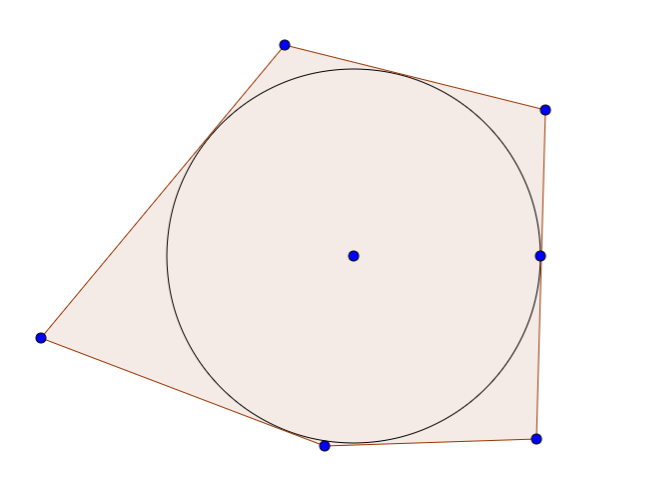
Cyclic and Tangential Polygon
A cyclic polygon is a polygon with vertices upon which a circle can be circumscribed. Every triangle is a cyclic polygon.

A tangential polygon is a simple polygon formed by the lines tangent to a circle. Similarly, every triangle is a tangential polygon.
Angle Sum Property
Main Article: General Polygons - Angles
For a simple \(n\)-gon, the sum of all interior angles is
\[S = (n-2)\times 180^\circ \quad \text{or} \quad S=(n-2)\times \pi \text{ rad}.\]
One of the proofs can be found in the Polygon Triangulation section.
Sameer has some geometry homework and is stuck with a question. The question says that the sum of the interior angles of a polygon doesn't exceed 2014 degrees.
What is the maximum possible number of sides of the polygon?
For any simple polygon, the sum of all exterior angles is \(360^\circ\). The proof of this is given below.
 A polygon has \( n \) sides. Two of its exterior angles are 72 degrees and 35 degrees, while the remaining exterior angles are each equal to 23 degrees.
A polygon has \( n \) sides. Two of its exterior angles are 72 degrees and 35 degrees, while the remaining exterior angles are each equal to 23 degrees.
Find the value of \( n \).
Perimeter of Irregular Polygon
Main Article: Perimeter
The perimeter of a two-dimensional figure is the length of the boundary of the figure. If the figure is a polygon, then the perimeter is the sum of all side lengths of the polygon.
What is the perimeter of a rectangle with width \(4\) and height \(7?\)
Since a rectangle has two sides with equal width and two sides with equal height, and the perimeter of a rectangle is the sum of its side lengths, the perimeter of the rectangle is
\[ 4 + 4 + 7 + 7 = 2(4) + 2(7) = 8 + 14 = 22 .\ _\square \]
 If the altitude and perimeter of the trapezium are \(3\) and \(A+B \sqrt{2}+C \sqrt{3},\) respectively, find \(A+B+C\).
If the altitude and perimeter of the trapezium are \(3\) and \(A+B \sqrt{2}+C \sqrt{3},\) respectively, find \(A+B+C\).
Area - Grid
A grid is useful to measure the area of an irregular polygon. The technique is to split the polygon into several basic shapes such as triangles and rectangles.

Above is a grid formed by \(1\times 1\) squares. What is the area of the polygon?

We split the polygon into several pieces. Independently computing the area of each piece, we have
\[\begin{aligned} A &= \frac{1}{2}\times 3\times 5 \\ &= 7\frac{1}{2} \\\\ B &= \frac{1}{2}\times 2\times 3 \\ &= 3 \\\\ C &= 3\times 3 \\ &= 9 \\\\ D &= 2\times 3 \\ &= 6. \end{aligned}\]
Finally, we add up all the small areas to get the overall area
\[A=7\frac{1}{2} +3+9+6=25\frac{1}{2}.\ _\square\]
Area - Pick's Theorem
Main article: Pick's Theorem
Pick's theorem provides a method to determine the area of any polygon whose vertices are points on a lattice.
Let \(P\) be a lattice polygon, and \(B(P)\) and \(I(P)\) be the number of points on the boundary and in the interior of the polygon, respectively. Then the area is
\[A= I(P) + \frac{1}{2} B(P) -1.\]
This is illustrated in the following example:
Consider a quadrilateral with verices \((1,1), (1,-1), (-1,-1), (-1,1).\) Find its area using Pick's theorem.
Let's calculate \(B(P)\) first.
On drawing the figure and counting the number of points on the boundary (with integer coordinates), we see that \(B(P)=8\).
Now, we see that the only interior point with integer coordinates is \((0,0)\). Hence \(I(P)=1\).
Therefore the area \((A)\) is given by
\[ A=(1) + \frac{1}{2} (8) - 1 = 4.\ _\square\]
Area - Coordinate Geometry
For an \(n\)-sided polygon, if we sort the points in a counterclockwise manner and let the coordinate of point \(i\) be \((x_i,y_i)\) and the area of the polygon be \(A\), we have
\[A = \frac{1}{2} \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \vdots & \vdots & \vdots \\ x_n & y_n & 1 \end{vmatrix}.\]
In other words,
\[A = \frac{1}{2} \sum_{i=1}^n \big ( x_iy_{i+1} - x_{i+1}y \big ).\]
Note that this is a generalization of the shoelace formula.
What is the area of the polygon with vertices at points \((1,1),(2,3),(0,5),(-1,0),(0,-3)?\)
By the shoelace formula,
\[A = \frac{1}{2} \begin{vmatrix} 1 & 1 & 1 \\ 2 & 3 & 1 \\ 0 & 5 & 1 \\ -1 & 0 & 1 \\ 0 & -3 & 1 \end{vmatrix}.\ _\square\]
Centroid
Main Article: Centroid
A centroid is the center of mass of a two-dimensional object with evenly distributed mass. The centroid of a simple polygon defined by \(n\) vertices \((x_0,y_0),(x_1,y_1),\dots,(x_n,y_n)\) is the point \((C_x,C_y)\) where
\[\begin{aligned} C_x &= \frac{1}{6A} \sum_{i=0}^{n-1} (x_i+x_{i+1})(x_iy_{i+1}-x_{i+1}y_i) \\ C_y &= \frac{1}{6A} \sum_{i=0}^{n-1} (y_i+y_{i+1})(x_iy_{i+1}-x_{i+1}y_i). \end{aligned}\]
Note that because the polygon has \(n\) vertices, \(x_0 = x_n\) and \(y_0=y_n\).
Polygon Triangulation
Main Article: Polygon Triangulation
Polygon triangulation is the process of decomposing a polygon into triangles. Every simple \(n\)-gon can be decomposed to \(n-2\) triangles. It immediately follows that the sum of interior angles in an \(n\)-gon is \((n-2)\times 180^\circ\).
 If we want to exactly cover a regular octagon with triangles (of any kind), what is the least number of triangles that we must use?
If we want to exactly cover a regular octagon with triangles (of any kind), what is the least number of triangles that we must use?
Art Gallery Problem
Main article: Art Gallery Problem
The art gallery problem studies the minimum number of guards needed to guard every point in the museum, the layout of which can be seen as a polygon. It turns out that any museum (polygon) with \(n\) walls (sides) can be guarded by at most \(\big\lfloor \frac{n}{3} \big\rfloor\) guards.

\(\)
Details and Assumptions: A point \(P\) in the museum is visible to a guard if the line segment from the guard to \(P\) lies within the triangle (or along the boundary).
See Guarding a Museum for more details on guarding a museum.
Problem Solving
In this section we will go through some examples related to irregular polygons, followed by problems to try yourself.

The interior angles of a convex polygon are in arithmetic progression. The smallest angle is \(120^\circ\) and the common difference is \(5^\circ\).
Find the number of sides of the polygon.
A hexagon is inscribed in a circle of radius \(r\). Two of its sides have length 1, another two have length 2, and the last two have length 3. If \(r\) is a root of \(ax^{3}+bx^{2}+cx+d=0\), where \(|a|, |c|\) and \(|d|\) are prime numbers, then find the value of \(|a|+|b|+|c|+|d|\).
This is a problem found in most math books for IIT JEE.

The figure to the right shows an irregular hexagon with six circles of radius 1, where the hexagon's vertices are the circles' centers.
Find the sum of the areas of the black regions.