Prime Numbers
A prime number is a natural number greater than 1 that has no positive integer divisors other than 1 and itself. For example, 5 is a prime number because it has no positive divisors other than 1 and 5.
The first 49 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, and 227.
In contrast to prime numbers, a composite number is a positive integer greater than 1 that has more than two positive divisors. For example, 4 is a composite number because it has three positive divisors: 1, 2, and 4. All positive integers greater than 1 are either prime or composite. 1 is the only positive integer that is neither prime nor composite.
Prime numbers are critical for the study of number theory. Nearly all theorems in number theory involve prime numbers or can be traced back to prime numbers in some way. Prime numbers are also important for the study of cryptography. The RSA method of encryption relies upon the factorization of a number into primes. Finally, prime numbers have applications in essentially all areas of mathematics. Prime numbers act as "building blocks" of numbers, and as such, it is important to understand prime numbers to understand how numbers are related to each other.
Contents
The Fundamental Theorem of Arithmetic
Main Article: Fundamental Theorem of Arithmetic
See Also: Prime Factorization
The fundamental theorem of arithmetic separates positive integers into two classifications: prime or composite.
Fundamental Theorem of Arithmetic
Every integer greater than 1 is either prime (it has no divisors other than 1 and itself) or composite (it has more than two divisors). Furthermore, every integer greater than 1 has a unique prime factorization up to the order of the factors.
The prime factorization of a positive integer is that number expressed as a product of powers of prime numbers. Prime factorizations are often referred to as unique up to the order of the factors. This means that each positive integer has a prime factorization that no other positive integer has, and the order of factors in a prime factorization does not matter.
Give the prime factorization of 48.
48 is divisible by the prime numbers 2 and 3. The highest power of 2 that 48 is divisible by is \(16=2^4.\) The highest power of 3 that 48 is divisible by is \(3=3^1.\) Thus, the prime factorization of 48 is
\[48=2^4 \times 3^1.\]
The fundamental theorem of arithmetic guarantees that no other positive integer has this prime factorization. \(_\square\)
Prime factorization is the primary motivation for studying prime numbers. Many theorems, such as Euler's theorem, require the prime factorization of a number. Prime factorization can help with the computation of GCD and LCM. Prime factorization is also the basis for encryption algorithms such as RSA encryption. In order to develop a prime factorization, one must be able to efficiently and accurately identify prime numbers.
Identifying Prime Numbers
The simplest way to identify prime numbers is to use the process of elimination. List out numbers, eliminate the numbers that have a prime divisor that is not the number itself, and the remaining numbers will be prime. This process can be visualized with the sieve of Eratosthenes.
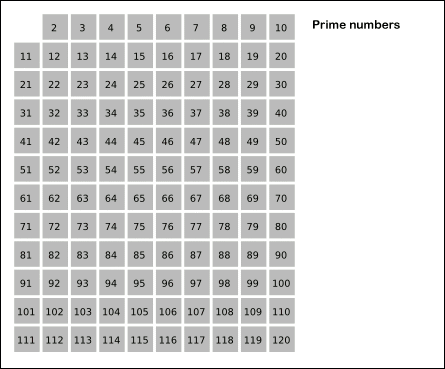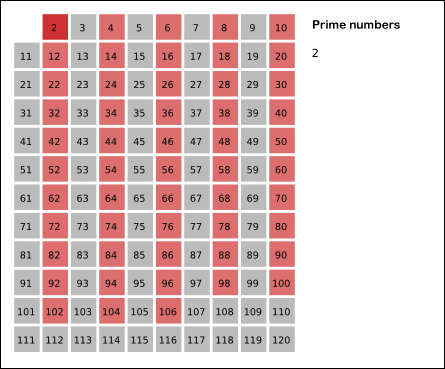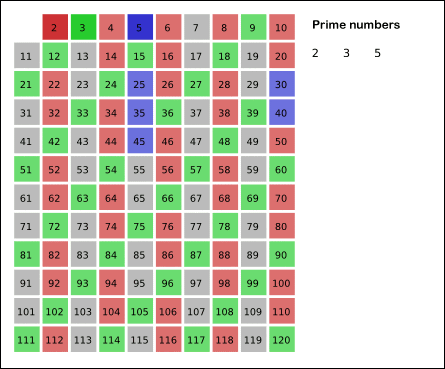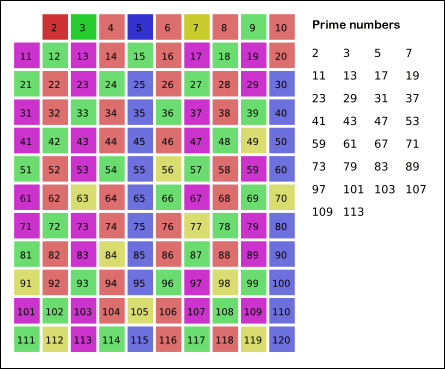 Sieve of Eratosthenes
Sieve of Eratosthenes
Another way to Identify prime numbers is as follows:
- First, choose a number, for example, 119.
- Now, note that prime numbers between 1 and 10 are 2, 3, 5, 7. (Why between 1 and 10? This question is answered in the theorem below.) Divide the chosen number 119 by each of these four numbers.
- If it's divisible by any of the four numbers, then it isn't a prime number; if it's not divisible by any of the four numbers, then it is prime.
- 119 is divisible by 7, so it is not a prime number.

Fortunately, one does not need to test the divisibility of each smaller prime to conclude that a number is prime. The number of primes to test in order to sufficiently prove primality is relatively small.
If \(n\) is a composite number, then it must be divisible by a prime \(p\) such that \(p \le \sqrt{n}.\)
Proof by Contradiction:
Suppose that \(n\) is a composite number, and it is only divisible by prime numbers that are greater than \(\sqrt{n}.\) Let two of its factors be \(q\) and \(r,\) with \(q,r > \sqrt{n}.\) Then \(n=kqr,\) where \(k\) is a positive integer. However, if \(q\) and \(r\) are both greater than \(\sqrt{n},\) then \(qr>n.\) This cannot be true, because \(n=kqr,\) and \(k\) is a positive integer. Thus, \(n\) must be divisible by a prime that is less than or equal to \(\sqrt{n}.\ _\square\)
One can apply divisibility rules to efficiently check some of the smaller prime numbers. Long division should be used to test larger prime numbers for divisibility. It is helpful to have a list of prime numbers handy in order to know which prime numbers should be tested.
Is 211 a prime number?
If 211 is a prime number, then it must not be divisible by a prime that is less than or equal to \(\sqrt{211}.\) \(\sqrt{211}\) is between 14 and 15, so the largest prime number that is less than \(\sqrt{211}\) is 13. It is therefore sufficient to test 2, 3, 5, 7, 11, and 13 for divisibility. 211 is not divisible by any of those numbers, so it must be prime. \(_\square\)
What is the sum of the two largest two-digit prime numbers?
If a two-digit number is composite, then it must be divisible by a prime number that is less than or equal to \(\sqrt{100}=10.\) Therefore, it is sufficient to test 2, 3, 5, and 7 for divisibility.
Counting backward,
- 99 is divisible by 3;
- 98 is divisible by 2;
- 97 is not divisible by 2, 3, 5, or 7, implying it is the largest two-digit prime number;
- 96 is divisible by 2;
- 95 is divisible by 5;
- 94 is divisible by 2;
- 93 is divisible by 3;
- 92 is divisible by 2;
- 91 is divisible by 7;
- 90 is divisible by 2;
- 89 is not divisible by 2, 3, 5, or 7, implying it is the second largest two-digit prime number.
The sum of the two largest two-digit prime numbers is \(97+89=186.\) \(_\square\)
What is the largest 3-digit prime number?
If a a three-digit number is composite, then it must be divisible by a prime number that is less than or equal to \(\sqrt{1000}.\) \(\sqrt{1000}\) is between 31 and 32, so it is sufficient to test all the prime numbers up to 31 for divisibility.
Counting backward, we have the following:
- 999 is the largest 3-digit number, but as it is divisible by \(3\), it is not prime.
- 998 is the second largest 3-digit number, but as it is divisible by \(2\), it is not prime.
- 997 is not divisible by any prime number up to \(31,\) so it must be prime. \(_\square\)
Which prime number follows 1997?
1998 is divisible by 2.
If 1999 is composite, then it must be divisible by a prime number that is less than or equal to \(\sqrt{1999}\). \(\sqrt{1999}\) is between 44 and 45, so the possible prime numbers to test are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, and 43. 1999 is not divisible by any of those numbers, so it is prime. \(_\square\)
Sometimes, testing a number for primality does not involve exhaustively searching for prime factors, but instead making some clever observation about the number that leads to a factorization. The next couple of examples demonstrate this.
In the following sequence, how many prime numbers are present?
\[121,12321,1234321,123454321,\ldots\]
We have
\[\begin{align} 121&= 11×11\\ 12321&= 111×111\\ 1234321&= 1111×1111\\ 123454321&= 11111×11111. \end{align}\]
So, no numbers in the given sequence are prime numbers. \(_\square\)
How many numbers in the following sequence are prime numbers?
\[101,10201,102030201,1020304030201, \ldots\]
We have the following factorization:
- \(101\) has no factors other than 1 and itself. So, it is a prime number.
- \(10201 = 101×101\).
- \(102030201 = 10101×10101\).
- \(1020304030201 = 1010101×1010101\).
So, there is only \(1\) prime number in the given sequence. \(_\square\)
Is 12345 a prime number?
We have \(\frac{12345}{5}=2469.\) So 12345 is divisible by 5 and therefore is not prime. \(_\square\)
Primality Tests
Main Article: Primality Testing
There are other methods that exist for testing the primality of a number without exhaustively testing prime divisors. These methods are called primality tests. One of these primality tests applies Wilson's theorem.
Wilson's Theorem
A positive integer \(p>1\) is prime if and only if
\[(p-1)! \equiv -1 \pmod{p}.\]
Show that 7 is prime using Wilson's theorem.
We have
\[\begin{align} 6!&=720\\ 720 &\equiv -1 \pmod{7}. \end{align}\]
Therefore, 7 must be prime. \(_\square\)
Testing primes with this theorem is very inefficient, perhaps even more so than testing prime divisors. However, this theorem does give insight that a number's primality is not linked purely to the divisors of that number. There are other "traces" in a number that can indicate whether the number is prime or not.
Most primality tests are probabilistic primality tests. These kinds of tests are designed to either confirm that the number is composite, or to use probability to designate a number as a probable prime. A probable prime is a number that has been tested sufficiently to give a very high probability that it is prime. An example of a probabilistic prime test is the Fermat primality test, which is based on Fermat's little theorem.
Fermat Primality Test
Given a positive integer \(n,\)
- Choose a positive integer \(a>1\) at random that is coprime to \(n\).
- Compute \(a^{n-1} \bmod {n}.\) If the result is not \(1,\) then \(n\) is composite. Otherwise, \(n\) may or may not be prime. If the result is \(1\) at this step, but \(n\) is composite, then \(n\) is pseudoprime to base \(a.\)
- Repeat these steps any number of times. Each repetition of these steps improves the probability that the number is prime. However, this process can never guarantee that a number is prime. A composite number that gets a result of \(1\) in the second step for all \(a\) less than \(n\) is called a Carmichael number.
Show that 91 is composite using the Fermat primality test with the base \(a=2\).
The goal is to compute \(2^{90}\bmod{91}.\)
Use the method of repeated squares. Compute 90 in binary:
\[90_{10}=1011010_{2}.\]
Compute the residues of the repeated squares of 2:
\[\begin{align} 2^{2^0} &\equiv 2 \pmod{91} \\ 2^{2^1} &\equiv 4 \pmod{91} \\ 2^{2^2} &\equiv 16 \pmod{91} \\ 2^{2^3} &\equiv 74 \pmod{91} \\ 2^{2^4} &\equiv 16 \pmod{91} \\ 2^{2^5} &\equiv 74 \pmod{91} \\ 2^{2^6} &\equiv 16 \pmod{91} \\ &\vdots\\ 2^{90} &= 2^{2^6} \times 2^{2^4} \times 2^{2^3} \times 2^{2^1} \\\\ 2^{90} &\equiv (16)(16)(74)(4) \pmod{91} \\ &\equiv 64 \pmod{91}. \end{align}\]
The result is not \(1.\) Therefore, \(91\) is not prime. \(_\square\)
This process might seem tedious to do by hand, but a computer could perform these calculations relatively efficiently. Thus, the Fermat primality test is a good method to screen a large list of numbers and eliminate numbers that are composite. Then, a more sophisticated algorithm can be used to screen the prime candidates further.
In general, identifying prime numbers is a very difficult problem. This, along with integer factorization, has no algorithm in polynomial time. In fact, it is so challenging that much of computer cryptography is built around the fact that there is no known computationally feasible way to find the factors of a large number.
Distribution of Primes
Main Article: Distribution of Primes
See Also: Infinitely Many Primes
It has been known for a long time that there are infinitely many primes. However, the question of how prime numbers are distributed across the integers is only partially understood. The prime number theorem gives an estimation of the number of primes up to a certain integer.
Prime Number Theorem
Let \(\pi(x)\) be the prime counting function. For any real number \(x,\) \(\pi(x)\) gives the number of prime numbers that are less than or equal to \(x.\) Then
\[\lim_{x \rightarrow \infty} \frac{\hspace{2mm} \pi(x)\hspace{2mm} }{\frac{x}{\ln{x}}}=1.\]
This implies that for sufficiently large \(x,\)
\[\pi(x) \sim \frac{x}{\ln{x}}.\]
There are many open questions about prime gaps. A prime gap is the difference between two consecutive primes. For example, the prime gap between 13 and 17 is 4. Bertrand's postulate gives a maximum prime gap for any given prime.
Bertrand's Postulate
For any integer \(n>3,\) there always exists at least one prime number \(p\) such that
\[n<p<2n-2.\]
This implies that for the \(k^\text{th}\) prime number, \(p_k,\) the next consecutive prime number is subject to
\[p_{k+1}<2p_k.\]
This is, unfortunately, a very weak bound for the maximal prime gap between primes. Prime gaps tend to be much smaller, proportional to the primes. For example, the first occurrence of a prime gap of at least 100 occurs after the prime 370261 (the next prime is 370373, a prime gap of 112).
The most famous problem regarding prime gaps is the twin prime conjecture. This conjecture states that there are infinitely many pairs of primes for which the prime gap is 2, but as of this writing, no proof has been discovered.
Another famous open problem related to the distribution of primes is the Goldbach conjecture. This conjecture states that every even integer greater than 2 can be expressed as the sum of two primes.
One of the most significant open problems related to the distribution of prime numbers is the Riemann hypothesis. Although the Riemann hypothesis has wide-reaching implications in number theory, Riemann's original motivation for formulating the conjecture was to better understand the distribution of prime numbers. The Riemann hypothesis relates the real parts of the zeros of the Riemann zeta function to the oscillations of the prime numbers about their "expected" positions given the estimation of the prime counting function above.
Mersenne Primes
Main Article: Mersenne Primes
A Mersenne prime is a prime that can be expressed as \(2^p-1,\) where \(p\) is a prime number.
The first five Mersenne primes are listed below:
\[\begin{array}{c|rr} p & 2^p-1= & M_p\\ \hline 2 & 2^2-1= & 3 \\ 3 & 2^3-1= & 7 \\ 5 & 2^5-1= & 31 \\ 7 & 2^7-1= & 127 \\ 13 & 2^{13}-1= & 8191 \end{array}\]
Note that having the form of \(2^p-1\) does not guarantee that the number is prime. \(2^{11}-1=2047\) is not a prime number; its prime factorization is \(23 \times 89.\)
From the list above, it might seem as though Mersenne primes are relatively easy to find by simply plugging in prime numbers into \(2^p-1\). However, Mersenne primes are exceedingly rare. As of January 2018, only 50 Mersenne primes are known, the largest of which is \(2^{77,232,917}-1\). This number is also the largest known prime number. In fact, many of the largest known prime numbers are Mersenne primes. This is due to the Lucas-Lehmer primality test, which is an efficient algorithm that is specific to testing primes of the form \(2^p-1\). Although Mersenne primes continue to be discovered, it is an open problem whether or not there are an infinite number of them.
Another notable property of Mersenne primes is that they are related to the set of perfect numbers. A perfect number is a positive integer that is equal to the sum of its proper positive divisors. Each Mersenne prime corresponds to an even perfect number:
Let \(M_p\) be a Mersenne prime. Then \(\frac{M_p\big(M_p+1\big)}{2}\) is an even perfect number. Furthermore, all even perfect numbers have this form.
Give the perfect number that corresponds to the Mersenne prime 31.
The perfect number is given by the formula above:
\[\frac{(31)(32)}{2}=496.\]
This number can be shown to be a perfect number by finding its prime factorization:
\[496=2^4\times 31.\]
Then listing out its proper divisors gives
\[\text{proper divisors of 496}=\{1,2,4,8,16,31,62,124,248\}.\]
Summing these divisors, we have
\[1+2+4+8+16+31+62+124+248=496.\ _\square\]
Number Theory Applications
One of the most fundamental theorems about prime numbers is Euclid's lemma.
Euclid's Lemma
Let \(p\) be prime. If \(p \mid ab\), then \(p \mid a\) or \(p \mid b\).
By Contradiction:
Suppose \(p\) does not divide \(a\). Since the only divisors of \(p\) are \(1\) and \(p,\) and \(p\) doesn't divide \(a,\) we must have \(\gcd (a, p) =1.\) By Bezout's identity, there exist some \(u\) and \(v\) such that \(ua+vp=1\). Multiplying both sides of this equation by \(b\) gives \(b=uab+vpb\). Now \(p\) divides \(uab\) \((\)since it is given that \(p \mid ab),\) and \(p\) also divides \(vpb\). Therefore, \(p\) divides their sum, which is \(b\). Without loss of generality, if \(p\) does not divide \(b,\) then it must divide \(a.\) \( _\square \)
Euclid's lemma can seem innocuous, but it is incredibly important for many proofs in number theory. For example, it is used in the proof that the square root of 2 is irrational.
Prime factorizations can be used to compute GCD and LCM.
GCD and LCM using Prime Factorizations
Given positive integers \(m\) and \(n,\) let their prime factorizations be given by
\[\begin{align} m&=p_1^{j_1} \times p_2^{j_2} \times p_3^{j_3} \times \cdots\\ n&=p_1^{k_1} \times p_2^{k_2} \times p_3^{k_3} \times \cdots, \end{align}\]
where \(p_1, p_2, p_3, \ldots\) are distinct primes and each \(j_i\) and \(k_i\) are integers.
Then the GCD of these integers is given by
\[\gcd(m,n)=p_1^{\min(j_1,k_1)} \times p_2^{\min(j_2,k_2)} \times p_3^{\min(j_3,k_3)} \times \cdots,\]
and the LCM of these integers is given by
\[\text{lcm}(m,n)=p_1^{\max(j_1,k_1)} \times p_2^{\max(j_2,k_2)} \times p_3^{\max(j_3,k_3)} \times \cdots.\]
Using prime factorizations, what are the GCD and LCM of 36 and 48?
The prime factorizations are
\[\begin{align} 36 &= 2^2 \times 3^2 \\ 48 &= 2^4 \times 3^1. \end{align}\]
Each number has the same primes, 2 and 3, in its prime factorization. The GCD is given by taking the minimum power for each prime number:
\[\begin{align} \gcd(36,48) &= 2^{\min(2,4)} \times 3^{\min(2,1)} \\ &= 2^2 \times 3^1 \\ &= 12. \end{align}\]
The LCM is given by taking the maximum power for each prime number:
\[\begin{align} \text{lcm}(36,48) &= 2^{\max(2,4)} \times 3^{\max(2,1)} \\ &= 2^4 \times 3^2 \\ &= 144.\ _\square \end{align}\]
Prime numbers are important for Euler's totient function.
Given a positive integer \(n\), Euler's totient function, denoted by \(\phi(n),\) gives the number of positive integers less than \(n\) that are co-prime to \(n.\)
What is \(\phi(10)?\)
Listing out the positive integers that are less than 10 gives
\[\{1,2,3,4,5,6,7,8,9\}.\]
Of those numbers, list the subset of numbers that are co-prime to 10:
\[\{1,3,7,9\}.\]
This set contains 4 elements. Therefore, \(\phi(10)=4.\ _\square\)
If \(n\) is a power of a prime, then Euler's totient function can be computed efficiently using the following theorem:
For any given prime \(p\) and positive integer \(n\),
\[\phi(p^n)=p^n-p^{n-1}.\]
Then, the value of the function for products of coprime integers can be computed with the following theorem:
Given co-prime positive integers \(m\) and \(n\),
\[\phi(mn)=\phi(m) \times \phi(n).\]
The consequence of these two theorems is that the value of Euler's totient function can be computed efficiently for any positive integer, given that integer's prime factorization.
What is \(\phi(48)?\)
The prime factorization of 48 is
\[48=2^4 \times 3^1.\]
Then,
\[\begin{align} \phi(2^4) &= 2^4-2^3=8 \\ \phi(3^1) &= 3^1-3^0=2 \\ &\vdots\\ \phi(48) &= 8 \times 2=16.\ _\square \end{align}\]
Euler's totient function is critical for Euler's theorem.
Euler's Theorem
Let \(a\) and \(n\) be coprime integers with \(n>0\). Then,
\[a^{\phi(n)} \equiv 1 \pmod{n}.\]
If \(n\) is a prime number, then this gives Fermat's little theorem.
Fermat's Little Theorem
Let \(p\) be a prime number and let \(a\) be an integer coprime to \(p.\) Then,
\[a^{p-1} \equiv 1 \pmod{p}.\]
The properties of prime numbers can show up in miscellaneous proofs in number theory.
Let \(p\) be a prime number greater than \(3\). Prove that \(p^2-1\) is always divisible by 6.
Any integer can be written in the form \(6k+n,\ n \in \{0,1,2,3,4,5\}\).
\(6k\) cannot be a prime.
\(6k+1\) may be a prime.
\(6k+2\) cannot be a prime.
\(6k+3\) cannot be a prime.
\(6k+4\) cannot be a prime.
\(6k+5\) may be a prime.
Thus, any prime \(p > 3\) can be represented in the form \(6k+5\) or \(6k+1\).
\(p^2-1\) can be factored to \((p+1)(p-1).\)
Case 1: \(p=6k+1\)
If this is the case, \(p^2-1=(6k+2)(6k),\) which implies \(6 \mid (p^2-1).\)Case 2: \(p=6k+5\)
If this is the case, \(p^2-1=(6k+6)(6k+4),\) which implies \(6 \mid (p^2-1).\)One of the factors, \(p-1\) or \(p+1\), will be divisible by \(6\). Thus, \(p^2-1\) is always divisible by \(6\). \(_\square\)
Additional Examples
\(n\) is the greatest prime number less than 50, and \(m\) is the least prime number greater than 50. What is the value of \(n+m?\)
Let's work backward for \(n\).
\(49\) is divisible by \(7\), and from the property of primes it is enough information to conclude that the number is not prime.
\(48\) is divisible by \(2,\) so cancel it.
When we look at \(47,\) it doesn't have any divisor other than one and itself. So it is indeed a prime: \(n=47.\)We use the same process in looking for \(m\).
\(51\) is divisible by \(3\).
\(52\) is divisible by \(2\).
\(53\) doesn't have any other divisor other than one and itself, so it is indeed a prime: \(m=53.\)Therefore, \[n+m=100.\ _\square\]
Consider the expression \(2^{n}-1,\) where \(n\) is an integer greater than \(1.\) What are the least two values of \(n\) for which the expression doesn't produce a prime number?
Let's check by plugging in numbers in increasing order.
- \(2^{2}-1=3\) is prime.
- \(2^{3}-1=7\) is prime.
- \(2^{4}-1=15\), which is divisible by 3, so it isn't prime.
- \(2^{5}-1=31\) is prime.
- \(2^{6}-1=63\), which is divisible by 7, so it isn't prime.
Therefore, the least two values of \(n\) are 4 and 6. \(_\square\)
Emirps
An emirp (prime spelled backwards) is a prime number that results in a different prime when its decimal digits are reversed. This definition excludes the related palindromic primes. The term reversible prime may be used to mean the same as emirp, but may also, ambiguously, include the palindromic primes.
The sequence of emirps begins 13, 17, 31, 37, 71, 73, 79, 97, 107, 113, 149, 157, 167, 179, 199, 311, 337, 347, 359, 389, 701, 709, 733, 739, 743, 751, 761, 769, 907, 937, 941, 953, 967, 971, 983, 991, ... (sequence A006567 in the OEIS).
All non-palindromic permutable primes are emirps.
As of November 2009, the largest known emirp is 1010006+941992101×104999+1, found by Jens Kruse Andersen in October 2007.
The term 'emirpimes' (singular) is used also in places to treat semiprimes in a similar way. That is, an emirpimes is a semiprime that is also a (distinct) semiprime upon reversing its digits.
