Johnson's Algorithm
Johnson's algorithm is a shortest path algorithm that deals with the all pairs shortest path problem. The all pairs shortest path problem takes in a graph with vertices and edges, and it outputs the shortest path between every pair of vertices in that graph. Johnson's algorithm is very similar to the Floyd-Warshall algorithm; however, Floyd-Warshall is most effective for dense graphs (many edges), while Johnson's algorithm is most effective for sparse graphs (few edges).
The reason that Johnson's algorithm is better for sparse graphs is that its time complexity depends on the number of edges in the graph, while Floyd-Warshall's does not. Johnson's algorithm runs in \(O\big(V^2 \cdot \log(V) + |V| \cdot |E|\big)\) time. So, if the number of edges is small (i.e. the graph is sparse), it will run faster than the \(O(V^3)\) runtime of Floyd-Warshall.
Johnson's algorithm is interesting because it uses two other shortest path algorithms as subroutines. It uses Bellman-Ford in order to reweight the input graph to eliminate negative edges and detect negative cycles. With this new, altered graph, it then uses Dijkstra's shortest path algorithm to calculate the shortest path between all pairs of vertices. The output of the algorithm is then the set of shortest paths in the original graph.
Contents
Overview
Johnson's algorithm works, as do many shortest path algorithms, on an input graph, \(G\). This graph has a set of vertices, \(V\), that map to a set of edges, \(E\). Each edge, \((u, v)\), has a weight function \(w = distance(u, v)\). Johnson's algorithm works on directed, weighted graphs. It does allow edges to have negative weights, but there can be no negative weight cycles (because then no shortest path would exist for vertices reachable by that cycle). It is interesting to note that Johnson's algorithm can support negative weight graphs because one of its subroutines, Dijkstra's algorithm, cannot.
Johnson's algorithm has three main steps.
- A new vertex is added to the graph, and it is connected by edges of zero weight to all other vertices in the graph.
- All edges go through a reweighting process that eliminates negative weight edges.
- The added vertex from step 1 is removed and Dijkstra's algorithm is run on every node in the graph.
These three steps can be seen in the graphic below. Figure (a) shows step 1. Figure (b) shows step 2. Figures (c)-(g) show step 3, Dijkstra's algorithm being run on each of the 5 vertices in the graph.
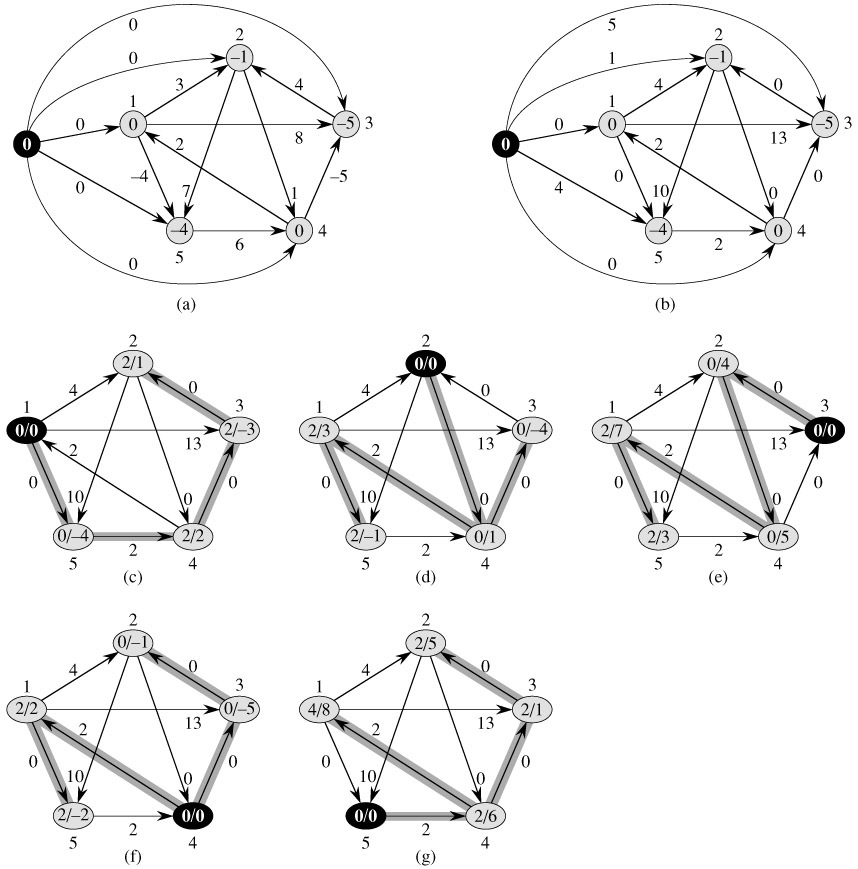 Johnson's Algorithm [1]
Johnson's Algorithm [1]
Algorithm Pseudocode
The following pseudo-code describes Johnson's algorithm at a high level. The subroutines are not explained because those algorithms already in the Bellman-Ford page and the Dijkstra page. To help you relate the pseudo-code back to the description of the algorithm, each of the three steps are labeled.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |
Algorithm Description
The three main parts of the algorithms are described below.
Step 1: adding a base vertex
The first part of the algorithm is fairly simple. Adding a new vertex, \(s\), to the graph and connecting it to all other vertices with a zero weight edge is easy given any graph representation method. A visual depiction of what happens is in the graphic below.
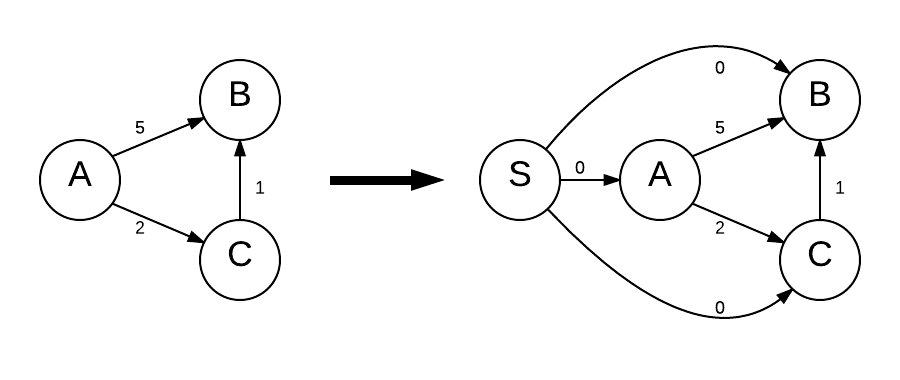 Step 1 of Johnson's algorithm
Step 1 of Johnson's algorithm
Step 2: Reweighting the edges
Reweighting is perhaps the most novel part of this algorithm. The basic concept is this: if all edges in a graph are non-negative, performing Dijkstra's algorithm on every vertex is the fastest way to solve the all-pairs shortest-path problem. If, however, some edges have negative weights, we can reweight them so that the following definition holds.
Reweighting is a process by which edge weight is changed to satisfy two properties.
- For all pairs of vertices u, v in the graph, if a certain path is the shortest path between those vertices before reweighting, it must also be the shortest path between those vertices after reweighting.
- For all edges, (u, v), in the graph, weight(u, v) must be non-negative.
This step uses Bellman-Ford to help reweight the edges. By using Bellman-Ford in this step, Johnson's algorithm is also able to detect negative weight cycles, a property of Bellman-Ford. The proof for reweighting can be found below.
Step 3: finding all pairs shortest path
Finally, Dijkstra's algorithm is run on all vertices to find the shortest path. This is possible because the weights have been transformed into non-negative weights. It is important, however, to transform these path weights back into the original path weights so that an accurate path weight is returned at the end of the algorithm. This is done at the end of the algorithm by simply reversing the reweighting process. Typically a data structure like a matrix is returned. At every cell \(i, j\) of this matrix is the shortest path from vertex \(i\) to vertex \(j\).
Reweighting Proof
To prove that the reweighting strategy is viable, both properties of reweighting must be proven to be true.
Property 1: preserving shortest paths
The first property states that a shortest path between any two vertices, \(u, v\) should remain the shortest path after reweighting. We will set out to prove the following equation preserves shortest paths. The function \(h(v)\) is a function that maps a vertex to number.
\[weight^{\prime}(u, v) = weight(u, v) + h(u) - h(v) .\]
Let \(p = {v_0, v_1, ..., v_k}\) be a path from \(v_0\) to \(v_k\). So, \(p\) is a shortest path with the original weight function if and only if it is a shortest path with the reweighted function. We have
\[weight^{\prime}(p) = weight(p) + h(v_0) - h(v_k) ,\] \[ = \sum_{i}^{k}weight^{\prime}(v_{i-1}, v_i) , \] \[ = \sum_{i}^{k}(weight(v_{i-1}, v_i) + h(v_{i-1}) - h(v_i)) ,\] due to telescoping sums, \[ = weight(p) + h(v_0) - h(v_k) .\]
So, any path from \(v_0\) to \(v_k\) that is a shortest path using the original weight function \(weight(p)\) is also a shortest path using the reweighting function \(weight^{\prime}(p)\). This is because \(h(v_0)\) and \(h(v_k)\) to not depend on the path.
Before we go on, it's important to also prove that any path \(p\) that has a negative weight cycle using the original weight function also has a negative weight cycle using the reweighted function (so we can detect negative weight cycles after the transformation).
Considering any cycle \(c\) and what we just proved in the step above, \[weight^{\prime}(c) = weight(c) + h(v_0) - h(v_k) ,\] \[ = weight(c) .\]
So, any cycle \(c\) that has a negative weight value before the transformation will also have one after reweighting.
Property 2: All reweighted edges must have a non-negative value
Remember how in step 1 of this algorithm, we constructed a new graph, \(G^{\prime}\) that had some important properties? It had an extra vertex, \(s\), that had edges going from it to all other vertices, and each of those edges had zero weight. An important consequence of this is that all shortest paths in this new graph will only contain \(s\) if \(s\) is the source (because there are no edges going into \(s\)).
Now, supposing \(G^{\prime}\) has no negative weight cycles (because we would know if it did), we can define \(h(v) = distance(s, v)\) for all \(v\) in \(G^{\prime}.V\). By the triangle inequality, we have
\[h(v) \leq h(u) + weight(u, v) ,\]
for all edges in \(G^{\prime}.E\). So, if we simply define our reweighting equation to be
\[weight^{\prime}(u, v) = weight(u, v) + h(u) - h(v) \geq 0 ,\]
then the second property is satisfied.
Complexity and Analysis
Johnson's algorithm runs in \(O(V^2log(V) + VE)\) time. This makes it asymptotically faster for sparse graphs than the Floyd-Warshall algorithm which runs in \(O(V^3)\) time.
See also: big O notation.
| Average | |
| Johnson's algorithm | \(O(V^2log(V) + VE)\) |
The analysis of Johnson's algorithm is straightforward if you understand the analyses of Bellman-Ford and Dijkstra's algorithm, so review those if you're a little rusty on them. It is important to note that in this analysis, the implementation of Dijkstra's algorithm will use a Fibonacci heap as its minimum priority queue, as it is the most efficient structure for the algorithm. Though, even using a simple minimum heap will yield a faster result than Floyd-Warshall.
The first step in the algorithm is simple and runs in \(O(V)\) time because it needs to make a new edge to all vertices in the graph. The second step of the algorithm, Bellman-Ford, runs in \(O(VE)\) time, as does Bellman-Ford. The process of reweighting the graph runs in the same time.
The final step of the algorithm is Dijkstra's algorithm run on all \(V\) vertices. Using a Fibonacci heap, each of these iterations takes \(O(V \log(V) + E)\) time to complete for a total complexity of \(O(V^2 \log(V) + VE)\). This is the dominating factor in the algorithm's complexity.
Note that if we were to use a minimum heap as the minimum priority queue in Dijkstra's algorithm, each iteration of Dijkstra would take \(O(E \log(V))\) time, for a total time complexity of \(O(VE \log(V))\).
References
- Leiserson, C. CLRS. Retrieved June 2, 2016, from http://citc.ui.ac.ir/zamani/clrs.pdf

