Lengths in Right Triangles
There are certain types of right triangles whose ratios of side lengths are useful to know. These are also found in specific values of trigonometric functions.
Isosceles Right Triangle
In an isosceles right triangle, the angles are \(45^\circ\), \(45^\circ\), and \(90^\circ\). For such a triangle, the two shorter sides of the triangle are equal in length and the hypotenuse is \(\sqrt{2}\) times the length of the shorter side:
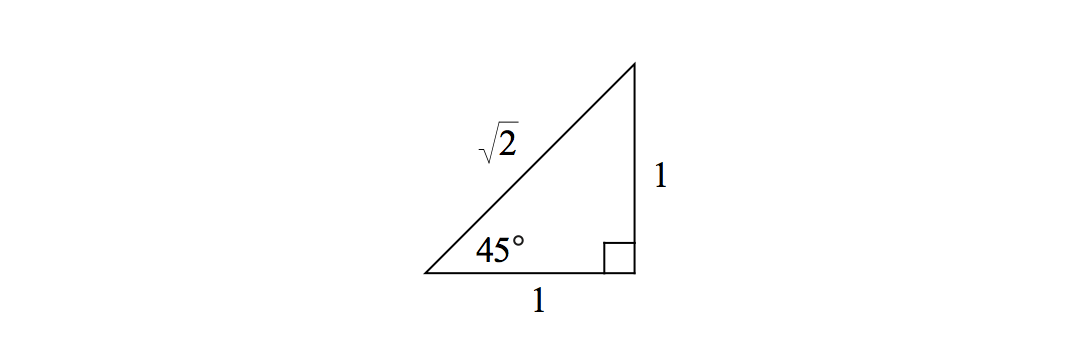
We can also see this relationship from the definition of \(\sin \theta\) and \(\cos \theta\) and using the specific value of \(\theta = 45^\circ\):
\[ \begin{align} \sin (45^\circ) &= \sin \left( \frac{\pi}{4} \right)= \frac{1}{\sqrt{2}} = \frac{\text{opposite}}{\text{hypotenuse}}\\\\ \cos (45^\circ) &= \cos \left( \frac{\pi}{4} \right)= \frac{1}{\sqrt{2}} = \frac{\text{adjacent}}{\text{hypotenuse}}. \end{align}\]
30-60-90 Right Triangle
In this right triangle, the angles are \(30^\circ, 60^\circ\), and \(90^\circ\).
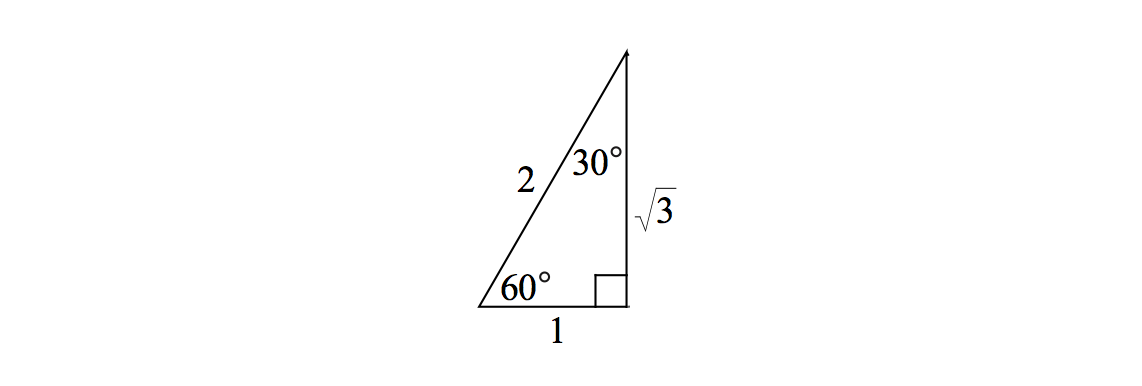
If the side opposite the \(30^\circ\) angle has length \(a\), then the side opposite the \(60^\circ\) angle has length \(a\sqrt{3}\) and the hypotenuse has length \(2a\). We can also see this from the definition of \(\sin \theta\) and \(\cos \theta\) and using the specific value of \(\theta = 60^\circ\):
\[ \begin{align} \sin (60^\circ) &= \sin \left( \frac{\pi}{3} \right)= \frac{\sqrt{3}}{2} = \frac{\text{opposite}}{\text{hypotenuse}}\\\\ \cos (60^\circ) &= \cos \left( \frac{\pi}{3} \right)= \frac{1}{2} = \frac{\text{adjacent}}{\text{hypotenuse}}. \end{align}\]
Right-angle Trigonometry
Consider the following right triangle:

Suppose we are given two side lengths of the triangle, for example, the hypotenuse \(c\) and the opposite side \(b\). Then we find the value of \(\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{b}{c}.\) From this, can we determine \(\cos(\theta)?\) Since the triangle is a right triangle, we can use the Pythagorean theorem to find the side length \(a,\) and from this we can find \(\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{a}{c}\). We illustrate this using an example.
Given the right triangle below

and two side lengths of the triangle \(a=3\) and \(b=4\), find \(\sin(\theta)\), \(\cos(\theta)\), and \(\tan(\theta)\).
Since \(\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{b}{a},\) we have \(\tan(\theta) = \frac{4}{3}.\) Also, the Pythagorean theorem implies that the hypotenuse \(c\) of the right triangle satisfies \(c^2 = a^2 + b^2 = 3^2 + 4^2 = 25 \), or \(c = 5\). Therefore,
\[\begin{align} \sin(\theta)&= \frac{b}{c} = \frac{4}{5}\\ \cos(\theta)&= \frac{a}{c} = \frac{3}{5}.\ _\square \end{align}\]
We will further investigate relationships between trigonometric functions on right triangles in the summary Pythagorean Identities.
Now, suppose we are given one of the acute angles in the right triangle and one of the sides of the triangle. Can we use the trigonometric functions to find the values of the other sides of the triangle?
Consider the following right triangle:

If the angle \(\theta \) equals \(\frac{\pi}{3}\) and side length \(a\) is \(5\), find the side length \(b\).
We have
\[\begin{align} \tan (\theta) = \tan \left( \frac{\pi}{3} \right) &= \frac{b}{a} \\ &= \frac{b}{5}\\ \sqrt{3} &= \frac{b}{5}\\ 5 \sqrt{3} &= b.\ _\square \end{align}\]