Basic Trigonometric Functions

Trigonometry comes from the two roots, trigonon (or “triangle”) and metria (or “measure”). The study of trigonometry is thus the study of measurements of triangles. What can we measure in a triangle? The first objects that come to mind may be the lengths of the sides, the angles of the triangle, or the area contained in the triangle. We first explore trigonometric functions that connect the measures of angles with the lengths of the sides.

The trigonometric functions relate the angles in a right triangle to the ratios of the sides. Given the following triangle:

$\hspace{4cm}$

the basic trigonometric functions are defined for $0 < \theta < \frac{\pi}{2}$ as

$$\begin{array}{c}&\sin \theta = \frac{b}{c}, &\cos \theta = \frac{a}{c}, &\tan \theta = \frac{b}{a}. \end{array}$$

If we consider the angle $\theta$ and label the sides with respect to $\theta$, then $a$ is the length of the "adjacent" side, $b$ is the length of the "opposite" side, and $c$ is the length of the hypotenuse. Then the basic trigonometric functions can be expressed as follows:

$$\begin{array}{c}&\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}, &\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}, &\tan \theta = \frac{\text{opposite}}{\text{adjacent}}. \end{array}$$

For a review of converting between degrees and radians, see Degrees and Radians. However, a more useful definition comes from the unit circle. If we consider a circle with a radius of 1 unit, centered at the origin, then the angle $\theta$ inside the circle describes a right triangle when we drop a perpendicular to the $x$-axis from the point of intersection with the circle.

Unit Circle

Notice that the right triangle so described has a hypotenuse equal to the radius of the circle, an adjacent side equal to the $x$-coordinate of the point $(x, y),$ and an opposite side equal to the $y$-coordinate. This gives rise naturally to the following refined definitions:

$$\begin{array}{c}&\sin \theta = \frac{y}{\text{radius}}, &\cos \theta = \frac{x}{\text{radius}}, &\tan \theta = \frac{y}{x}. \end{array}$$

As shown in the above diagram, since the radius is $1$ in the unit circle, this simplifies to $x= \cos \theta$ and $y= \sin \theta$.

These definitions have the advantage of being compatible with the triangle definition above, as well as allowing the evaluation of angles corresponding to any real number.

There are certain values of these functions which are useful to remember. They are:

$$\begin{array} {| c | c | c | c | c | c |} \hline \theta & 0^\circ & \frac{\pi}{6} = 30^\circ & \frac{\pi}{4} = 45^\circ & \frac{\pi}{3} = 60^\circ & \frac{\pi}{2} = 90^\circ\\ \hline \sin \theta & \frac {\sqrt{0}} {2} & \frac {\sqrt{1}} {2} & \frac {\sqrt{2}} {2} & \frac {\sqrt{3}} {2} & \frac {\sqrt{4}} {2} \\ \hline \cos \theta & \frac {\sqrt{4}} {2} & \frac {\sqrt{3}} {2} & \frac {\sqrt{2}} {2} & \frac {\sqrt{1}} {2} & \frac {\sqrt{0}} {2}\\ \hline \tan \theta & 0 & \frac { 1}{\sqrt{3} } & 1 & \sqrt{3} &\infty{} \\ \hline \end{array}$$

The reason for writing them in this way is to aid remembering these terms. For example, the numerator for $\sin \theta$ is simply the square root of $0, 1, 2, 3$ or $4.$ To visualize these values in the unit circle, see specific values of trigonometric functions.

What values of $\theta$ satisfy

$$\begin{array}{c}&0 \leq \theta < 2 \pi &\text{ and } &\cos \theta = 0? \end{array}$$

---

A good approach for a problem like this is to imagine the unit circle diagram shown above. In this unit circle diagram, $\cos\theta$ is the $x$-coordinate. Thus, the problem is asking for angle $\theta$ whose $x$-coordinate is equal to $0$, which occurs at the two points where the unit circle intersects the $y$-axis: $\theta = \frac{\pi}{2}$ and $\theta = \frac{3\pi}{2}$. Since these angles satisfy the given conditions, the two possible angles are $\theta = \frac{\pi}{2}$ and $\theta = \frac{3\pi}{2}$. $_\square$

If $\theta$ is an angle such that $\cos \theta = 0,$ what are the possible values of $\sin \theta$?

---

Solution 1:
As we saw above, $\cos\theta=0$ corresponds to points on the unit circle whose $x$-coordinate is $0$. Since these points occur at the points of intersection with the $y$-axis, the possible values of $\sin \theta$ are the possible $y$-coordinates, which are $1$ and $-1$. $_\square$

Solution 2:
From the first example, if $\cos \theta=0$ and $0 \leq \theta < 2 \pi$ , then $\theta=\frac{\pi}{2}$ or $\theta=\frac{3\pi}{2}$. Note that for all other values of $\theta$ outside of this range, we have $\sin \theta = \sin (\theta \pm 2\pi),$ so we can add or subtract multiples of $2\pi$ until $\theta$ lies in this range. For $\theta = \frac{\pi}{2}$, we have $\sin \theta = 1$ and for $\theta = \frac{3\pi}{2}$, we have $\sin \theta = -1$. Therefore, the possible values of $\sin \theta$ are $1$ and $-1$. $_\square$

If $\theta$ is an angle in a right triangle such that $\sin \theta = \frac{1}{2},$ what is the value of $\cos \theta$?

---

Since $\theta$ is an angle in a right triangle, it must be the case that $0 < \theta < \frac{\pi}{2}$.

From the table above, we see that the value $\theta$ such that $\sin (\theta)=\frac{1}{2}$ is $\theta =\frac{\pi}{6} = 30^{\circ}.$ Also, since the $y$-coordinate of the points on the unit circle are increasing as $\theta$ goes from $0$ to $\frac{\pi}{2}$, the value $\theta = \frac{\pi}{6}$ is the unique value such that $0 < \theta < \frac{\pi}{2}$ and $\sin \theta =\frac{1}{2}$. Then, we have $\cos \theta=\cos \frac{\pi}{2} =\frac{\sqrt{3}}{2}$. $_\square$

In the table of specific values for trigonometric functions above, why is there no value for $\tan \frac{\pi}{2}$? What happens to $\tan \theta$ as $\theta$ gets closer and closer to $\frac{\pi}{2}$?

---

From the above definition of $\tan\theta$, we have $\tan \theta=\frac{\sin \theta}{ \cos \theta} = \frac{y}{x}$, where $(x,y)$ are the $x$- and $y$-coordinates of the point of angle $\theta$ on the unit circle. As $\theta$ moves towards $\frac{\pi}{2}$, $\cos\theta$ (the $x$-coordinate) becomes smaller and smaller, whereas $\sin\theta$ (the $y$-coordinate) becomes closer and closer to $1$. Therefore, the numerator of $\tan \theta=\frac{y}{x}$ approaches $1$ and the denominator approaches $0$, implying $\tan \theta$ approaches infinity. $_\square$

To learn about the other trigonometric functions, read Reciprocal Trigonometric Functions and Inverse Trigonometric Functions.

There are certain values of the basic trigonometric functions which are useful to remember. They are:

$$\begin{array} {| c | c | c | c | c | c |} \hline \theta & 0^\circ & \frac{\pi}{6} = 30^\circ & \frac{\pi}{4} = 45^\circ & \frac{\pi}{3} = 60^\circ & \frac{\pi}{2} = 90^\circ\\ \hline \sin \theta & \frac {\sqrt{0}} {2} & \frac {\sqrt{1}} {2} & \frac {\sqrt{2}} {2} & \frac {\sqrt{3}} {2} & \frac {\sqrt{4}} {2} \\ \hline \cos \theta & \frac {\sqrt{4}} {2} & \frac {\sqrt{3}} {2} & \frac {\sqrt{2}} {2} & \frac {\sqrt{1}} {2} & \frac {\sqrt{0}} {2}\\ \hline \tan \theta & 0 & \frac { 1}{\sqrt{3} } & 1 & \sqrt{3} & \pm \infty \\ \hline \end{array}$$

The reason for writing them in this way is to aid remembering these terms. For example, the numerator for $\sin \theta$ is simply the square root of 0, 1, 2, 3, 4.

Visualization in Unit Circle

We can also visualize the cosine and sine values for these values in the unit circle:

Since the cosine function corresponds to $x$ values, the cosine function will be positive when $x$ values are positive and will be negative when $x$ values are negative. Similarly, since the sine function corresponds to $y$ values, the sine function will be positive when $y$ values are positive and will be negative when $y$ values are negative. This gives us the following behavior in the four quadrants of the plane:

Then by using the few specific values from the first quadrant, we can figure out the specific values of the cosine and sine functions in all quadrants. Here is the visualization for all quadrants:

Image courtesy commons.wikimedia.org

What are the values of $\theta$ in the range $0 \leq \theta < 2 \pi$ such that $\sin \theta = \cos \theta$?

---

From the unit circle visualization above, we see that $\theta = \frac{\pi}{4}$and $\theta = \frac{5\pi}{4}$ satisfy

$$\begin{aligned} \sin \left( \frac{\pi}{4} \right) &= \cos \left( \frac{\pi}{4} \right) = \frac{\sqrt{2}}{2}\\ \sin \left( \frac{5\pi}{4} \right) &= \cos \left( \frac{5\pi}{4} \right) = -\frac{\sqrt{2}}{2}. \end{aligned}$$

We also observe that the line $y=x$ intersects the unit circles for only these two values of $\theta$, so the values of $\theta$ satisfying the required conditions are $\theta = \frac{\pi}{4}$ and $\theta = \frac{5\pi}{4} .\ _\square$

What values of $\theta$ in the range $0 \leq \theta < 2 \pi$ satisfy $\sin \theta \geq \frac{\sqrt{2}}{2}$?

---

By drawing the line $y = \frac{\sqrt{2}}{2},$ we would like to find the values of $\theta$ such that the the $y$-value of the angle $\theta$ on the unit circle lies above this line (since $\sin \theta$ corresponds to the $y$-coordinate of the unit circle). This holds for $\theta\in \left[ \frac{\pi}{4}, \frac{3\pi}{4} \right]$, so these are the values of $\theta$ satisfying $\sin \theta \geq \frac{\sqrt{2}}{2}.\ _\square$

What are the values of $\theta$ in the range $0 \leq \theta < 2 \pi$ such that $\sin \theta = - \cos \theta$?

---

From the unit circle visualization above, we see that $\theta = \frac{3\pi}{4}$and $\theta = \frac{7\pi}{4}$ satisfy

$$\begin{aligned} \sin \left( \frac{3\pi}{4} \right) &= -\cos \left( \frac{3\pi}{4} \right) = \frac{\sqrt{2}}{2}\\ \sin \left( \frac{7\pi}{4} \right) &= - \cos \left( \frac{7\pi}{4} \right) = -\frac{\sqrt{2}}{2}. \end{aligned}$$

We also observe that the line $y=-x$ intersects the unit circle for only these two values of $\theta$, so the values of $\theta$ satisfying the required conditions are $\theta = \frac{3\pi}{4}$ and $\theta = \frac{7\pi}{4}.\ _\square$

In order to obtain further values, we will need to use some of the trigonometric formulas like sum and difference and product to sum. If you are unfamiliar with them, please skip this section for now and come back to it later.

Let us see an application of the sum and difference formulas.

Evaluate $\cos 15^ \circ$.

---

Using the difference formula for $\cos$, we have

$$\begin{aligned} \cos 15^\circ & = \cos (45 ^ \circ - 30 ^ \circ ) \\ & = \cos 45^\circ \cos 30 ^ \circ + \sin 45 ^ \circ \sin30 ^ \circ \\ & = \frac{ \sqrt{2} } { 2 } \times \frac{\sqrt{3}}{2} + \frac{ \sqrt{2} } { 2} \times \frac{1}{2} \\ & = \frac{ \sqrt{2} ( \sqrt{3} + 1 ) } { 4} \\ & = \frac{\sqrt{6} + \sqrt{2}} { 4}. \ _\square \end{aligned}$$

Let us see an application of the double angle formula.

Evaluate $\sin 15^\circ$.

---

We know that $\cos 30 ^ \circ = 1 - 2 \sin^2 15 ^ \circ$, so $\sin^2 15 ^ \circ = \frac{ 2- \sqrt{3} } { 4}$. Since $\sin 15^\circ$ is positive, we take the positive square root and get that

$$\sin 15^\circ = \frac { \sqrt{ 2 - \sqrt{3} } }{2}. \ _\square$$

How many integers $x$ are there such that $0 < x^\circ < 360$ and $2\sin^2 x^\circ < \sin x^\circ?$

---

We have $2\sin^2 x^\circ - \sin x^\circ = \sin x^\circ (2\sin x^\circ - 1) < 0$ or $0 < \sin x^\circ < \frac12$.

If we only consider the first quadrant, then $y = \sin x^\circ$ is an increasing function. So

$$0 = \sin 0^\circ < \sin 1^\circ < \sin 2^\circ < \cdots < \sin 29^\circ < \sin 30^\circ = \frac12,$$

which means there are 29 solutions.

Using the same argument, we have another 29 solutions in the second quadrant. This gives us a total of $29+29 =58$ solutions. $_\square$

If we know that $\tan 63^\circ < 2 < \tan 64^\circ$ and $\tan 84^\circ < 9 < \tan 85^\circ$, how many integers $x$ are there such that $0^\circ< x^\circ<90^\circ$ and $2 < \tan x^\circ < 9?$

---

Because $y = \tan x$ is an increasing function,

$$2 < \tan 64^\circ < \tan 65^\circ < \tan 66^\circ < \cdots < \tan 84^\circ < 9.$$

This gives us $84-64 + 1 = 21$ integer solutions of $x$. $_\square$

There are certain types of right triangles whose ratios of side lengths are useful to know. These are also found in specific values of trigonometric functions.

In an isosceles right triangle, the angles are $45^\circ$, $45^\circ$, and $90^\circ$. For such a triangle, the two shorter sides of the triangle are equal in length and the hypotenuse is $\sqrt{2}$ times the length of the shorter side:

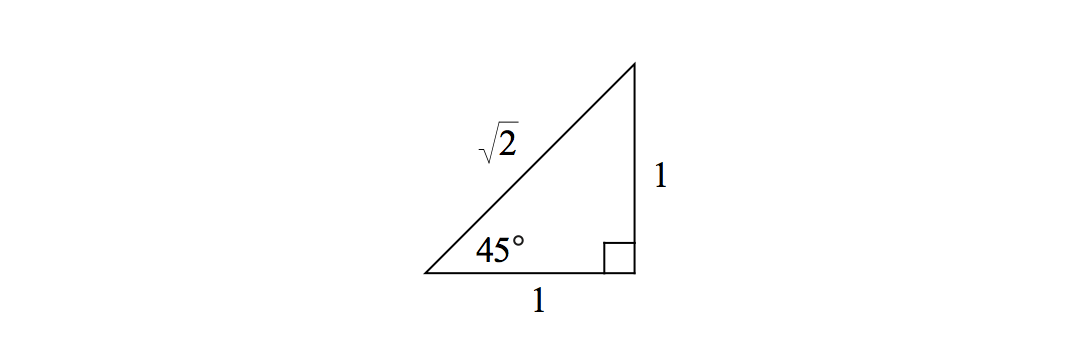
We can also see this relationship from the definition of $\sin \theta$ and $\cos \theta$ and using the specific value of $\theta = 45^\circ$:

$$\begin{aligned} \sin 45^\circ &= \sin \frac{\pi}{4}= \frac{1}{\sqrt{2}} = \frac{\text{opposite}}{\text{hypotenuse}}\\ \cos 45^\circ &= \cos \frac{\pi}{4}= \frac{1}{\sqrt{2}} = \frac{\text{adjacent}}{\text{hypotenuse}}. \end{aligned}$$

In this right triangle, the angles are $30^\circ, 60^\circ$, and $90^\circ$.

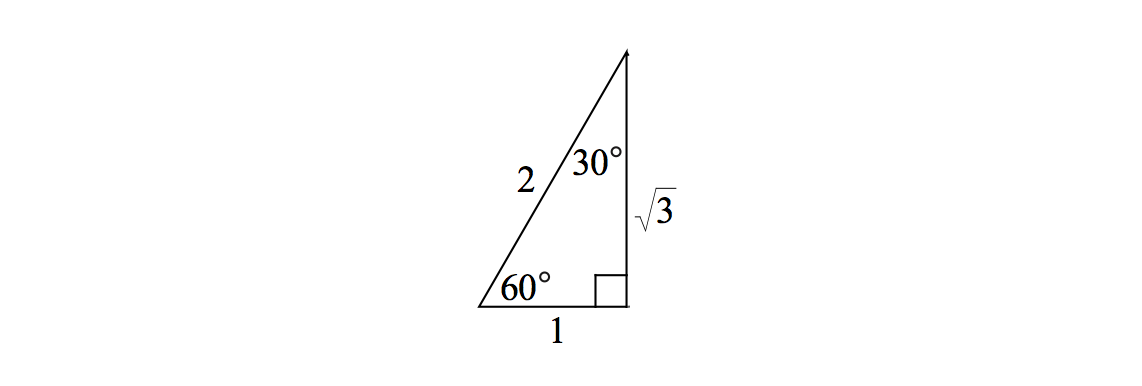
If the side opposite the $30^\circ$ angle has length $a$, then the the side opposite the $60^\circ$ angle has length $a\sqrt{3}$ and the hypotenuse has length $2a$. We can also see this from the definition of $\sin \theta$ and $\cos \theta$ and using the specific value of $\theta = 60^\circ$:

$$\begin{aligned} \sin 60^\circ &= \sin \left( \frac{\pi}{3} \right)= \frac{\sqrt{3}}{2} = \frac{\text{opposite}}{\text{hypotenuse}}\\ \cos 60^\circ &= \cos \left( \frac{\pi}{3} \right)= \frac{1}{2} = \frac{\text{adjacent}}{\text{hypotenuse}}. \end{aligned}$$

Consider the following right triangle:

Suppose we are given two side lengths of the triangle: for example, the hypotenuse $c$ and the opposite side $b$. Then we find

$$\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{b}{c}.$$

From this, can we determine $\cos \theta?$ Since the triangle is a right triangle, we can use the Pythagorean theorem to find the side length $a,$ and from this we can find

$$\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{a}{c}.$$

We illustrate this using an example:

In the right triangle below, two side lengths $a=3$ and $b=4$ are given. Find $\sin \theta$ and $\cos \theta.$

---

Since $\tan \theta = \frac{\text{opposite}}{\text{adjacent}} = \frac{b}{a},$ we have $\tan \theta = \frac{4}{3}.$ Also, the Pythagorean theorem implies that the hypotenuse $c$ of the right triangle satisfies $c^2 = a^2 + b^2 = 3^2 + 4^2 = 25$, or $c = 5$. Therefore,

$$\begin{aligned} \sin \theta&= \frac{b}{c} = \frac{4}{5}\\ \cos \theta&= \frac{a}{c} = \frac{3}{5}. \ _\square \end{aligned}$$

We will further investigate the relationships between trigonometric functions on right triangles in the wiki Pythagorean Identities.

Now, suppose we are given one of the acute angles in the right triangle and one of the sides of the triangle. Can we use the trigonometric functions to find the values of the other sides of the triangle?

Consider the following right triangle:

If angle $\theta$ equals $\frac{\pi}{3}$ and side length $a$ is $5$, find side length $b$.

---

We have

$$\begin{aligned} \tan \theta = \tan \left( \frac{\pi}{3} \right) = \frac{b}{a} &= \frac{b}{5}\\ \sqrt{3} &= \frac{b}{5}\\ b&=5 \sqrt{3}. \ _\square \end{aligned}$$