Limits of Functions
The limit of a function at a point \(a\) in its domain (if it exists) is the value that the function approaches as its argument approaches \(a.\) The concept of a limit is the fundamental concept of calculus and analysis. It is used to define the derivative and the definite integral, and it can also be used to analyze the local behavior of functions near points of interest.
Informally, a function is said to have a limit \( L \) at \( a \) if it is possible to make the function arbitrarily close to \( L \) by choosing values closer and closer to \( a \). Note that the actual value at \( a \) is irrelevant to the value of the limit.
The notation is as follows:
\[ \lim_{x \to a} f(x) = L, \]
which is read as "the limit of \(f(x) \) as \(x\) approaches \(a\) is \(L.\)"
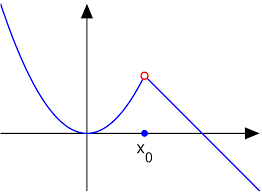 The limit of \( f(x) \) at \(x_0\) is the \(y\)-coordinate of the red point, not \(f(x_0).\) [1]
The limit of \( f(x) \) at \(x_0\) is the \(y\)-coordinate of the red point, not \(f(x_0).\) [1]
Contents
Formal Definition
Main Article: Epsilon-Delta Definition of a Limit
The precise definition of the limit is discussed in the wiki Epsilon-Delta Definition of a Limit.
Formal Definition of a Function Limit:
The limit of \(f(x)\) as \(x\) approaches \(x_0\) is \(L\), i.e.
\[\lim _{ x \to x_{0} }{f(x) } = L\]
if, for every \(\epsilon > 0 \), there exists \(\delta >0 \) such that, for all \(x\),
\[ 0 < \left| x - x_{0} \right |<\delta \textrm{ } \implies \textrm{ } \left |f(x) - L \right| < \epsilon. \]
In practice, this definition is only used in relatively unusual situations. For many applications, it is easier to use the definition to prove some basic properties of limits and to use those properties to answer straightforward questions involving limits.
Properties of Limits
The most important properties of limits are the algebraic properties, which say essentially that limits respect algebraic operations:
Suppose that \( \lim\limits_{x\to a} f(x) = M\) and \(\lim\limits_{x\to a} g(x) = N.\) Then
\[ \begin{align} \lim\limits_{x\to a} \big(f(x)+g(x)\big) &= M+N \\\\ \lim\limits_{x\to a} \big(f(x)-g(x)\big) &= M-N \\\\ \lim\limits_{x\to a} \big(f(x)g(x)\big) &= MN \\\\ \lim\limits_{x\to a} \left(\frac{f(x)}{g(x)}\right) &= \frac MN \ \ \text{ (if } N\ne 0) \\\\ \lim\limits_{x\to a} f(x)^k &= M^k \ \ \text{ (if } M,k > 0). \end{align} \]
These can all be proved via application of the epsilon-delta definition. Note that the results are only true if the limits of the individual functions exist: if \( \lim\limits_{x\to a} f(x) \) and \( \lim\limits_{x\to a} g(x)\) do not exist, the limit of their sum (or difference, product, or quotient) might nevertheless exist.
Coupled with the basic limits \( \lim_{x\to a} c = c,\) where \( c\) is a constant, and \( \lim_{x\to a} x = a,\) the properties can be used to deduce limits involving rational functions:
Let \( f(x) \) and \(g(x)\) be polynomials, and suppose \(g(a) \ne 0.\) Then
\[ \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{f(a)}{g(a)}. \]
This is an example of continuity, or what is sometimes called limits by substitution.
Note that \(g(a)=0\) is a more difficult case; see the Indeterminate Forms wiki for further discussion.
Let \(m\) and \(n\) be positive integers. Find
\[ \lim_{x\to 1} \frac{x^m-1}{x^n-1}. \]
Immediately substituting \(x=1\) does not work, since the denominator evaluates to \(0.\) First, divide top and bottom by \(x-1\) to get
\[\frac{x^{m-1}+x^{m-2}+\cdots+1}{x^{n-1}+x^{n-2}+\cdots+1}.\]
Plugging in \(x=1\) to the denominator does not give \(0,\) so the limit is this fraction evaluated at \(x=1,\) which is
\[\frac{1^{m-1}+1^{m-2}+\cdots+1}{1^{n-1}+1^{n-2}+\cdots+1} = \frac{m}{n}.\ _\square\]
It is important to notice that the manipulations in the above example are justified by the fact that \( \lim\limits_{x\to a} f(x)\) is independent of the value of \(f(x) \) at \(x=a,\) or whether that value exists. This justifies, for instance, dividing the top and bottom of the fraction \(\frac{x^m-1}{x^n-1}\) by \(x-1,\) since this is nonzero for \(x\ne 1.\)
One-sided Limits
A one-sided limit only considers values of a function that approaches a value from either above or below.
The right-side limit of a function \(f\) as it approaches \(a\) is the limit
\[\lim_{x \to a^+} f(x) = L. \]
The left-side limit of a function \(f\) is
\[\lim_{x \to a^-} f(x) = L. \]
The notation "\(x \to a^-\)" indicates that we only consider values of \(x\) that are less than \(a\) when evaluating the limit. Likewise, for "\(x \to a^+,\)" we consider only values greater than \(a\). One-sided limits are important when evaluating limits containing absolute values \(|x|\), sign \(\text{sgn}(x)\) , floor functions \(\lfloor x \rfloor\), and other piecewise functions.

The image above demonstrates both left- and right-sided limits on a continuous function \(f(x).\)
Find the left- and right-side limits of the signum function \(\text{sgn}(x)\) as \(x \to 0:\)
\[\text{sgn}(x)= \begin{cases} \frac{|x|}{x} && x\neq 0 \\ 0 && x = 0. \end{cases}\]
Consider the following graph:

From this we see \(\displaystyle \lim_{x \to 0^+} \text{sgn}(x) = 1 \) and \(\displaystyle \lim_{x \to 0^-}\text{sgn}(x) = -1.\ _\square \)
Determine the limit \( \lim\limits_{x \to 1^{-}} \frac{\sqrt{2x}(x-1)}{|x-1|}. \)
Note that, for \(x<1,\) \(\left | x-1\right |\) can be written as \(-(x-1)\). Hence, the limit is \(\lim\limits_{x \to 1^{-}} \frac{\sqrt{2x}(x-1)}{-(x-1)} = -\sqrt{2}.\ _\square\)
Two-sided Limits
By definition, a two-sided limit
\[\lim_{x \to a} f(x) = L\]
exists if the one-sided limits \(\displaystyle \lim_{x \to a^+} f(x)\) and \(\displaystyle \lim_{x \to a^-} f(x)\) are the same.
Compute the limit
\[ \lim_{x \to 1} \frac{|x - 1|}{x - 1} . \]
Since the absolute value function \(f(x) = |x| \) is defined in a piecewise manner, we have to consider two limits: \(\lim\limits_{x \to 1^+} \frac{|x - 1|}{x - 1} \) and \(\lim\limits_{x \to 1^-} \frac{|x - 1|}{x - 1}. \)
Start with the limit \(\lim\limits_{x \to 1^+} \frac{|x - 1|}{x - 1}.\) For \(x>1,\) \( |x - 1| = x -1. \) So
\[\lim_{x \to 1^+} \frac{|x - 1|}{x - 1} =\lim_{x \to 1^+} \frac{x - 1}{x - 1} =1.\]
Let us now consider the left-hand limit
\[\lim_{x \to 1^-} \frac{|x - 1|}{x - 1}. \]
For \(x<1,\) \(x - 1 = -|x-1|.\) So
\[\lim_{x \to 1^-} \frac{|x-1|}{-|x - 1|} = -1 . \]
So the two-sided limit \( \lim\limits_{x \to 1} \frac{|x - 1|}{x - 1}\) does not exist. \(_\square\)
The image below is a graph of a function \(f(x)\). As shown, it is continuous for all points except \(x = -1\) and \(x=2\) which are its asymptotes. Find all the integer points \(-4 <I < 4,\) where the two-sided limit \(\lim_{x \to I} f(x)\) exists.
image
Since the graph is continuous at all points except \(x=-1\) and \(x=2\), the two-sided limit exists at \(x=-3\), \(x=-2\), \(x=0\), \(x=1,\) and \(x=3\). At \(x=2,\) there is no finite value for either of the two-sided limits, since the function increases without bound as the \(x\)-coordinate approaches \(2\) (but see the next section for a further discussion). The situation is similar for \(x=-1.\) So the points \(x=-3\), \(x=-2\), \(x=0\), \(x=1,\) and \(x=3\) are all the integers on which two-sided limits are defined. \(_\square\)
Infinite Limits
As seen in the previous section, one way for a limit not to exist is for the one-sided limits to disagree. Another common way for a limit to not exist at a point \(a\) is for the function to "blow up" near \(a,\) i.e. the function increases without bound. This happens in the above example at \(x=2,\) where there is a vertical asymptote. This common situation gives rise to the following notation:
Given a function \(f(x)\) and a real number \(a,\) we say
\[\lim_{x\to a} f(x) = \infty.\]
If the function can be made arbitrarily large by moving \(x\) sufficiently close to \(a,\)
\[\text{for all } N>0, \text{ there exists } \delta>0 \text{ such that } 0<|x-a|<\delta \implies f(x)>N.\]
There are similar definitions for one-sided limits, as well as limits "approaching \(-\infty\)."
Warning: If \(\lim\limits_{x\to a} f(x) = \infty,\) it is tempting to say that the limit at \(a\) exists and equals \(\infty.\) This is incorrect. If \(\lim\limits_{x\to a} f(x) = \infty,\) the limit does not exist; the notation merely gives information about the way in which the limit fails to exist, i.e. the value of the function "approaches \(\infty\)" or increases without bound as \(x \rightarrow a\).
What can we say about \(\lim\limits_{x \to 0} \frac{1}{x}?\)
Separating the limit into \(\lim\limits_{x \to 0^+} \frac{1}{x}\) and \(\lim\limits_{x \to 0^-} \frac{1}{x}\), we obtain
\[ \lim_{x \to 0^+} \frac{1}{x} = \infty \]
and
\[ \lim_{x \to 0^-} \frac{1}{x} = -\infty. \]
To prove the first statement, for any \(N>0\) in the formal definition, we can take \(\delta = \frac1N,\) and the proof of the second statement is similar.
So the function increases without bound on the right side and decreases without bound on the left side. We cannot say anything else about the two-sided limit \(\lim\limits_{x\to a} \frac1{x} \ne \infty\) or \(-\infty.\) Contrast this with the next example. \(_\square\)
What can we say about \(\lim\limits_{x \to 0} \frac{1}{x^2}?\)
Separating the limit into \(\lim\limits_{x \to 0^+} \frac{1}{x^2}\) and \(\lim\limits_{x \to 0^-} \frac{1}{x^2}\), we obtain
\[ \lim_{x \to 0^+} \frac{1}{x^2} = \infty \]
and
\[ \lim_{x \to 0^-} \frac{1}{x^2} = \infty.\]
Since these limits are the same, we have \( \lim_{x \to 0} \frac{1}{x^2} = \infty .\) Again, this limit does not, strictly speaking, exist, but the statement is meaningful nevertheless, as it gives information about the behavior of the function \( \frac1{x^2}\) near \(0.\) \(_\square\)
Let
\[f(x)=\frac{a_0 x^{m}+a_1 x^{m+1}+\cdots +a_k x^{m+k}}{b_0 x^{n}+b_1 x^{n+1}+\cdots +b_ l x^{n+l}},\]
where \(a_0 \neq 0, b_0 \neq 0,\) and \(m,n \in \mathbb N.\)
Then given (A), (B), (C), or (D), \(\displaystyle\lim_{x\rightarrow 0}f(x)\) equals which of (1), (2), (3), and (4)?
Match the columns:
| Column-I | Column-II |
| (A) if \(m>n\) | (1) \(\infty\) |
| (B) if \(m=n\) | (2) \(-\infty\) |
| (C) if \(m<n,\) \(n-m\) is even, and \(\frac{a_0}{b_0}>0\) \(\hspace{10mm}\) | (3) \(\frac{a_0}{b_0}\) |
| (D) if \(m<n,\) \(n-m\) is even, and \(\frac{a_0}{b_0}<0\) \(\hspace{10mm}\) | (4) \(0\) |
Note: For example, if (A) correctly matches (1), (B) with (2), (C) with (3), and (D) with (4), then answer as 1234.
Limits at Infinity
Another extension of the limit concept comes from considering the function's behavior as \(x\) "approaches \(\infty\)," that is, as \(x\) increases without bound.
The equation \( \lim\limits_{x\to\infty} f(x) = L\) means that the values of \(f\) can be made arbitrarily close to \(L\) by taking \(x\) sufficiently large. That is,
\[\text{for all } \epsilon > 0, \text{ there is } N>0 \text{ such that } x>N \implies |f(x)-L|<\epsilon.\]
There are similar definitions for \(\lim\limits_{x\to -\infty} f(x) = L,\) as well as \(\lim\limits_{x\to\infty} f(x) = \infty,\) and so on.
Graphically, \(\lim\limits_{x\to a} f(x) = \infty\) corresponds to a vertical asymptote at \(a,\) while \( \lim\limits_{x\to\infty} f(x) = L \) corresponds to a horizontal asymptote at \(L.\)
Limits by Factoring
Main Article: Limits by Factoring
Limits by factoring refers to a technique for evaluating limits that requires finding and eliminating common factors.
Limits by Substitution
Main Article: Limits by Substitution
Evaluating limits by substitution refers to the idea that under certain circumstances (namely if the function we are examining is continuous), we can evaluate the limit by simply evaluating the function at the point we are interested in.
L'Hôpital's Rule
Main Article: L'Hôpital's Rule
L'Hôpital's rule is an approach to evaluating limits of certain quotients by means of derivatives. Specifically, under certain circumstances, it allows us to replace \( \lim \frac{f(x)}{g(x)} \) with \( \lim \frac{f'(x)}{g'(x)}, \) which is frequently easier to evaluate.
Limits of Functions - Problem Solving
Evaluate \( \lim\limits_{x\to\infty} \frac{x^2 + 2x +4}{3x^2+ 4x+125345} \).
We have
\[\begin{eqnarray} &&\displaystyle \lim_{x\to\infty} \frac{x^2 + 2x +4}{3x^2+ 4x+125345} &=& \displaystyle \lim_{x\to\infty} \frac{1 + \frac2x + \frac4{x^2}}{3+ \frac4x+ \frac{125345}{x^2}} &=& \displaystyle \frac{1+0+0}{3+0+0} = \frac13.\ _\square \end{eqnarray} \]
References
- Alexandrov, O. Discontinuity. Retrieved September 12, 2005, from https://commons.wikimedia.org/wiki/File:Discontinuity_removable.eps.png
