Linked List

Linked lists are linear data structures that hold data in individual objects called nodes. These nodes hold both the data and a reference to the next node in the list.

Linked lists are often used because of their efficient insertion and deletion. They can be used to implement stacks, queues, and other abstract data types.

You can visualize a linked list using the following image:

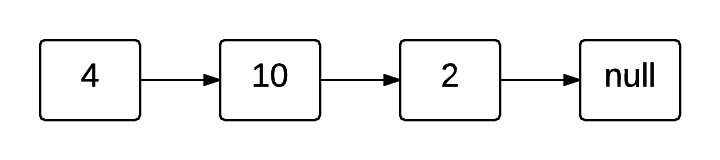Linked List

Each node contains a value--in this case, an integer--and a reference (also known as a pointer) to the next node. The last node, in this case 2, points to a null node. This means the list is at its end.

Linked lists offer some important advantages over other linear data structures. Unlike arrays, they are a dynamic data structure, resizable at run-time. Also, the insertion and deletion operations are efficient and easily implemented.

However, linked lists do have some drawbacks. Unlike arrays, linked lists aren't fast at finding the \(n^\text{th}\) item. To find a node at position \(n\), you have to start the search at the first node in the linked list, following the path of references \(n\) times. Also, because linked lists are inherently sequential in the forward direction, operations like backward traversal--visiting every node starting from the end and ending in the front--is especially cumbersome.

Additionally, linked lists use more storage than the array due to their property of referencing the next node in the linked list.

Finally, unlike an array whose values are all stored in contiguous memory, a linked list's nodes are at arbitrary, possibly far apart locations in memory. This means that the CPU can't effectively cache the contents of a linked list nearly as well as an array resulting in poor performance. This is the main reason why ring buffers are used to implement queues instead of linked lists in high-performance applications where middle insertion and deletion functionality isn't needed (e.g. network drivers).

Time

Linked lists have most of their benefit when it comes to the insertion and deletion of nodes in the list. Unlike the dynamic array, insertion and deletion at any part of the list takes constant time.

However, unlike dynamic arrays, accessing the data in these nodes takes linear time because of the need to search through the entire list via pointers. It's also important to note that there is no way of optimizing search in linked lists. In the array, we could at least keep the array sorted. However, since we don't know how long the linked list is, there is no way of performing a binary search:

\[\begin{array} &&\text{Insertion - O(1),} &\text{Deletion - O(1),} \\ &\text{Indexing - O(n),} &\text{Search - O(n)}.\end{array}\]

Space

Linked lists hold two main pieces of information (the value and pointer) per node. This means that the amount of data stored increases linearly with the number of nodes in the list. Therefore, the space complexity of the linked list is linear:

\[\begin{array} &&\text{Space - O(n)} \end{array}.\]

Example code in Java:

1
2
3
4
5
6
7
8

public class Node{
    public int value;
    public Node next;
    public Node(int v , Node n){
        value = v;
        next = n;
    }
}

The code above describes a node object; these types of objects will usually contain a value (stored in value) and a pointer next which points to another node somewhere in memory. This can be represented as a list with one element in it by writing

1

Node one = new Node(6, null)

Variable one points to a node that contains the value 6. The next field of the cell is null, which could indicate the end of the list. This can be represented as a list with two elements in it by writing

1

Node two = new Node(4, one);

Variable two now points to a cell with a value of 4. The next field of that node points to a node with a value of 6. The next field of the second points to a null object. So, the list is \(4 \rightarrow 6\). A 3 element list is created like this:

1

Node three = new Node(5, two)

Now, it's \(5 \rightarrow 4 \rightarrow 6\).

Note: In this implementation, we have to pass in the pointers to the next node in the list. We do this for simplicity, but usually code has to be written to handle the insertion and deletion of nodes in the list.

It is not necessary for us to create a local variable whenever we need to add a new item to a linked list. A linked list can also be constructed by reading from an array.

1 2 3 4 5 6 7

public static Node createArray(int[] array){ Node list = null; for (int i : array){ list = new Node(i, list) } return list; }

A linked list can be printed either by using recursion or using a loop (iteration). Here is an iterative way of printing a linked list:

1
2
3
4
5
6

public static void printIteratively(Node cell) {
    while (cell != null) {
        System.out.println(cell.value);
        cell = cell.next;
    }
}

We can write the same method recursively:

1
2
3
4
5
6

public static void printRecursively(Node cell) {
    if (cell != null) {
        System.out.println(cell.value);
        printRecursively(cell.next);
    }
}

Write a method that determines the length of a given linked list recursively.

Using our discussed method of iteration, the method can be written as follows:

1 2 3 4 5 6 7

public static void length(Node cell) { int count = 0; while (cell != null){ count += 1; cell = cell.next; } }

Now write a method that determines the length of a linked list recursively.

We can solve this by considering the base case (when P is null) and the recursive case

\[\text{length}(n) = \text{length}(n-1) + 1.\]

1 2 3 4 5

public static int length(Node cell) { if (cell != null) return 1 + length(cell.next); return 0; }

Most methods on linked lists can be implemented both recursively and iteratively. But recursive solutions are more convenient when dealing with linked lists in general. Consider, for example, the following method that takes a linked list as an input and reverses it. For the recursive version, we again identify the base case ( when the list is empty) and the recursive case:

\[ \text{reverse}( Node ) = \text{reverse}(Node.next) + Node.value \]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

Node reverse(Node cell) {
    if (cell == null)
        return null;
    else if(cell.next == null)
        return cell;
    else {
        Node second_segment = reverse(cell.next);
        //cell.next points to the last item in the second segment
        cell.next.next = cell;
        //the next of cell.next now points to cell
        cell.next = null;
        //cell is now the last item in the list
        return second_segment;
    }
}

So far we have only talked about singly linked lists, lists in which pointers go from each cell to the next in one direction. It is however possible to create a doubly linked lists where pointers go both ways.

This allows us to traverse the list in both directions, and it also makes operations such as deletion easier. Because we have pointers to both the nodes before and after the node we'd like to delete, we don't need any more information beyond our target node. In a singly linked list, we also need the pointer to the node we'd like to delete.

Implementation in Java:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

public class DLL {

    private class Node {
        int value;
        Node next, prev;

        Node (E v, Node n, Node p) {
            value=v; next=n; prev=p;
        }

        Node () {     // used only to create header Node in a list
            // that's initially empty
            next=prev=this;
        }
    }

    private Node header = new Node();

    public boolean isEmpty() {
        return header.next == header;
    }

    private E delete(Node p) {
        p.next.prev = p.prev;
        p.prev.next = p.next;
        return p.value;
    }


}

It is now more convenient to traverse the linked list and we can move both backwards and forwards using the prev and next fields, respectively. The design of this type node allows flexibility of storing any data type as the linked list data.

Implement a method to add a node to the end of a linked list:

1 2 3 4 5

public void addLast(int s){ Cell p = new Cell(s , header , header.prev); header.prev.next = p; header.prev = p; }