Magnetic Field Lines
The magnetic field is an abstract entity that describes the influence of magnetic forces in a region. Magnetic field lines are a visual tool used to represent magnetic fields. They describe the direction of the magnetic force on a north monopole at any given position. Because monopoles are not found to exist in nature, we also discuss alternate means to describe the field lines in the sections below. One useful analogy is the close connection between magnetic monopoles and electric charges.

We adopt a few conventions about field lines:
- Since we agree to define the locii in terms of the motion of the north monopole, the field lines enter the south pole and emerge out of the north pole of magnetic dipoles.
- In principle, the field lines can be calculated at every position in space, but this is hard to represent in a visual medium, therefore we use the density of field lines to indicate the field strength.
Contents
Monopoles
Monopoles are (as yet) theoretical objects that have either a north, or a south pole. Another way to imagine these is as magnetic charges, analogous to protons and electrons. Their existence is disputed, although there is some evidence that they can be artificially synthesized. Nevertheless, they are useful tools for thinking about magnetic field lines and to otherwise conceptualize ideas about magnetism. Note that monopoles reduce magnetic phenomena to their electrostatic analogue. We can say that the magnetic field lines emerge out of north poles and converge at south poles.
If monopoles were isolated in nature, they would be found to undergo similar interactions in the electric field as an electric charge undergoes in a magnetic field. For example, the magnetic field of monopoles and the electric field of charges would exhibit the same behavior, and a moving magnetic monopole would induce a circulating electric field (diagram below).

This idea brings us to a different definition for the field lines:
Magnetic field lines:
The magnetic field lines are the trajectories a north magnetic monopole would follow when placed in the magnetic field. \(_\square\)
Whether magnetic monopoles are real or not, the elegance of this idea is evident. One can easily propose a definition of magnetic charge analogous to the electric charge and claim that the field follows a Coulomb-type law
\[B = k \frac{m_1}{r^2}.\]
In fact, employing the Coulomb-style law to model a bar magnet as two magnetic charges of opposite "sign" separated by a short distance faithfully reproduces the shape and variation of the magnetic field strength.
Bar magnet:
Let's begin with the field lines of a bar magnet, perhaps the simplest case to analyze.
- If we released a north monopole near the north pole of the magnet, it would be repelled just like two positive charges placed in close proximity. Thus, we expect a field line emerging from the north pole and heading directly to the left down the \(x\)-axis.
- Above or below the \(x\)-axis, the field lines should start to curl around and head toward the negative pole since north monopoles would be attracted in this direction.
- If we put a north monopole between the \(x\)-coordinates of the north and south pole, we should expect them to travel to the right while curving down to terminate at the south pole.
- Finally, if we place north monopoles far away, but on the right side of the south pole, we should expect them to travel toward the south pole.
Combining this set of insights, we can sketch the field lines of the bar magnet which is done below:

We notice a few things. Close to the bar magnet, the field lines are dense, reflecting the high field strength near poles. As we zoom out from the vicinity of the poles, field lines become less dense, reflecting the diminished field strength. We also see all field lines begin at the north pole and terminate at the south pole. Because the field lines represent the trajectory of particles, they cannot cross; otherwise a particle starting from the point of crossing would have ambiguous dynamics.
At this point, we point out that if we'd pretended the bar magnet was a closely separated pair of electric charges, and calculated their electric field, we would obtain much the same result:

Let us codify our observations from the case of the bar magnet:
Properties of magnetic field lines:
- They are drawn locally as parallel trajectories.
- They never intersect each other (if they do, it means that one pole is pointing in two directions).
- They start from North and terminate at South, outside the magnet, and vice-versa inside. \(_\square\)
Compasses
A compass is a simple device that consists of a permanent magnetic dipole that can rotate freely on top of a pin, and this dipole is called the needle. When placed in a magnetic field, the north pole tends to move in the direction that a north monopole would, and likewise for the south pole. Clearly, this motion is highly constrained and stops once the needle is aligned with the local magnetic field.

The compass is therefore useful to find the local direction of the magnetic field. Since Earth has a simple field with the North pole roughly aligned with true north, the compass is a most reliable tool for navigating the globe. However, if a local magnetic field dwarfs the strength of Earth's magnetic field, the needle will no longer give information about the Earth's field. It can thus be used to map out the magnetic field lines of an electrical device in the lab.

Much like the compass, iron shavings can be used to map out the magnetic field of a device. Each particle in a jar of iron shavings is a small (ferro)magnetic dipole and will align to the local magnetic field. In this way, it is like deploying thousands of tiny compasses all around to get simultaneous global view of the field.
Consider this photograph of iron filings settled around a bar magnet. As you can see, the filings allow us to quite literally see the field.

The Superposition Principle
So far we've considered the magnetic field lines due to a single device. When we want to find out the magnetic field strength due to an object at a particular point, we consider that object only and ignore all other potential field generating objects. This is fine as long as the device under consideration produces a much stronger field than all other nearby sources, or if all other sources are located very far away. However, this will not do if we want to find the magnetic field resultant from several field generating devices of comparable strength located close to one another.
In the case of several devices we carry out the same procedure that we did for a single device and then add them to find the resultant magnetic field at a point. That is, if device \(A\) produces a magnetic field \( \vec{B}_A \) at a point \(x\) and device \(B\) produces a magnetic field \( \vec{B}_B \) at \(x\) then the resultant magnetic field at \(x\) will be \(\vec{B}(x) = \vec{B}_A(x) + \vec{B}_B(x)\). This is known as the principle of superposition.
Two bar magnets:
To generate the field lines for two adjacent dipoles, draw the field lines for each individual bar magnet and then superimpose them. The field lines that are very close to either bar magnet, and far from the other, will be largely the same as they are in the isolated case. This is because the field from the other magnet is weak at far distances and can't significantly distort the local field. In between the two magnets, the story is different. Both fields are of comparable strength in this region and north monopoles will tend to travel from the north pole in the magnet on the right toward the south pole of the magnet on the left. Thus, the field will be more or less horizontal in this region.

In fact, if we simply treat the field lines like vectors, we can see that by vector addition, the field lines between the magnets will attenuate their vertical character and conspire to make largely horizontal field lines pointing from the bar magnet on the right toward the one on the left. Putting all of these insights together, we can sketch the resultant magnetic field for two adjacent bar magnets.

The reader is encouraged to sketch the field line for the following to cases:
- Two bar magnets with adjacent north poles.
- Two parallel bar magnets with opposing poles.
 The diagram above depicts two bar magnets suspended by string. If "N" labels one end of the magnet as magnetic north, then determine the magnetic pole labeled with "?".
The diagram above depicts two bar magnets suspended by string. If "N" labels one end of the magnet as magnetic north, then determine the magnetic pole labeled with "?".
The Right Hand Rule
We now seek to understand how magnetic field lines align around current carrying conductors. To understand the direction of magnetic field lines, we need to be familiar with a mnemonic called the right hand rule. The origins of this rule come from early experiments with iron shavings placed around current carrying wires. The observations are mathematically encoded in one of Maxwell's equations known as Ampere's law.
The right hand screw(grip) rule:
According to this rule, if you place your right hand in "thumbs up" position, with the thumb pointing in the direction that the current is flowing, then the remaining fingers will give you the direction of the magnetic field around the current carrying conductor, illustrated in the figure below. \(_\square\)

Note: The current here refers to the conventional flow (i.e. positive charge), so do not confuse this to be the flow of electrons. The electrons flow in the opposite direction to the conventional flow.

If electrons in a conductor are moving from west to east, in which direction would the magnetic field be produced when looked from the east end?
The electrons are moving from west to east, which means that the conventional flow of current is from east to west. By applying the right hand rule, we come to the conclusion that the direction of the magnetic field is clockwise in a plane perpendicular to the wire, when viewed from east, and anti clockwise when viewed from the west end. \(_\square\)
Field Lines around Conductors
The wire:
A wire is a straight current carrying conductor. It is therefore the most simple system which gives us the simplest type of magnetic field lines with a direct application of the right hand rule. Below is shown a wire flowing current that is coming vertically out of a table. The iron filings on the table show the orientation of the magnetic field around the wire.

As seen in the figure above, the field lines form in concentric circles around the conductor. The strength of the magnetic field around a wire depends on two main things:
- First, the amount of current passing through it. If the current increases, the magnetic field strength also increases (directly proportional): \( B\propto I\).
- Second, the distance from the current carrying conductor. If the distance from the conductor increases the strength of the magnetic field decreases. The magnetic field strength is proportional to the inverse of the distance from the wire: \(B\propto 1/R\).
The current loop:
So far we have discussed the pattern of the magnetic field lines produced in a straight current carrying wire. Let us consider a different situation: let's try bending the same wire into a loop. We find one new thing which we did not see previously: there is a formation of a straight magnetic field line.

As earlier (the wire), the field lines keep expanding, but the loop creates an interaction between the two ends and thus a straight line at the center of the loop. You can apply the right hand rule and verify the direction of the magnetic field. Though the straight magnetic field line is not shown in the figure above, it exists.
Let us verify whether the right hand rule is working in this case. Let's consider the positive terminal. If we keep our hand in thumbs up position we see that the direction of the magnetic field would be anti-clockwise, which is what is shown in the figure. It is exactly the opposite on the negative terminal.
Finally, we verify these arguments by experiments with iron filings:

The solenoid:
A solenoid is a coil of many circular loops wrapped up in the shape of a cylinder. We can find one big similarity between the solenoid and the bar magnet. We find that the magnetic field lines in both cases are exactly the same. In fact, both the ends of the solenoid behave as the poles. One end is the south pole and the other end is the north. This is explained by the clock rule.

The clock rule says that, when electric current enters the solenoid, the direction in which it travels determines the polarity. If it travels a clockwise loop it is South pole, and if it travels an anti-clockwise loop it is a North pole. In this figure, the current is entering in a clockwise direction, so the right end of the solenoid becomes the South pole and the left end is the North pole.
On more important thing to note is that the field lines inside the solenoid are always parallel. This indicates that the magnetic field lines produced inside a solenoid at any point is of the same magnitude, meaning that the field is uniform. Solenoids have wide-ranging applications, and they are mainly used as electromagnets in the metal industries. Another application is in the MRI, where a sloeniod is placed (in super low temperatures) to scan.
Toroid:

The toroid is a hollow circular ring on which a large number of turns of a wire are closely wound. It is like solenoid which is made circular by joining its ends. The magnetic field in a toroid runs in concentric circles of equal magnitude. The field \(B\) inside the toroid is constant in magnitude for the ideal toroid of closely wound turns. The magnetic field outside the toroid is zero. The direction of the magnetic field within a toroid can be easily found by the right hand rule. Grasp the toroid with the fingers of your right hand curled in the direction of the current in the windings. Then the thumb points in the direction of the magnetic field.
Two wires:

When two straight current carrying conductors are kept parallel to each other, they experience some force between each other. The force can be of two types: attraction or repulsion. This force depends on the direction of the current flowing through them. If the current in both the wires is traveling in the same direction, then the two wires attract each other. If the current flowing is in opposite directions, they repel each other.
Applications
The Earth:
You may have read about devastating solar flares caused by solar storms, or about the beautiful ionization patterns that form the Aurora Borealis (Northern Lights). Both these phenomena are related to the magnetic fields of planets and stars. Earth acts much like a bar magnet, with the one obvious difference being size.
To understand this, we need some of the theories that have been proposed to explain this magnetic nature of Earth. In the early \(17^\text{th}\) century, Chinese travelers noticed their compasses being trifled with at sea. Researchers hypothesized that the rotation of Earth and the presence of iron in the mantle of the Earth could cause this anomalous magnetism. These theories were soon refuted and replaced by the geo-dynamo theory, which states that many ions move in the mantle under our Earth's surface, hence creating a current which produces the magnetic field.
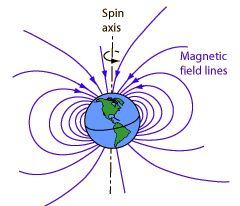
Note, like every bar magnet, our Earth also has two poles, the difference being that these poles do not coincide with our geographic north and south poles, and are therefore known as magnetic poles. From the properties of bar magnets, we know that the magnetic field lines responsible for the field originate at the north and terminate at the south pole, and are thus closed loops. Although Earth is sometimes viewed as having an enormous magnet in its core, that is not at all true, but provides a good picture to the case study.
As mentioned earlier, the magnetic field of Earth deflects harmful solar flares, carrying away ionized particles. Consider a charged particle incoming from the Sun. Headed straight for Earth, it encounters a magnetic field perpendicular to its motion and is deflected away. This creates a protective shield of sorts around the Earth and can sustain typical flares from the Sun. This magnetic shielding effect is illustrated below:

Particle Accelerators:
Particle accelerators are used to ramp elementary particles and atoms up to enormous speeds approaching the speed of light. The particles are then collided and the products of these collisions are carefully analyzed for the signatures of hypothetical or wholly new particles. Accelerators are also used to generate radiation used in cancer treatments such as proton therapy.

Accelerators come in several types, the main variations being the cyclotron and the synchotron.
Cyclotron:
The mechanism of the cyclotron combines a constant magnetic field with a switching electric field to keep particles on spiral paths of ever increasing radius. To see how this works, consider a charged particle of mass \(m\) undergoing circular motion in a constant magnetic field. We of course have the centripetal acceleration of the particle balanced by the Lorentz force upon it:
\[qvB = m\frac{v^2}{r}.\]
This implies \(qB/m = v/r\). As the frequency of the trajectory is given by \(2\pi r/v\), this suggests the frequency of the orbit is just \(1/T = 2\pi m/qB\). We notice that this is independent of the energy or the radius. Thus, a particle of any energy whatsoever will maintain the frequency \(1/T\), even if its energy is changing! We can exploit this incredible regularity of the trajectory (even if it is spiraling) to design a simple accelerator.
Consider a region in which we maintain a constant magnetic field of strength \(B\). Further, consider a dividing line (interface between red and blue in the diagram below). Whenever particles are to the right of this line, the electric field points to the left, accelerating them leftward across the gap, and whenever the particles are on the left, the field points to the right, and they're accelerated rightward. Since the magnetic field keeps the particles in the trajectories at a constant frequency, the particles are regularly accelerated to higher energy each time they cross the gap and they travel on paths of increasing radius.

Considering this in the time domain, we see that we can power this accelerator with an electric field that switches orientation every \(T = qB/2\pi m\) seconds. The black line corresponds to the red-blue interface above.
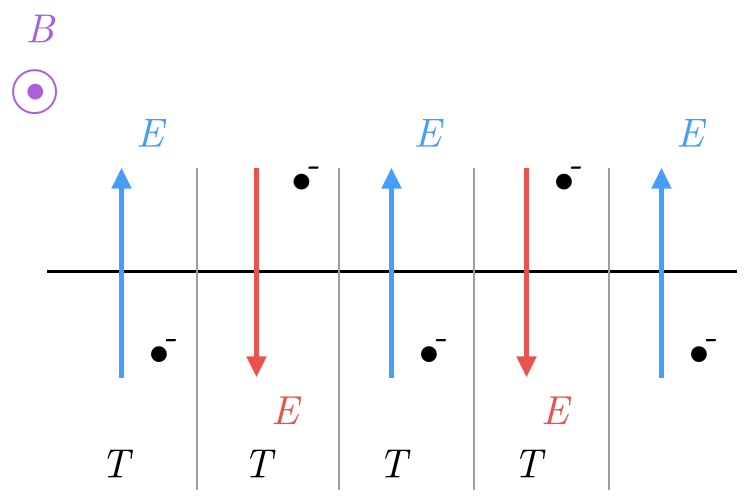
Thus, using a switching \(E\)-field (pointing directly across the gap) and a uniform \(B\)-field (oriented vertically) in tandem, we can accelerate charged particles in spiral trajectories, which can then be released from the accelerator and used for downstream purposes (i.e. collisions, therapy, etc.)
Synchotron:
Synchrotron is an evolved form of cyclotron; it is a type of circular accelerator in which dipole magnets are used to guide the path of the particle and quadrupole magnets are used to keep focused the charged particle beam.
High frequency RF(Radio frequency) field is used to impart the energy to the particles, and the path is kept constant irrespective of energy. The distinction between the cyclotron and the synchrotron is seen due to the production of synchrotron radiation.
Synchrotron radiation occurs when an electron of high energy (speed approaching the speed of light) passes through a dipole magnet, and it experiences a sideways force which causes centripetal acceleration. In this stage, the electron emits intense radiation tangential to its path, known as synchrotron radiation.
The Photon:
Photons of course are the fundamental quanta of light; at a given frequency, the intensity of a light stream can only change in increments of single photon. But photons are also the fundamental quanta of the electromagnetic field. In this view, photons are not just ripples in the EM field, but they are the EM field itself. Thus, an EM wave propagating through space is nothing but a photon.
Suppose we have an oscillating E-field propagating in the \(\hat{x}\)-direction, i.e. \(\vec{E} = A \cos\omega \left(k_xx-wt\right)\hat{x}\). This field is changing in space and time, which means it gives rise to a magnetic field through Faraday's law of induction. The magnetic field is shifted by half a cycle and oscillates perpendicularly to the electric field. Obviously, the argument applies in reverse (a propagating magnetic field gives rise to a perpendicularly oscillating electric field), so that they are inseparable.
Visualizing this result, we see that an EM wave propagating through space consists of coupled \(E\) and \(B\) fields oscillating transverse to a common axis which is the direction of the wave.

The field lines are then arrows pointing from the axis of propagation to the amplitude of each wave.
Feynman's Advice
After all, field lines are just a "crude" way to explain the magnetic field. However, there is more to it than just being a geometrical object. Here' is what Richard Feynman, the pioneer of Quantum Electrodynamics, says in The Feynman Lectures on Physics:
The field lines, however, are only a crude way of describing a field, and it is very difficult to give the correct, quantitative laws directly in terms of field lines. Also, the ideas of the field lines do not contain the deepest principle of electrodynamics, which is the superposition principle. Even though we know how the field lines look for one set of charges and what the field lines look like for another set of charges, we don’t get any idea about what the field line patterns will look like when both sets are present together. From the mathematical standpoint, on the other hand, superposition is easy—we simply add the two vectors. The field lines have some advantage in giving a vivid picture, but they also have some disadvantages. The direct interaction way of thinking has great advantages when thinking of electrical charges at rest, but has great disadvantages when dealing with charges in rapid motion.
He further adds:
The best way is to use the abstract field idea. That it is abstract is unfortunate, but necessary.