Newton's Laws of Motion
Newton's laws of motion are three physical laws that can be considered as the foundation for classical mechanics. They describe the relationship between a body, the forces acting on it, and its motion in response to those forces. Forces are the bread and butter of Newtonian mechanics. Though they're not always the easiest way to think about the world, everything in classical mechanics can be derived from Newton's basic principles that relate force and motion.
Contents
Newton's First Law
The famous statement of the first law is as follows:
Newton's first law states that all objects in motion will remain in motion unless acted on by an external force.
In other words, if there is no force on an object, then its state of motion will not change. Thus, an object that starts at rest will remain at rest, unless it is acted upon by a force. It is perhaps best to illustrate by an example:
Kimmi in a wind tunnel:

Kimmi the skier stands in a wind tunnel to test the airflow of her new outfits. There is a strong wind that pushes her backward with a force of \(200\text{ N}.\) How strong must the frictional force between Kimmi's skis and the floor be in order for Kimmi to stay still?
Because Kimmi doesn't move, we know that \(\Delta v=0\), which implies that the net force on Kimmi \(F_\textrm{net} = 0\).
In other words \(F_\textrm{wind} + F_\textrm{friction} = 0\) and \(F_\textrm{friction} = - F_\textrm{wind}\) so that \(F_\textrm{friction} = -200\textrm{ N}.\)
Net force is the sum of all forces acting on an object:
\[F_\textrm{net} = \sum\limits_i F_i.\]
A corollary to the first law is that if an object is moving, it will keep moving at a constant speed unless acted upon a net force. Mathematically, we say that if \(F_\textrm{net}=0\), then \(\Delta v=0\).
The bench-press:
Imgur
Devin is bench-pressing at the gym. He lifts a barbell of weight \(500\text{ N}\) vertically upward from his chest. If the barbell rises at a constant speed, what is the magnitude of the force Devin exerts on the barbell?
The barbell is acted upon two forces: the downward pull of gravity, and the force with which Devin lifts the barbell up. Since the barbell rises at a constant speed, its state of motion does not change. Thus \(\Delta v=0\), which implies that the net force on the barbell is \(F_\textrm{net}=0\).
In other words, \(F_\textrm{Devin}+500\text{ N}=0\) and \(F_\textrm{Devin}=-500\text{ N},\) so now we know that Devin is pushing the barbell with magnitude \(500\text{ N}\).
Colin and his new laptop:
)
Colin has just bought a new laptop. He places it on his desk and thinks about what he has learned today in science class: "Since this laptop weighs \(3\text{ kg}\), a gravitational force of \(30\text{ N}\) is exerted on it. Then why does it stay on the desk instead of falling to the ground?" Can you answer Colin's question?
Since the laptop stays at rest, \(\Delta v=0\), which implies that the net force exerted on it is zero. As Colin says, a gravitation force pulls the laptop downward with magnitude \(30\text{ N}\). For the net force to be equal to zero, an upward force with magnitude \(30\text{ N}\) must be exerted on the laptop, which is the normal force by the desk.
As we can see from the examples above, objects at rest will stay at rest, and moving objects will continue to move at constant speed if there are no net forces applied. This property of an object, its natural resistance to changes in its state of motion, is called inertia. In fact, another name for the first law is the law of inertia.
Forces
One of the first steps to solving a mechanics problem is the identification of all relevant forces. We say that an object which has some speed \(s\) in a given direction will keep moving at the speed \(s\) in the same direction, unless it is acted upon by an outside influence: a force \(F\). A force is then anything that can cause particles to change their speed, or direction according to an observer who travels at a constant velocity. Forces are perhaps most clearly defined in the statement of the first law:
Newton's first law states that \(\Delta v = 0\) unless acted on by a nonzero force, \(F_\textrm{net} \neq 0.\)
Evidently, a force is something that causes a measurable change in the velocity of an object, according to an inertial observer. Here, we will clearly delineate what we can mean by observer. While it is not necessary, an observer can be thought of as a scientist making a measurement, though in principle there need not be any sentient being, or even any measurement made by an observer in the physics sense of the word.
If a measurement is performed by an observer who moves at a constant velocity, we call the observer an inertial observer. We also say that they sit in an inertial reference frame. Every change in motion that an inertial observer measures is the result of some force acting. Moreover, all inertial observers will agree with one another on the changes in motion that they record.
By contrast, a person sitting on an accelerating train is a non-inertial observer. If a toy car were to be placed on the ground in front of the train, it would appear (to the conductor) to accelerate toward the front of the train. However, the toy car is not actually "moving," but the train is accelerating toward it! This "measurement" is purely a consequence of the observer's own motion, and is not caused by any real force.
Thus, when identifying forces, one must be sure that the frame they're considering is inertial.

Somebody who sits on a train heading due North at the speed \(u\) relative to the ground is an inertial observer. Were they to measure the motion of some object that moves outside the train at constant velocity \(v\) (such as a hummingbird), they would agree with all other inertial observers that \(\Delta v = 0\). The only difference between their measurements and those of other inertial observers could be the hummingbird's absolute velocity.
Newton's laws don't concern velocities as such, but only their change. From the perspective of an inertial observer, acceleration is the sign of an underlying force. There are no illusory accelerations seen by inertial observers due to their own motion. Whenever we observe an accelerating object in an inertial reference frame, we can find the force that causes it.
Concretely, if somebody on the train measured the speed of a hummingbird flying at speed \(v\) relative to the ground, the observer on the train would measure the hummingbird's speed as \(v^\prime = v - u\), while the observer on the ground would measure \(v\). In general, \(v_\textrm{hummingbird} \neq v_\textrm{hummingbird}^\prime\), as measured by two inertial observers. There are no perceived accelerations that can arise purely because of the observer's own motion.
Let's look at some examples:
Airbus takeoff:

During takeoff, a passenger jet accelerates from zero to takeoff speed so that \(\Delta v=v_\textrm{takeoff}\). What causes this acceleration?
The acceleration of the Airbus is caused by the force of thrust from the engines. The engines accelerate the air molecules, blasting air backward at very high speed. Because forces balance, the plane is pushed forward with the same force.
Jimmy's 3-pointer:
Imgur
Jimmy is playing guard in a basketball tournament. He makes a shot and scores 3 points. During his shot the ball leaves his hands, goes up in the air, and falls back into the net. If the air resistance is negligible, what causes the ball to descend?
After the ball leaves Jimmy's hands, it experiences one force: the downward pull of gravity. This causes a downward acceleration of \(g\approx10\text{ m/s}^2\), so the ball slows down while ascending, then falls back down. The ball's horizontal motion does not change during its flight, since there is no force acting horizontally on the ball.
Kimmi on the slope:

Kimmi now goes on the slope to test the actual performance of her outfits. She starts at the top of the slope, and gains speed. After gaining a speed of \(20\) miles per hour, she slides down at a steady rate. Then she applies her brakes and comes to a complete stop. Explain the relationship of the forces during her descent.
The force pulling her down the slope, which is the downward pull of gravity, is the source of her acceleration. During her acceleration this gravitational force is larger than the sum of the force due to air resistance, and the friction force between her skis and the slope.
When she slides down at a steady \(20\) miles per hour, \(\Delta v=0\), which means the net force is equal to zero. Thus the gravitational force and the sum of the force exerted by air resistance and friction force are equal in magnitude. When she applies her brakes, the sum of friction force and air resistance becomes larger than the gravitational force and lets her slow down to stop.
We can manifest these relationships between the forces as follows:
\[\begin{array}{rrl} (1) &\text{Acceleration phase: }&\lvert F_\textrm{gravity}\rvert>\lvert F_\textrm{air}+F_\textrm{friction}\rvert \\ (2) &\text{Uniform motion phase: }&\lvert F_\textrm{gravity}\rvert=\lvert F_\textrm{air}+F_\textrm{friction}\rvert \\ (3) &\text{Deceleration phase: }&\lvert F_\textrm{gravity}\rvert<\lvert F_\textrm{air}+F_\textrm{friction}\rvert. \end{array}\]
Car skidding:
When a car skids to a stop at a traffic light, the road pulls on the car through the rubber wheels and its velocity decreases in magnitude. The car is acted on by a force of friction.
There are lots of examples in ball sports.

Hitting a baseball:
When a player hits a baseball with a bat, the bat pushes on the ball and the speed of the ball is initially decreased. Then the direction of the ball's motion is reversed, and the ball accelerates again in the opposite direction. The ball is acted on by the force of contact.
There are even better examples in other sports

Skateboard ollie:
A skater lifts off the ground by kicking a skateboard against the ground with a force \(F_\textrm{kick}\), propelling them off the ground with velocity \(v\). Once they're in the air, they immediately start losing speed until the top of their jump, then \(v=0\). After the peak they accelerate back toward the ground.
Non-inertial Observers
If motion is measured by an observer who is accelerating, they are a non-inertial observer, and they can observe motions which appear to be the result of forces acting, but are really just artifacts of their own motion.

A skydiver accelerating toward Earth is not an inertial observer. Were the skydiver to measure the speed of an elephant who is sitting still on the Earth's surface, they would perceive the elephant as accelerating toward them with \(a_\textrm{elephant} = g\), and would think that the elephant was acted upon by a net force.
However, no observer from another reference frame would agree with them about the value of \(a_\textrm{elephant}\) that they assign to the elephant (indeed it is zero!), i.e. their measurement of \(a_\textrm{elephant}\) is frame dependent.
For this reason, Felix Baumgartner was not an inertial observer during his free-fall from space.
Puck on an accelerating ice rink:
An example of an acceleration with no associated force is a hockey puck sitting on a sheet of ice in the back of a pickup truck, that appears to accelerate toward the back of the truck from the perspective of a passenger. The puck's acceleration is not real, but an illusion which arises from the fact that the passenger sits in an accelerating frame of reference (the truck), not a force.
Change is the Difference
It is okay for velocity measurements to be frame dependent because Newton's laws don't care about the absolute value of velocity, but only changes in it. Acceleration on the other hand is central to the laws of motion. We care deeply about the absolute value of the acceleration, not only in its changes.
Newton's Second Law
As stated in the first law, a force \(F\) can give rise to the acceleration \(a\) of massive objects, so we expect a relationship between them, perhaps something direct like \(F \propto a\) (which denotes that \(F\) and \(a\) are proportional to one another).
But, do we expect a force \(F\) to accelerate any massive object with the same \(a\)? The answer is no.
Based upon common sense, we expect things that weigh less to accelerate more quickly than objects which weigh more, when we apply the same force \(F\).

Same force, different effect:
Think of what would happen if we use the jet engine of a plane to propel a cruise ship. Although we're providing a lot of thrust, we don't expect the ship to accelerate very quickly because of how heavy it is.
Now, think of using the jet engine to propel a waiter to your table... actually, you can just watch:
Our observation suggests that the factor of proportionality in \(F \propto a\) is \(m\), the mass of an object. In other words: \(F/m = a\), the more mass an object has, the less it will accelerate under a given force \(F\). Thus the second law can be summarized with one simple equation:
Newton's second law:
\[F=ma.\]

A \( 500 \text{-kg} \) rocket is to be accelerated from rest to \( 1600 \text{ km/h} \) at a constant rate in \( 1.8 \) seconds. What is the approximate magnitude of the required net force?
Assume the loss of fuel makes a negligible change to the mass of the rocket.

Surfer tow-in:
A \(150 \text{ kg}\) surfer is towed in to a wave by a jet-ski with a rope of tension 30 N. At the same time, they feel a drag force of 10 N from the friction with ocean water. How quickly does the surfer accelerate while being towed in to the wave?
Because the pull of the jet-ski and the drag force act in opposite directions, the surfer feels a net force of \(30\text{ N} - 10\text{ N} = 20\text{ N}\) toward the wave. Applying the second law, we find the surfer's acceleration
\[a_\textrm{surfer} = \frac{F}{m} = \frac{20\textrm{ N}}{150\textrm{ kg}} = 0.13\bar{3}\textrm{ m/s}^2.\]
Derivation of Newton's first law from the second law:
From the second law, we have \(F=ma.\)
If no force acts on the body, then \(F=0.\)Then, \(0=m\left(\frac{v-u}{t}\right),\) i.e. \[0 \times t=m(v-u) \implies 0=mv-mu \implies mv=mu.\] Finally, cancelling \(m\) from both sides, we have \(v=u.\)
Hence, if no unbalanced external force \((F=0)\) acts on a body, it will remain in rest or in uniform motion \((v=u).\)
What is mass anyways? When you first learn about mass, it's often introduced as the coefficient that relates the force applied to an object to how the object accelerates. In short, we have the definition of the inertial mass as \[m=\frac{\big|\vec{F}\big|}{|\vec{a}|}\] from Newton's second law. Some objects, like electrons and protons, have masses while other objects, like photons, don't. This series of problems will walk you through how one can generate mass for different particles by the Higgs mechanism, which you may have heard of since it has been in the news a lot in the last few years (and is one of the major motivations for the Large Hadron Collider in Europe).
We start with a (hopefully) simple question: Which of the following statements is correct in Newtonian mechanics?
A Circle to Start
If we inspect the definitions for force, and mass, they seem a bit circular.
For example, we have the following two definition for mass and force:
1) A force is something that accelerates an object of mass \(m\) according to \(F/m=a.\)
2) An object has mass \(m\) if it accelerates at the rate \(\displaystyle a = F/m\) under the force \(F.\)
However, these definitions provide a practical means to compare the behavior of objects under different influences, and we can use this to build up a deep theory of the motion of matter. After all, theories in physics only matter insofar as they agree with experiments: all models must makes themselves vulnerable to experimental verification. Consequently, all models must start with some unprovable assumptions.
Airbus reloaded:

During takeoff, a passenger jet accelerates from zero to takeoff speed by pulling air molecules through the engine at the speed \(v_\textrm{air}\). What is the magnitude of the plane's acceleration?
The acceleration of the Airbus is caused by the thrust from the engines. The engines pull air through them and accelerate the air molecules to very high speeds. As forces are balanced, the plane is pushed forward with the same force.
A volume of air has a mass given by \(M_\textrm{air} = \rho_\textrm{air} V_\textrm{air}\), and the engine accelerates it backward at speed \(v_\textrm{air}\).
If the engine has cross-sectional area \(A_\textrm{engine}\), then the engine accelerates a mass \(\rho_\textrm{air}A_\textrm{engine}v_\textrm{air}\Delta t\) kg of air in the time \(\Delta t\) it takes to accelerate across the engine.
Because the air picks up \(\Delta v \approx v_\textrm{air}\) in time \(\approx \Delta t\), we can estimate its acceleration through the engine to be \(a_\textrm{air} \approx v_\textrm{air}/\Delta t\).
Thus, the plane accelerates forward with
\[\displaystyle \begin{align}a_\textrm{plane} &\approx \frac{M_\textrm{air}}{M_\textrm{plane}}a_\textrm{air} \\ &= \frac{\rho_\textrm{air}}{M_\textrm{plane}}A_\textrm{engine}v_\textrm{air}\Delta t\frac{ v_\textrm{air}}{\Delta t} \\ &= \frac{\rho_\textrm{air}}{M_\textrm{plane}}A_\textrm{engine}v^2_\textrm{air}.\end{align}\]
Identifying Interactions between Objects
Newton's third law of motion states that there are no unbalanced forces in a closed system, which is equivalent to the famous parable:
For every action, there is an equal and opposite reaction.
This means that whenever we find a force from one object A acting upon another B, there exists another force, equal in magnitude, from B to A.
Box on the ground:
Resting on the ground, an object weighing \( \frac{1}{g}\text{ kg}\) presses on the Earth with force \(1 \text{ N}.\) In turn, the Earth pushes back up with \(1 \text{ N}.\)
Force pairs do not get much more involved than this, though the story is usually complicated by convenient simplifications.
1. Near infinite mass
One is to treat extremely massive objects as effectively immovable. For example, it may seem that an object in freefall toward a giant mass, like the Earth, is being acted on by the gravity of the Earth, but that the reverse action is not. In reality, the object is acting on the Earth with exactly the same force. However, because the mass of the Earth is so big next to the mass of the object, the effect on the motion of Earth is indiscernible.2. Fields
Another potential source of confusion are fields. Whenever a force is transmitted over a distance, it can be useful to form a field. For instance, above the Earth, it is common to represent the force gravity as a field of strength \(G\frac{M_\textrm{Earth}}{R_\textrm{Earth}^2}\). Because changes in height are usually small relative to the Earth's radius \(R_\textrm{Earth}\), the field strength is approximately constant, and the force felt by any mass is just its mass \(m\) times the acceleration due to gravity \(\approx g\). In this picture, it may seem like the force comes from the field to the object, and that the object isn't actually interacting with the Earth. However, the field is just a convenient way to simplify calculations. In truth, the object has its own field whose strength is too weak to cause any appreciable acceleration of the Earth, so it is swept under the rug.
Newton's Third Law
Newton's third law of motion expresses a simple fact about forces: they describe the interaction of things. In other words, a force cannot be exerted on nothing. What does this imply for the forces between interacting objects?
Two objects floating in free space:
The forces that describe the interaction of two objects must be perfectly balanced by one another. If they weren't, the two objects considered together would have a net force left over which acts upon nothing.
This implies that whenever object A pushes on object B with force \(F_{AB}\), object B pushes back with \(F_{BA} = -F_{AB},\) and that therefore
\[\sum F = F_{AB}+F_{BA}=0.\]
The two forces are equal in magnitude, but point in opposite direction.
In practical terms, this means that if I push on something, it will push back on me.
Isaac Newton's pro skater:

If a skateboarder wants to jump off the ground, they have to push their board down on the solid ground. In return, the solid ground pushes up on them with an equal force, causing them to lift off the ground.
Nothing significant happens to the Earth because it is so much heavier than the skateboarder \(\left(M_E \gg m_\textrm{skater}\right),\) but if we were to look very, very closely, we'd see that the Earth actually moves by a tiny distance when the skateboarder leaves the ground.
Rocket power:

Partnering the Earth with an ordinary object in a balance of forces is a little extreme. The Earth has so much more mass than any common objects that its acceleration is virtually unnoticeable to the senses.
The force balance is apparent in more equal pairings. For example, if someone sit on a cart and spray a fire extinguisher to the left (accelerating the foam molecules to the left), they will roll to the right.
Seriously, watch it:
Like the rest of the examples, the fire extinguisher cart can be understood as a consequence of the third law.
Can you explain it?
How much momentum will a dumb-bell of mass \(10\text{ kg}\) transfer to the floor, if it falls from a height of \(80\text{ cm}\)? Take its downward acceleration to be \(10 \textrm{ m/s}^2\).
We have
\[\begin{align} \text {Mass of the body (m)} & = 10\text{ kg}\\ \text {Height(h)} & = 80\text{ cm} = 0.8\text{ m}\\ \text {Acceleration (a)}&= 10 \textrm{ m/s}^2\\ \text {Initial velocity (u)} &= 0 \text{ m/s}\\ \text {Final velocity (v)} &=\, ? \end{align}\]
Applying \(v^2 - u^2 = 2ah\) gives
\[\begin{align} {(v)}^2 - {(0)}^2 & = 2 × 10 × 0.8\\ v^2 & = 16\\ v & = \sqrt{16} = 4\text{ (m/s)}. \end{align}\]
Therefore,
\[\begin{align} \text {Momentum of dumb-bell before hitting ground (P)} & = m × v\\ & = 10 × 4 \\ &= 40 \text { (kg m/s)}. \end{align}\]
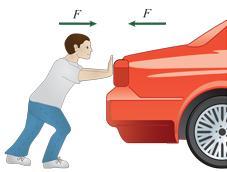
You push a heavy car by hand. The car, in turn, pushes back on you. Doesn't this mean that the forces cancel each other, making acceleration impossible?
Why or why not?
A. Yes: In accord with Newton's second law, \(a =\frac{F_\text{net}}{m}\), and since \(F_{net}=F_{you}+F_{car}=0\), no acceleration occurs.
B. Yes: In accord with Newton's first and third laws, an object continues in its state of rest unless it is compelled to change that state by forces impressed upon it. Since the net force is zero, the car doesn't move.
C. No: In accord with Newton's third law, I push the car and the car pushes with an equal and opposite force on me. Thus, with Newton's second law and \(a=\frac{F}{m}\), the car accelerates, but so do I in an equal and opposite direction.
D. No: An external, horizontal force is applied to the car by my push; the car accelerates (in accord with Newton's first law).
\(\)
Note: By acceleration we mean acceleration relative to the ground.
Problem credit: Conceptual Physics: Special Edition Series, Paul G. Hewitt