Nim
Nim is a combinatorial game, where two players alternately take turns in taking objects from several heaps. The only rule is that each player must take at least one object on their turn, but they may take more than one object in a single turn, as long as they all come from the same heap.
Nim is the most well-known example of an impartial game, a game where both players have the same moves all the time, and thus the only distinguishing feature is that one player goes first. It is also completely solved, in the sense that the exact strategy has been found for any starting configuration.
Contents
Rules
The basic Nim begins with two players and several heaps, each containing several objects. Occasionally, heaps are also called piles, and the objects are called stones.
Each player, in turn, must take at least one stone, but they may take more than one stone as long as they all come from the same pile. It's allowed to make a pile empty, effectively removing the pile out of the game. When a player is unable to move, the game ends. Naturally, as long as there is a stone, either player can take that stone, and thus can move. So the ending condition can be rephrased, where the game ends if there is no stone left.
In normal Nim, the loser is the player unable to move. It is called normal condition by convention from combinatorial game theory, where a normal game gives the win to the last player making a move. In misère Nim, the player unable to move wins instead; this is equivalent to the player taking the last stone losing.
Example Game
Consider the following example of the game. There are three piles, initially having \(3, 4, 5\) stones respectively. Alice and Bob are playing, with Alice starting.
| Pile 1 | Pile 2 | Pile 3 | Move |
| \(3\) | \(4\) | \(5\) | Starting position |
| \(1\) | \(4\) | \(5\) | 1. Alice takes \(2\) stones from Pile 1 |
| \(1\) | \(4\) | \(3\) | 2. Bob takes \(2\) stones from Pile 3 |
| \(1\) | \(2\) | \(3\) | 3. Alice takes \(2\) stones from Pile 2 |
| \(0\) | \(2\) | \(3\) | 4. Bob takes \(1\) stone from Pile 1 |
| \(0\) | \(2\) | \(2\) | 5. Alice takes \(1\) stone from Pile 3 |
| \(0\) | \(1\) | \(2\) | 6. Bob takes \(1\) stone from Pile 2 |
| \(0\) | \(1\) | \(1\) | 7. Alice takes \(1\) stone from Pile 3 |
| \(0\) | \(1\) | \(0\) | 8. Bob takes \(1\) stone from Pile 3 |
| \(0\) | \(0\) | \(0\) | 9. Alice takes \(1\) stone from Pile 2 |
In normal play, Alice wins, as Alice has taken the last stone and thus leaving Bob with no move. In misère play, Alice would lose instead, but in this case Alice would have taken \(2\) stones from Pile 3 on move 7, leaving Bob with pile sizes \(0, 1, 0\) and thus forcing Bob to take the last object.
In the above game, Alice has played a perfect game, never letting Bob to be able to snatch the win. This can be generalized into a general strategy.
Strategy
The nim-sum \(a \oplus b\) of two non-negative integers \(a\) and \(b\) is defined as follows. Represent \(a\) and \(b\) as sums of distinct powers of two. Cancel powers of two appearing twice, and add up the remaining numbers. Nim-sum is also known as XOR by computer scientists.
For example, \(3 \oplus 5\) can be computed as follows. We have \(3 = 2^1 + 2^0\) and \(5 = 2^2 + 2^0\). We cancel \(2^0\) for appearing twice, and add up the remaining \(2^1 + 2^2\), giving \(3 \oplus 5 = 6\).
It can be shown that \(\oplus\) is associative, thus making the nim-sum of several numbers \(a_1 \oplus a_2 \oplus \ldots \oplus a_n\) defined.
Now, given a normal Nim position (the sizes of the piles) \(a_1, a_2, \ldots, a_n\), the player to move wins if \(a_1 \oplus a_2 \oplus \ldots \oplus a_n \neq 0\); a winning move can be found by determining a pile \(i \in \{1, 2, \ldots, n\}\) and a number \(b_i \in \{0, 1, \ldots, a_i - 1\}\) such that \(a_1 \oplus a_2 \oplus \ldots \oplus a_{i-1} \oplus b_i \oplus a_{i+1} \oplus a_{i+2} \oplus \ldots \oplus a_n = 0\), and taking some stones from pile \(i\) such that \(b_i\) stones are left. If \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\), then the player to move loses.
For example, in the above game with \(3, 4, 5\), we see that \(3 \oplus 4 \oplus 5 = 7 \oplus 5 = 2\), and \(1 \oplus 4 \oplus 5 = 5 \oplus 5 = 0\), so the player to move (in this case Alice) wins by reducing the first pile from \(3\) stones to \(1\) stone. After that, \(1 \oplus 4 \oplus 5 = 0\), so theoretically the player to move (in this case Bob) loses, as long as the opponent plays perfectly.
In misère Nim, the strategy is almost identical. As long as after the suggested move, there will be at least one pile of size \(2\) or larger, follow the strategy of the normal Nim. However, if after the suggested move, there will be no pile of size \(2\) or larger, play a different move:
- If the suggested move makes the pile have \(1\) stone left, make it have \(0\) stones instead, or
- If the suggested move makes the pile have \(0\) stones left, make it have \(1\) stone instead.
In other words, the correct move is to leave an odd number of piles of size \(1\). (In normal play, there should be an even number of piles of size \(1\) instead, to make the nim-sum zero.)
Proof of Winning Strategy
The following proof is for normal Nim's strategy, given by C. Bouton.
The moving player wins in normal Nim if and only if the nim-sum of the pile sizes is not zero.
We will begin with the easy base case: if the pile sizes are all zero, then the moving player loses and the nim-sum is zero. From now on, assume that not all pile sizes are zero.
First, we observe that the nim-sum obeys the following several properties for all non-negative integers \(a,b,c:\)
- Associativity: \((a \oplus b) \oplus c = a \oplus (b \oplus c)\)
- Commutativity: \(a \oplus b = b \oplus a\)
- Identity: \(0 \oplus a = a\)
- Self-inverse: \(a \oplus a = 0\)
- Computing nim-sum of multiple numbers at once is possible: write all numbers as sums of distinct powers of 2, find all powers of 2 that appear an odd number of times, and sum up one occurrence of each power of 2. For example, \(1 \oplus 3 \oplus 7 = \big(2^0\big) \oplus \big(2^0 + 2^1\big) \oplus \big(2^0 + 2^1 + 2^2\big) = 2^0 + 2^2 = 5\).
Suppose the pile sizes are \(a_1, a_2, \ldots, a_n\) before a move, and \(b_1, b_2, \ldots, b_n\) after a move. Suppose that the move is on pile \(k\); then for all \(i \neq k\), \(a_i = b_i\). Let \(s = a_1 \oplus a_2 \oplus \ldots \oplus a_n\) and \(t = b_1 \oplus b_2 \oplus \ldots \oplus b_n\). We have
\[\begin{align*} t &= 0 \oplus t \\ &= (s \oplus s) \oplus t \\ &= s \oplus (s \oplus t) \\ &= s \oplus \big((a_1 \oplus a_2 \oplus \ldots \oplus a_n) \oplus (b_1 \oplus b_2 \oplus \ldots \oplus b_n)\big) \\ &= s \oplus \big((a_1 \oplus b_1) \oplus (a_2 \oplus b_2) \oplus \ldots \oplus (a_n \oplus b_n)\big) \\ &= s \oplus \big(0 \oplus 0 \oplus \ldots \oplus 0 \oplus (a_k\oplus b_k) \oplus 0 \oplus \ldots \oplus 0\big) \\ &= s \oplus (a_k \oplus b_k). \end{align*}\]
Now we will prove two results.
Result 1: If \(s = 0\), then \(t \neq 0\). If the nim-sum of the original sizes is zero, then the moving player is losing (they must make the nim-sum nonzero).
We claim that \(a_k\oplus b_k \neq 0\). Indeed, suppose it is, then
\[\begin{align*} a_k &= a_k \oplus 0 \\ &= a_k \oplus (a_k \oplus b_k) \\ &= (a_k \oplus a_k) \oplus b_k \\ &= b_k. \end{align*}\]
Thus \(a_k = b_k\). But this contradicts the fact that the moving player moved on pile \(b_k\), and thus must make the size different.
Thus, since \(a_k \oplus b_k \neq 0\), we have
\[\begin{align*} t &= s \oplus (a_k \oplus b_k) \\ &= 0 \oplus (a_k \oplus b_k) \\ &= a_k \oplus b_k \\ &\neq 0. \end{align*}\]
Result 2: If \(s \neq 0\), it's possible to make \(t = 0\). If the nim-sum of the original sizes is not zero, the moving player is winning (they can make the nim-sum zero).
Consider the largest power of 2, \(2^k\), not greater than \(s\). There must be at least one \(a_i\) such that it also contains \(2^k\), otherwise \(2^k\) cannot appear in \(s\). Now, take \(b_i = s \oplus a_i\). The value \(b_i\) decreases by \(2^k\), and increases by at most \(2^{k-1} + 2^{k-2} + \cdots + 2^0 = 2^k - 1\) (each remaining powers of 2 making up \(s\) adds to the value; for example \(s = 2^2 + 2^1 + 2^0\) and \(a_i = 2^3 + 2^2\) gives \(b_i = 2^3 + 2^1 + 2^0\)), so \(b_i < a_i\). Moreover,
\[\begin{align*} t &= s \oplus (a_i \oplus b_i) \\ &= s \oplus \big(a_i \oplus (s \oplus a_i)\big) \\ &= (s \oplus s) \oplus (a_i \oplus a_i) \\ &= 0. \end{align*}\]
This proves the theorem. \(_\square\)
The strategy given above for misère Nim is correct: follow normal Nim strategy, except that when the moving player is going to make all pile sizes less than \(2\) stones, the moving player makes the number of piles of \(1\) stone odd instead of even.
The only change is when the moving player needs to reduce the single pile having size \(2\) or more to less than \(2\) \((\)other piles have sizes no more than \(1).\)
Suppose the piles are \(a_1, a_2, \ldots, a_n\), where \(a_1 \ge 2\) and \(a_2, a_3, \ldots, a_n \le 1\). Then \(a_2 \oplus a_3 \oplus \ldots \oplus a_n = 0 \vee 1\). If \(a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0\), this would imply \(a_1 = 0 \vee 1\), contradiction. So the moving player is winning. It's also clear that the moving player can make the first pile to have only zero or one stone, since it begins with at least \(2\) stones.
Once the moving player decides the move, the rest of the game is forced; with an odd number of \(1\)-sized piles and the opponent starting, the opponent will also take the last stone, thus losing.
This proves the correctness. \(_\square\)
Other Variations of Nim
There are many variations of Nim. The most well-known ones are normal Nim and misère Nim; in several textbooks, normal Nim is considered to be the standard game and misère Nim is the variant, while in others, it's the other way around. Due to Nim being a very basic game, there are so many possible variants obtained by simply adding one extra rule; this list doesn't intend to cover all possibilities, only the well-known ones.
A variant is known as subtraction game. This is equivalent to Nim, but where the number of stones taken is limited to some set of positive integers: for example, the first \(k\) numbers or the square numbers. Generally, this is played with one pile only.
Usually, Nim is played with the stones clumped together in heaps. A variant places the stones in rows so that taking stones in the middle of a row breaks the row into two. In other words, a player's move is to take at least one stone from a pile and optionally split the pile into two piles. Kayles is played with a single pile, allowing splitting, but a player may take at most \(2\) stones at a time. Dawson's chess is another variant of Kayles, where a player may take at most \(3\) stones at a time; however, taking one stone is only allowed if it's the only stone in a pile, and taking two stones doesn't allow splitting. Circular Nim is played with stones initially arranged in a circle, so the first time the pile is played on, it cannot be split; additionally, one can only take no more than \(3\) stones.
A generalization of Nim is the octal game. Players take turns removing several stones from a single heap in each turn, just as in usual Nim; however, the rules that govern when and how a heap can be taken and/or split are compactly noted as an octal number. For the octal game \(\overline{0.d_1 d_2 d_3 d_4 \ldots}\), the digit \(d_n\) specifies how many heaps are allowed to be left after removing \(n\) stones from a heap. \(d_n\) is the sum of
- \(1 = 2^0\) if leaving \(0\) heaps is permitted (the heap has exactly \(n\) stones), \(0\) otherwise;
- \(2 = 2^1\) if leaving \(1\) heap is permitted (the heap has more than \(n\) stones), \(0\) otherwise;
- \(4 = 2^2\) if leaving \(2\) heaps is permitted (take \(n\) stones from the heap and split the rest into two non-empty heaps), \(0\) otherwise.
As an example, Dawson's chess has the octal game notation \(0.137\):
- Removing \(1\) stone is only possible when it's the only stone in the pile, so \(d_1 = 1+0+0\).
- Removing \(2\) stones is possible at any time, but it doesn't allow splitting the pile, so \(d_2 = 1+2+0\).
- Removing \(3\) stones is possible at any time, including splitting the pile, so \(d_3 = 1+2+4\).
The regular Nim has octal game notation \(0.3333 \ldots\). Kayles has octal game notation \(0.77\).
Octal games have further variants. The first digit, corresponding to removing \(0\) stones, may be set into \(4\) to indicate that splitting a heap into two (without taking any stones) is a permitted move. By using a higher base, it's possible to express games that allow splitting a heap into three or more heaps.
Index-\(k\) Nim is a variant of Nim where a player is allowed to take stones from more than one pile in a single turn. This can be combined with subtraction game, limiting the total number of stones removed or the number of stones removed from a pile.
Wythoff's game is a variant of Index-\(k\) Nim, where the number of stones removed from all piles affected must be the same. Usually, Wythoff's game is played with only two piles. The strategy is very different; the two-pile game is solved, involving Beatty's sequences using \(\varphi\) and \(\varphi^2\).
Grundy's game is even more different in that stones cannot be taken. The only allowed move is to split a pile into two differently sized piles. This will still end the game since the number of piles will be limited by the number of stones and it keeps increasing.
Unbalanced Nim has the extra rule that any two heaps may not be equal in size. Heaps of zero objects may or may not be counted as heaps; in the former option, this makes the ending position different, as \(0, 1, 2, \ldots, n-1,\) where \(n\) is the number of heaps.
Even more quirky variants are greedy Nim, where a player may only take stones from the currently largest pile—any such largest pile if there are many—and building Nim, where the players begin with placing \(n\) stones into \(p\) piles before playing a game of Nim with the result, so that the starting position is not known until the end of the building phase.
Nimbers and Sprague-Grundy Theorem
The Sprague-Grundy theorem is more fully developed out on this page.
The Sprague-Grundy theorem
Any position of an impartial game is equivalent to a Nim pile of a certain size.
Nim Problems
 Two players play a game according to the following rules:
Two players play a game according to the following rules:
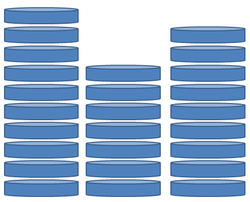
They place three heaps of coins on a table. The first heap has \(10\) coins, the second heap has \(7\) coins, and the third heap has \(9\) coins.
The second player adds another pile of coins on the table, having at most \(10\) coins.
The players take turns alternately, starting with the first player. At each move, the player has to remove a positive number of coins from one heap. The player who removes the last coin wins.
It turns out that regardless of the strategy of the first player, the second player always wins with optimal play. How many coins should the second player add in the fourth pile?
Dan and Sam play a game on a \(5\times5\times5\) cube that consists of 125 objects; each one must take at least one object and at most a whole heap, in his turn.
As an explicit example, in the first turn, Dan can take just the bottom front left corner object, or the whole vertical central heap, or the whole bottom front horizontal heap. Thus, he can take any number of objects of one of the 125 initial heaps (heaps cannot be diagonals).
The winner is the one who takes the last object. If Dan begins, who will win? This means, who has a winning strategy?

This is the fifteenth problem of the set Winning Strategies.
Dan and Sam play a game on a \(4\times9\) grid, in which one takes squares (red) and the other takes circles (blue). Once the game starts, they take turns moving a single piece in their turn. Each piece can only be moved straight forward or backward, any number of grids (and cannot skip over the opponent's piece). This is the initial position:

A player loses when he is not able to move any of his pieces in his turn. If Dan goes first, who will win? In other words, who has a winning strategy?
This is the twelfth problem of the set Winning Strategies.
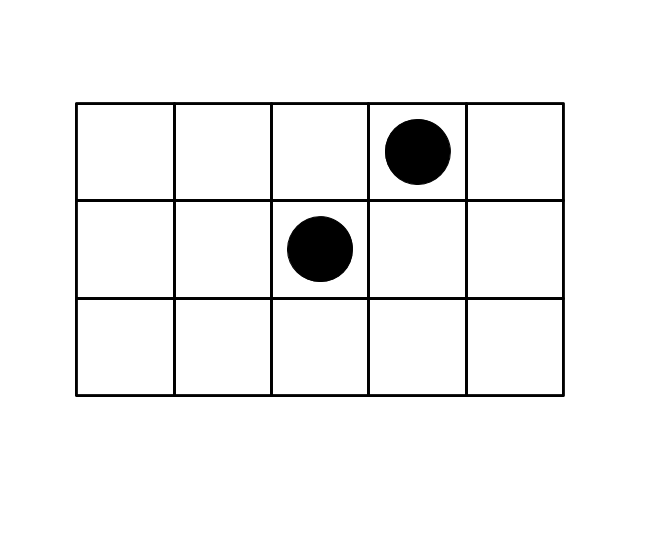
Alice and Bob are playing a game called Moving Chips. The game is played on an \(n \times m\) board where some cells have some chips on it. Two players move alternately. Each turn consists of one person moving a chip to any cell to its left or any cell to its top. For example, the possible movements of chip A on a \(3\times 5\) board are as follows:

The last player who moves all the chips to the top left cell wins.
Consider the configuration below. Alice will move first. Assuming that both players move optimally, who will win the game?
Clarification:
The chips can be stacked on top of one another.
The chips can move past any chips.
Do you have a generalized strategy for this problem? Then you might enjoy the Large Data version!