Normal Distribution
The normal distribution, also called the Gaussian distribution, is a probability distribution commonly used to model phenomena such as physical characteristics (e.g. height, weight, etc.) and test scores. Due to its shape, it is often referred to as the bell curve:
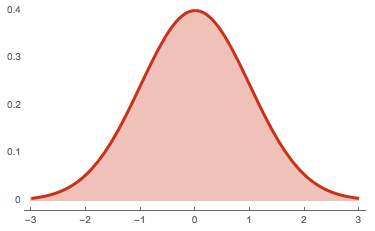 The graph of a normal distribution with mean of \(0\) and standard deviation of \(1\)
The graph of a normal distribution with mean of \(0\) and standard deviation of \(1\)
Owing largely to the central limit theorem, the normal distributions is an appropriate approximation even when the underlying distribution is known to be not normal. This is convenient because the normal distribution is easy to obtain estimates with; the empirical rule states that 68% of the data modeled by a normal distribution falls within 1 standard deviation of the mean, 95% within 2 standard deviations, and 99.7% within 3 standard deviations. For obvious reasons, the empirical rule is also occasionally known as the 68-95-99.7 rule.
In addition, the normal distribution exhibits a number of nice simplifying characteristics, many of which may be observed from the above plot. It is symmetric and single-peaked, implying that its mean, median, and mode are all equal. It additionally has "skinny tails", intuitively meaning it "tapers off" quickly and formally means it has a kurtosis of 0.
Contents
Normality and the Central Limit Theorem
Many physical phenomena, like height and weight, closely follow a normal distribution. This is somewhat counterintuitive on first glance since normal distributions are positive everywhere but it is clearly impossible to have a negative height, but normal distributions have skinny enough tails that these probabilities are negligible.
Intuitively, the normal distribution is "nice" enough that we expect it to occur naturally unless there is a good reason to believe otherwise. This intuition is formalized by the central limit theorem, which states the following:
The probability distribution of the average of \(n\) independent, identically distributed (iid) random variables converges to the normal distribution for large \(n.\)
In fact, \(n = 30\) is typically enough to observe convergence. Intuitively, this means that characteristics that can be represented as combinations of independent factors are well-represented by a normal distribution. For instance, if we flip a coin many times, the number of heads can be viewed as the sum of many iid random variables and thus would be well-represented by a bell curve:
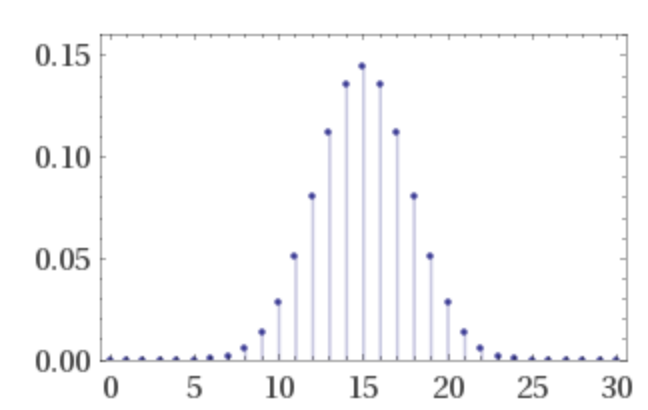 The binomial distribution with 30 coinflips. This already looks a lot like a bell curve!
The binomial distribution with 30 coinflips. This already looks a lot like a bell curve!
Many natural phenomena may also be modeled in this way. For example, the accuracy of measurement instruments (e.g. telescopes) may be viewed as a combination of the manufacturing efficacy of many independent parts, and thus is a good candidate for being modeled via a normal distribution.
The normal distribution is particularly useful in sampling, as the central limit theorem also implies that the distribution of averages of simple random samples is normal. For instance, if we polled many voters on whether they liked (value of 1) or disliked (value of 0) a politician, so long as the voters are independent, the politician's approval rating would be distributed normally regardless of the voters' opinion of them (their opinion would influence the mean and variance of the distribution, but not its shape). This is useful for pollsters, as calculating "margins of error" can be done relatively easily using the empirical rule in the next section.
It is worth noting that not all phenomena are well-modeled by a normal distribution. Even if a phenomenon may be represented as the combination of many factors, if one of those factors outweighs the others, then the distribution will often not be normal.
Student scores on history quizzes are likely to be non-normal since their performance is dominated by whether or not they read the material before class. The distribution is likely to be left-skewed.
Similarly, if the factors are not independent—e.g. if the voters in the above example could hear each others' responses before answering—then normality often breaks down as well.
The 2008 financial crisis was arguably caused by long-term adherence to the assumption that stock prices are normal when, in fact, there is often a herd mentality contributing to swift rises/falls in price. Dependencies among contributing factors lead to distributions with fatter tails than the normal distribution.
In general, these are good rules of thumb to determine whether the normality assumption is appropriate:
| Holds | Fails |
| Amalgamation of similar distributions\(\hspace{15mm}\) | Dominated by one (or few) particular distribution |
| Contributing factors are independent | Dependencies among contributing factors |
| Sample selection is uniformly random | Sample selection is correlated to previous selection |
More formally, there are several statistical tests, most notably Pearson's chi-squared test, to determine whether the normality assumption is valid.
Empirical Rule
The empirical rule, or the 68-95-99.7 rule, states that 68% of the data modeled by a normal distribution falls within 1 standard deviation of the mean, 95% within 2 standard deviations, and 99.7% within 3 standard deviations. For example, IQ is designed to have a mean of 100 and a standard deviation of 15, meaning that 68% of people have IQs between \(100 - 15 = 85\) and \(100 + 15 = 115\), 95% of people have IQs between 70 and 130, and 99.7% of people have IQs between 55 and 145.
This makes the normal distribution easy to obtain quick estimates from, which is especially useful for polling purposes as the margin of error may simply be reported as \(\pm 2\) standard deviations (so, for instance, a candidate's approval rating might be 70% \(\pm\) 3%). For more exact and general calculations, we utilize a \(z\)-score:
The \(z\)-score of an observation is the number of standard deviations away from the mean it is. Formally, if \(\sigma\) is the standard deviation of the distribution, \(\mu\) is the mean of the distribution, and \(x\) is the value, then
\[z = \frac{x - \mu}{\sigma}.\]
For instance, the \(z\)-score of a 121 IQ score is \(\frac{121 - 100}{15} = 1.4\). This value is used in many tests in statistics, most commonly the \(z\)-test. By calculating the area under the bell curve, a \(z\)-score provides the probability of a random variable with this distribution having a value less than the \(z\)-score.
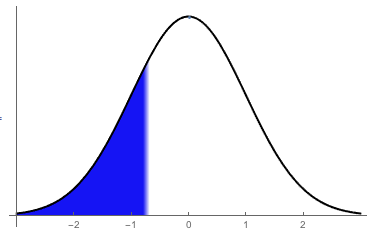 A visual representation of the \(z\)-score \(-0.68\)
A visual representation of the \(z\)-score \(-0.68\)
A \(z\)-score table usually takes the following form, where the column determines the hundredths digit of the \(z\)-score and the row determines the tenths and units digit.
| \(z\) | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
| –3.4 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0002 |
| –3.3 | .0005 | .0005 | .0005 | .0004 | .0004 | .0004 | .0004 | .0004 | .0004 | .0003 |
| –3.2 | .0007 | .0007 | .0006 | .0006 | .0006 | .0006 | .0006 | .0005 | .0005 | .0005 |
| –3.1 | .0010 | .0009 | .0009 | .0009 | .0008 | .0008 | .0008 | .0008 | .0007 | .0007 |
| –3.0 | .0013 | .0013 | .0013 | .0012 | .0012 | .0011 | .0011 | .0011 | .0010 | .0010 |
| –2.9 | .0019 | .0018 | .0018 | .0017 | .0016 | .0016 | .0015 | .0015 | .0014 | .0014 |
| –2.8 | .0026 | .0025 | .0024 | .0023 | .0023 | .0022 | .0021 | .0021 | .0020 | .0019 |
| –2.7 | .0035 | .0034 | .0033 | .0032 | .0031 | .0030 | .0029 | .0028 | .0027 | .0026 |
| –2.6 | .0047 | .0045 | .0044 | .0043 | .0041 | .0040 | .0039 | .0038 | .0037 | .0036 |
| –2.5 | .0062 | .0060 | .0059 | .0057 | .0055 | .0054 | .0052 | .0051 | .0049 | .0048 |
| –2.4 | .0082 | .0080 | .0078 | .0075 | .0073 | .0071 | .0069 | .0068 | .0066 | .0064 |
| –2.3 | .0107 | .0104 | .0102 | .0099 | .0096 | .0094 | .0091 | .0089 | .0087 | .0084 |
| –2.2 | .0139 | .0136 | .0132 | .0129 | .0125 | .0122 | .0119 | .0116 | .0113 | .0110 |
| –2.1 | .0179 | .0174 | .0170 | .0166 | .0162 | .0158 | .0154 | .0150 | .0146 | .0143 |
| –2.0 | .0228 | .0222 | .0217 | .0212 | .0207 | .0202 | .0197 | .0192 | .0188 | .0183 |
| –1.9 | .0287 | .0281 | .0274 | .0268 | .0262 | .0256 | .0250 | .0244 | .0239 | .0233 |
| –1.8 | .0359 | .0351 | .0344 | .0336 | .0329 | .0322 | .0314 | .0307 | .0301 | .0294 |
| –1.7 | .0446 | .0436 | .0427 | .0418 | .0409 | .0401 | .0392 | .0384 | .0375 | .0367 |
| –1.6 | .0548 | .0537 | .0526 | .0516 | .0505 | .0495 | .0485 | .0475 | .0465 | .0455 |
| –1.5 | .0668 | .0655 | .0643 | .0630 | .0618 | .0606 | .0594 | .0582 | .0571 | .0559 |
| –1.4 | .0808 | .0793 | .0778 | .0764 | .0749 | .0735 | .0721 | .0708 | .0694 | .0681 |
| –1.3 | .0968 | .0951 | .0934 | .0918 | .0901 | .0885 | .0869 | .0853 | .0838 | .0823 |
| –1.2 | .1151 | .1131 | .1112 | .1093 | .1075 | .1056 | .1038 | .1020 | .1003 | .0985 |
| –1.1 | .1357 | .1335 | .1314 | .1292 | .1271 | .1251 | .1230 | .1210 | .1190 | .1170 |
| –1.0 | .1587 | .1562 | .1539 | .1515 | .1492 | .1469 | .1446 | .1423 | .1401 | .1379 |
| –0.9 | .1841 | .1814 | .1788 | .1762 | .1736 | .1711 | .1685 | .1660 | .1635 | .1611 |
| –0.8 | .2119 | .2090 | .2061 | .2033 | .2005 | .1977 | .1949 | .1922 | .1894 | .1867 |
| –0.7 | .2420 | .2389 | .2358 | .2327 | .2296 | .2266 | .2236 | .2206 | .2177 | .2148 |
| –0.6 | .2743 | .2709 | .2676 | .2643 | .2611 | .2578 | .2546 | .2514 | .2483 | .2451 |
| –0.5 | .3085 | .3050 | .3015 | .2981 | .2946 | .2912 | .2877 | .2843 | .2810 | .2776 |
| –0.4 | .3446 | .3409 | .3372 | .3336 | .3300 | .3264 | .3228 | .3192 | .3156 | .3121 |
| –0.3 | .3821 | .3783 | .3745 | .3707 | .3669 | .3632 | .3594 | .3557 | .3520 | .3483 |
| –0.2 | .4207 | .4168 | .4129 | .4090 | .4052 | .4013 | .3974 | .3936 | .3897 | .3859 |
| –0.1 | .4602 | .4562 | .4522 | .4483 | .4443 | .4404 | .4364 | .4325 | .4286 | .4247 |
| –0.0 | .5000 | .4960 | .4920 | .4880 | .4840 | .4801 | .4761 | .4721 | .4681 | .4641 |
| 0.1 | .5398 | .5438 | .5478 | .5517 | .5557 | .5596 | .5636 | .5675 | .5714 | .5753 |
| 0.2 | .5793 | .5832 | .5871 | .5910 | .5948 | .5987 | .6026 | .6064 | .6103 | .6141 |
| 0.3 | .6179 | .6217 | .6255 | .6293 | .6331 | .6368 | .6406 | .6443 | .6480 | .6517 |
| 0.4 | .6554 | .6591 | .6628 | .6664 | .6700 | .6736 | .6772 | .6808 | .6844 | .6879 |
| 0.5 | .6915 | .6950 | .6985 | .7019 | .7054 | .7088 | .7123 | .7157 | .7190 | .7224 |
| 0.6 | .7257 | .7291 | .7324 | .7357 | .7389 | .7422 | .7454 | .7486 | .7517 | .7549 |
| 0.7 | .7580 | .7611 | .7642 | .7673 | .7704 | .7734 | .7764 | .7794 | .7823 | .7852 |
| 0.8 | .7881 | .7910 | .7939 | .7967 | .7995 | .8023 | .8051 | .8078 | .8106 | .8133 |
| 0.9 | .8159 | .8186 | .8212 | .8238 | .8264 | .8289 | .8315 | .8340 | .8365 | .8389 |
| 1.0 | .8413 | .8438 | .8461 | .8485 | .8508 | .8531 | .8554 | .8577 | .8599 | .8621 |
Note that the \(z\)-table aligns with the empirical rule. Reading off the table, about \(0.1587\) of the data falls below -1 standard deviation from the mean, and about \(0.8413\) of the data falls below 1 standard deviation from the mean. As a result, about \(0.8413 - 0.1587 = 0.6826 \approx 68\%\) of the data falls between -1 and 1 standard deviations.
Consider a population with a normal distribution that has mean \(3\) and standard deviation \(4\). What is the probability that a value selected at random will be negative? What about positive?
A negative number is any number less than \(0\), so the first step is to find the \(z\)-score associated to \(0\). That is \(\frac{0 - 3}{4} = -0.75\). By finding the row with the first two digits \((-0.7)\) of the \(z\)-score and choosing the column with the next digit \((5),\) we find that the value in the table associated to a value of \(-0.75\) is \(0.2266\), so there is a \(\color{red} \text{22.66%} \) probability that the value will be negative. There is a \(1 - 0.2266 = 0.7734\) or 77.34% probability of it being positive. \(_\square\)
Note that the area under the curve can be computed using integral calculus, so long as the probability density function is known. In particular, if this function is \(f(x)\) and we look at a "standard" normal distribution (i.e. mean 0 and standard deviation 1), then the \(z\)-table entry for a \(z\)-score of \(z\) can be expressed as \(\int_{-\infty}^{z}f(x)\). For instance, the empirical rule can be summarized by
\[\int_{-1}^1 f(x) \approx 68\%,\quad \int_{-2}^2 f(x) \approx 95\%,\quad \int_{-3}^3 f(x) \approx 99.7\%.\]
We will see how to determine \(f(x)\) later.
Properties
The normal distribution has two important properties that make it special as a probability distribution.
The average of \(n\) normal distributions is normal, regardless of \(n\).
There exist other distributions that have this property, and they are called stable distributions. However, the normal distribution is the only stable distribution that is symmetric and has finite variance. Such sums are known as multivariate normal distributions.
Given a simple random sample from a random variable with a normal distribution, the sample mean and sample variance are independent.
This property is unique (among all probability distributions) to the normal distribution. It emphasizes the overall symmetry and "balance" of the bell curve.
Histograms show how samples of a normally distributed random variable approach a bell curve as the sample size increases. The following graphs are of samplings of a random variable with normal distribution of mean \(0\) and standard deviation \(1\).
 \(n = 10\)
\(n = 10\) |
 \(n = 100\)
\(n = 100\) |
 \(n = 1000\)
\(n = 1000\) |
 \(n = 10000\)
\(n = 10000\) |
 \(n = 100000\)
\(n = 100000\) |
 \(n = 1000000\)
\(n = 1000000\) |
Note how the graphs become more and more symmetric as \(n\) increases. The proportion of numbers in a certain region also begins to have a fixed ratio. For instance, as the empirical rule suggests, \(68\%\) of the numbers in the last graph appear between \(-1\) and \(1\). In fact, all normal distributions have these same ratios, and tables of \(z\)-scores are used to determine the exact proportions.
A new product was released and a survey asked customers to give the product a score between 1 and 100. At first, when the number of subjects \((n)\) was still relatively low, the company couldn't pull much information from the surveys. For example, after four people had taken the survey, one person rated it a 92, one rated it a 72, one rated it a 63, and the last one rated it a 34. However, as more customers took the survey, the company was able to create a histogram showing the results. Once 5,000 surveys had been taken, the company found that the average person rated the product a 67 out of 100, and the rest of the scores were normally distributed in a bell-curve out from there (with a standard deviation of 9). Based on this, the company decided that its product was not meeting customers' desires.
Formal Definition and Derivation
The normal distribution with mean \(\mu\) and variance \(\sigma^2\) is denoted \(\mathcal{N}\big(\mu, \sigma^2\big)\). Its probability density function is
\[p_{\mu, \sigma^2} (x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}.\]
There is no closed form expression for the cumulative density function.
If \(X_1\) and \(X_2\) are independent normal random variables, with \(X_1 \sim \mathcal{N}\big(\mu_1, \sigma_1^2\big)\) and \(X_2 \sim \mathcal{N}\big(\mu_2, \sigma_2^2\big)\), then \(aX_1 \pm bX_2 \sim \mathcal{N}\big(a\mu_1 \pm b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2\big)\).
The bell curve is a probability density curve of binary systems. Then the probability at some displacement from the medium is
\[P(n, k) = \left( \begin{matrix} n \\ k \end{matrix} \right) {2}^{-n}= \frac{n!}{\big(\frac{1}{2}n + k\big)!\, \big(\frac{1}{2}n - k\big)!\, {2}^{n}}.\]
Using the Stirling's approximation and treating \(k = \frac{\sigma}{2}\), we have
\[P(n, \sigma) \sim {\left(\frac{n}{2\pi} \right)}^{\frac{1}{2}} {\left(\frac{n}{2}\right)}^{n} {\left(\frac{{n}^{2} - {\sigma}^{2}}{4}\right)}^{-\frac{1}{2}(n+1)}{\left(\frac{n + \sigma}{n-\sigma}\right)}^{\frac{-\sigma}{2}}.\]
For \(n\gg \sigma \), \(\frac{n + \sigma}{n-\sigma} \sim 1+\frac{2\sigma}{n}\); hence, for large \(n\)
\[P(n, \sigma) \sim {\left(\frac{n}{2\pi} \right)}^{\frac{1}{2}} {\left(1- \frac{{\sigma}^{2}}{{n}^{2}}\right)}^{-\frac{1}{2}(n+1)}{\left(1+\frac{2\sigma}{n}\right)}^{\frac{-\sigma}{2}}.\]
Taking the logarithm yields
\[\ln\big(P(n,\sigma)\big) \sim \frac{1}{2}\ln \left (\frac{2}{\pi n}\right) - \frac{1}{2}(n+1)\ln \left (1- \frac{{\sigma}^{2}}{{n}^{2}}\right) - \frac{\sigma}{2}\ln \left (1+\frac{2\sigma}{n}\right).\]
For small \(x\), \(\ln(1+x) \approx x\); subsequently,
\[\ln\big(P(n,\sigma)\big) \sim \frac{1}{2}\ln \left (\frac{2}{\pi n}\right) - \frac{1}{2}(n+1) \left (-\frac{{\sigma}^{2}}{{n}^{2}}\right) - \frac{\sigma}{2} \left (\frac{2\sigma}{n}\right)\]
or
\[\ln\big(P(n,\sigma)\big) \sim \frac{1}{2}\ln \left (\frac{2}{\pi n}\right) + \frac{{\sigma}^{2}}{{n}^{2}} - \frac{{\sigma}^{2}}{2n}.\]
Since \(\frac{{\sigma}^{2}}{{n}^{2}}\) vanishes faster than \(\frac{{\sigma}^{2}}{2n}\) for very large \(n\), we arrive at the result
\[P(n, \sigma) = {\left(\frac{2}{\pi n} \right)}^{\frac{1}{2}} {e}^{\frac{-{\sigma}^{2}}{2n}}.\]