Quadrilateral Classification
A quadrilateral is a four-sided closed figure.The origin of the word "quadrilateral" is the two Latin words quadri, a variant of four, and latus, meaning "side."
Quadrilaterals are simple (not self-intersecting) or complex (self-intersecting), also called crossed. Simple quadrilaterals are either convex or concave.
The sum of all angles of a quadrilateral is always 360˚. This is a special case of the \(n\)-gon interior angle sum formula \((n − 2) \times 180^\circ.\)
Contents
Classification by Sides
Quadrilaterals can be classified on the basis of their sides, giving the following categories:
- Trapezium: no sides the same,
- Isosceles Trapezoid: two opposite sides the same
- Kite: two pairs of sides the same
- Rhombus: all sides the same
Here is an interesting chart, showing family of quadrilaterals:
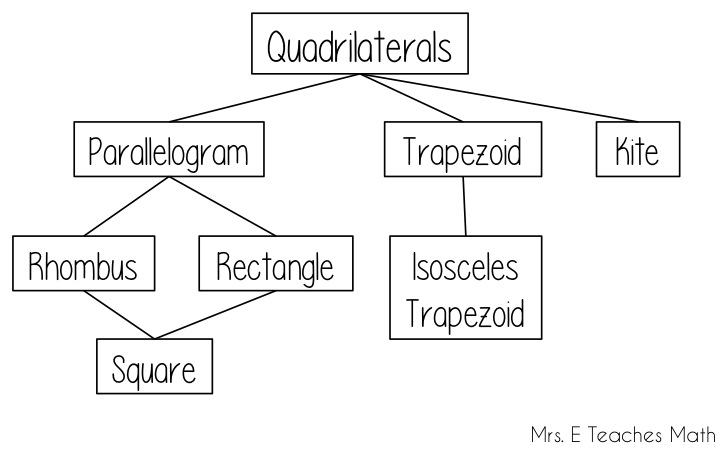
Classification by Angles and Parallels
Quadrilaterals are also commonly classified by their angles and parallel sides:
Parallels
- Trapezoid: one pair of sides parallel
- Parallelogram: both pairs of sides paralllel
Angles
- Rectangle: all angles are right angles (rectangles are always also parallelograms).
Squares
A square, based on the criteria above, is both a rhombus and a rectangle and has all the properties of both of those shapes.
Cyclic Quadrilaterals
A quadrilateral may be cyclic. If opposite angles are supplementary, all its vertices will lie on the circumference a circle, called the circumcircle.