Parallelogram
A parallelogram is a quadrilateral whose opposite sides are parallel.
A parallelogram, in its most general form, looks something like this:
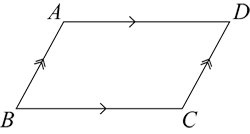 Note that the arrowheads are used to indicate which pair of sides are parallel.
Note that the arrowheads are used to indicate which pair of sides are parallel.
Contents
Special Cases
Basic Properties
Area
Some Cooler Properties
Properties of Parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides.
Properties
The fundamental definition of a parallelogram is as follows:
A parallelogram is a quadrilateral whose opposite sides are parallel.
In the diagram of a general parallelogram above, \( AB || DC \) and \( AD || BC \). Several important properties then follow. First, it is clear that the opposite angles must be equal \(( \angle A = \angle C \) and \( \angle B = \angle D) \) since they make corresponding angles with the two sets of parallel lines. Meanwhile, consecutive angles are supplementary.
Property 1. The opposite angles of a parallelogram are equal.
Property 2. Consecutive angles of a parallelogram are supplementary.
One can also show that the opposite sides are equal \(( AB = DC \) and \( AD = BC): \) the two triangles formed by drawing in a diagonal of the parallelogram \((\)i.e. either the segment \( AC \) or \( BD \) above\()\) must be congruent by angle-side-angle, so the corresponding sides of the two triangles must be congruent as well.
Property 3. The lengths of the opposite sides of a parallelogram are equal.
Now that the lengths of all of the sides are known, it is easy to compute the perimeter of a parallelogram.
Property 4. A parallelogram whose side lengths are \( a \) and \( b \) has perimeter \( 2a + 2 b \).
Meanwhile, the area of the parallelogram can be found by computing the sum of the area of the two triangles formed.
Property 5. The area of a parallelogram with side lengths \( a \) and \( b \), with the acute angle formed between them \( \theta \), is given by \( ab \sin{\theta} \).
Drawing in both diagonals simultaneously produces four congruent triangles. Therefore, the intersection of the two diagonals must be the midpoint of each diagonal.
Property 6. The diagonals of a parallelogram bisect each other.
One last result is left as an exercise for the reader.
Property 7. Lines that connect midpoints of opposite sides with opposite vertices trisect the diagonal.

In the given parallelogram, the midpoints of two adjacent sides of the parallelogram are joined and then connected to the opposite vertex to form a triangle.
What fraction of the total parallelogram is the shaded area?
Click here for more from this set.

A point \(X\) is drawn on the diagonal of a parallelogram \(ABCD\). The lines parallel to the sides through \(X\) are constructed, and quadrilaterals \(P\) and \(Q\) are formed, as shown in the diagram.
Given that \(Q\) has base \(12\) and perpendicular height \(4\) and that the area of \(ABCD\) is \(200\), find the sum of all possible values of the base of \(P\).
Special Parallelograms
Commonly encountered special cases of parallelograms include
- rectangles, all of whose angles are equal;
- rhombuses, all of whose sides are equal;
- squares, all of whose sides and angles are equal.
Because opposite angles of a cyclic quadrilateral are supplementary, all cyclic parallelograms are rectangles. Furthermore, the only rectangles with an incircle are squares, so the only bicyclic parallelogram is a square.
