SAT Triangles

To successfully solve problems about triangles on the SAT, you need to know:

• all triangles on the SAT are non-degenerate
• how to classify triangles by angles and sides
• that the measures of the angles in a triangle add to \(180^\circ\)
• the Triangle Inequality
• about inequalities due to measures of angles and lengths of sides
• how to find the perimeter and area of a triangle

Which of the following list of side lengths can form a triangle?

(A) \(\ \ 1, 2, 1\)
(B) \(\ \ 2, 3, 5\)
(C) \(\ \ 2.6, 2.4, 1\)
(D) \(\ \ 5, 5, 10.5\)
(E) \(\ \ 6, 9, 18\)

---

Correct Answer: C

Solution:

Tip: Triangle Inequality: The sum of the lengths of any two sides in a triangle is greater than the length of its third side.
As shown, (A), (B), (D), and (E) contradict the triangle inequality.

(A) \(1 + 1 \ngtr 2\)
(B) \(2 + 3 \ngtr 5\)
(D) \(5 + 5 \ngtr 10.5\)
(E) \(6 + 9 \ngtr 18\)

Only choice (C) satisfies the triangle inequality. That is,

\[2.6+2.4 > 1, \quad 2.6 + 1 > 2.4,\quad\text{and} \quad 2.4 + 1 > 2.6.\]

---

---

Incorrect Choices:

(A), (B), (D), and (E)
The solutions shows why these choices are wrong.

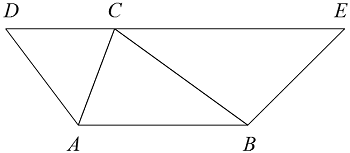
In the figure above \(AB \parallel DE\) and \(CD + CE = 2AB.\) What is the ratio of \(A_{\triangle ABC}\) to \(A_{ABED}?\)

(A) \(\ \ 1:9\)
(B) \(\ \ 1:3\)
(C) \(\ \ 1:2\)
(D) \(\ \ 2:3\)
(E) \(\ \ 3:1\)

---

Correct Answer: B

Solution:

Tip: Area of a triangle with height \(h\) and base \(b\): \(A_{\triangle} = \frac{1}{2}bh.\)
Tip: Know the Properties of Proportions.

\[\begin{array}{r c l l} A_{\triangle ABC} &=& \frac{1}{2} \cdot h \cdot AB &\quad A_{\triangle}=\frac{1}{2}bh\\ \\ A_{ABED} &=& A_{\triangle ACD} + A_{\triangle ABC} + A_{\triangle BCE}&\quad \text{area addition postulate}\\ \\ A_{ABED} &=& \frac{1}{2} \cdot h \cdot CD + \frac{1}{2} \cdot h \cdot AB + \frac{1}{2} \cdot h \cdot CE &\quad A_{\triangle}=\frac{1}{2}bh\\ \\ A_{ABED} &=& \frac{1}{2} \cdot h \cdot (CD + AB + CE) &\quad \text{factor out}\ \frac{1}{2}\cdot h\\ \\ A_{ABED} &=& \frac{1}{2} \cdot h \cdot 3AB &\quad CD + CE = 2AB \\ \\ A_{ABED} &=& \frac{3}{2} \cdot h \cdot AB &\quad \text{re-arrange}\\ \\ \frac{ A_{\triangle ABC} }{ A_{ABED} } &=& \frac{ \frac{1}{2} \cdot h \cdot AB }{ \frac{3}{2} \cdot h \cdot AB } &\quad \text{set up proportion}\\ \\ \frac{ A_{\triangle ABC} }{ A_{ABED} } &=& \frac{1}{3 } &\quad \text{simplify}\\ \\ A_{\triangle ABC} : A_{ABED} &=& 1:3 &\quad \text{re-write}\\ \end{array}\]

---

---

Incorrect Choices:

(A)
You will get this wrong answer if to \(\triangle ABC\) and trapezoid \(ABED\) you apply the theorem which states that if two figures are similar, then the ratio of their areas equals the square of their scale factor. But in this case, we aren't dealing with similar figures.

(C)
Tip: Read the entire question carefully.
This is the ratio of \(AB\) to \(DE,\) not of \(A_{\triangle ABC}\) to \(A_{ABED}. \)

(D)
Tip: Read the entire question carefully.
If you find the ratio \( (A_{\triangle ADC} + A_{\triangle BCE}) : A_{ABED},\) you will get this wrong answer.

(E)
Tip: Read the entire question carefully.
If you find \(A_{ABED} :A_{\triangle ABC} ,\) instead of \(A_{\triangle ABC} : A_{ABED},\) you will get this wrong answer.

If you thought these examples difficult and you need to review the material, these links will help:

• Triangles-Classification by Angles
• Triangles-Classification by Sides
• Triangles-Angle Sum
• Triangles-Exterior Angles
• Properties of Equilateral Triangles
• Properties of Isosceles Triangles
• Triangle Inequality
• Area of a Triangle
• Triangles Problem Solving-Basic
• SAT Lines and Angles
• SAT Parallel Lines

• The angles opposite the two congruent sides in an isosceles triangle are congruent.
• The measures of the angles in a triangle add to \(180^\circ.\)
• The measure of an exterior angle of a triangle equals the sum of the measures of the two non-adjacent interior angles.
• If one side of a triangle is longer than another side, then the angle opposite the first side is bigger than the angle opposite the second side.
• If one angle in a triangle is bigger than another angle, then the side opposite the first angle is longer than the side opposite the second angle.
• Triangle Inequality: The sum of the lengths of any two sides in a triangle is greater than the length of its third side.
• Perimeter of a polygon equals the sum of the lengths of its sides.
• Area of a triangle with height \(h\) and base \(b\): \(A_{\triangle} = \frac{1}{2}bh.\)
• If two triangles have equal heights, then the ratio of their areas equals the ratio of their bases.
• If two triangles have equal bases, then the ratio of their areas equals the ratio of their heights.
• If two figures are similar, and their scale factor is \(a:b,\) then the ratio of their perimeters is \(a:b\) and the ratio of their areas is \(a^2:b^2.\)
• SAT General Tips