Sieve of Eratosthenes

Sieve of Eratosthenes is a simple and ancient algorithm used to find the prime numbers up to any given limit. It is one of the most efficient ways to find small prime numbers.

For a given upper limit $n$ the algorithm works by iteratively marking the multiples of primes as composite, starting from 2. Once all multiples of 2 have been marked composite, the muliples of next prime, ie 3 are marked composite. This process continues until $p\le \sqrt { n }$ where $p$ is a prime number.

Implementation

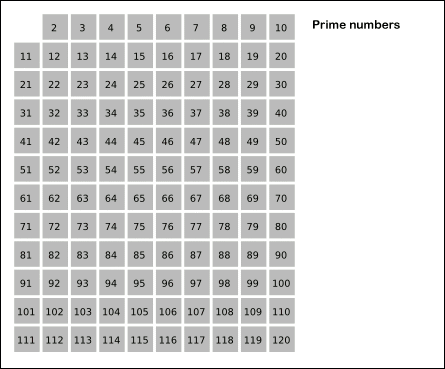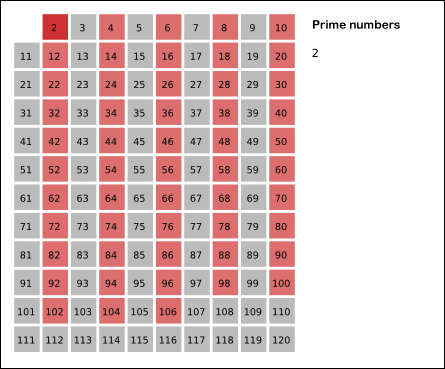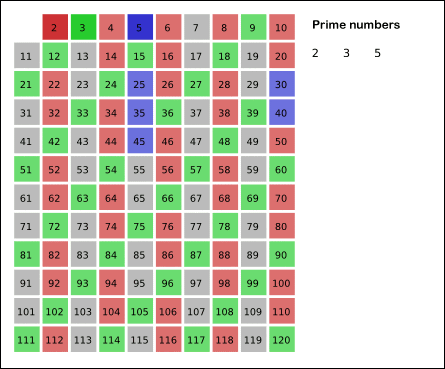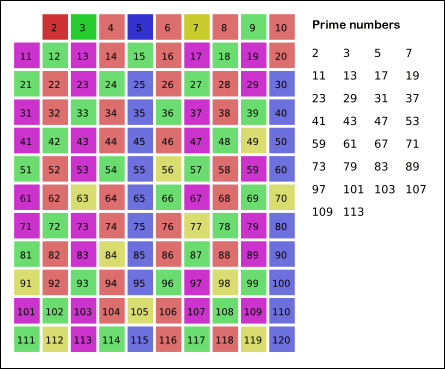Sieve working

In the following algorithm, the number 0 represents a composite number.

To find out all primes under $n$ , generate a list of all integers from 2 to n. (Note: 1 is not prime)
Start with a smallest prime number, ie $p = 2$ .
Mark all the multiples of $p$ which are less than $n$ as composite. To do this, mark the value of the numbers (multiples of $p$ ) in the generated list as 0. Do not mark $p$ itself as composite.
Assign the value of $p$ to the next prime. The next prime is the next non-zero number in the list which is greater than p.
Repeat the process until $p\le \sqrt { n }$ .

We are done!

Now all non-zero numbers in the list represent primes, while the numbers which are 0 in the list represent composite numbers.

Example 1

Generate all the primes less than 11

First thing to note is that do not mark prime themselves as composite.

Create a list of integers from 2 to 10. list = [2, 3, 4, 5, 6, 7, 8, 9, 10]

Start with $p=2$ .

Since $2^2 \le 10$ , continue.

Mark all multiples of 2 as composite by setting their value as 0 in the list. list = [2, 3, 0, 5, 0, 7, 0, 9, 0]

Assign the value of $p$ to the next prime, ie 3.

Since $3^2 \le 10$ , continue.

Mark all multiples of 3 as composite by setting their value as 0 in the list. list = [2, 3, 0, 5, 0, 7, 0, 0, 0]

Assign the value of $p$ to 5.

Since $5^{ 2 }\nleq 10$ , stop.

We are done!

The list is [2, 3, 0, 5, 0, 7, 0, 0, 0]. Since all the numbers which are 0 are composite, all the non-zero numbers are prime. Hence the prime numbers less 11 are 2, 3, 5, 7. $_\square$

Example 2

Generate all the primes less than any integer $n$

Since $n$ could be any large number, manually computing the answer would take years. Let's write a code for this.

import math

n = 200 # n is any arbitrary integer
List = []

for x in xrange(2, n): # add numbers from 2 to n - 1 to List
    List.append(x)
# note the above statement is equivalent to List = range(2, n)

p = 2 # p is a prime

while not int(math.sqrt(p)) + 1 > n: # continue to mark out primes until square root of p is less than n

    for x in xrange(p * 2, n, p): # remove all the multiples of p
        List[x - 2] = 0

    p += 1

    while p - 2 < len(List) and List[p - 2] == 0: # assign p to the next prime. Next prime is the next non zero number in the list
        p += 1

for x in List: # search for non zero or prime numbers in the list and print them
    if x != 0:
        print x

Here is an optimized java version -

final int lim = 200; // exclusive

int n[] = new int[lim - 2]; //exclude 1
for(int i = 2; i <= lim - 1; i++) //initialize the array with integers from 2 to lim
{
  if((i & 1) == 0) //evens are not primes f & 1 return 0 if f % 2 == 0
  {
    n[i - 2] = 0;
  }
  else
  {
    n[i - 2] = i;
  }
}

n[0] = 2;

int p = 3; //start with a prime. Since 2 is already eliminated, start with 3

while(p * p < lim)
{
  for(int i = p * p; i < lim; i += p + p) //remvove multiples of prime. Start at p * p
  {
    n[i - 2] = 0;
  }

  while(n[(p += 2) - 2] == 0) //find next non zero number. This is guaranteed to be a prime.
    ;
}

for(int i = 0; i < lim - 2; i++) //print non zero numbers
{
  if(n[i] != 0)
  {
    System.out.println(n[i]);
  }
}

Proof: To see why Sieve of Eratosthenes generates all the primes

To first understand why the sieve works, let's look into the definitions of prime decomposition and composite numbers.

Theorem 1

Every integer which is greater than 1 can be expressed as product of primes.

Theorem 2

If any integer $n$ is composite, then $n$ has a prime divisor less than or equal to $\sqrt { n }$ .

Since for any number $n$ in the list, we are looking all prime numbers up to $\sqrt { n }$ , we are indeed separating all composite numbers. Hence Sieve of Eratosthenes generates all primes numbers less than the upper limit. $_\square$